Engage NY Eureka Math 7th Grade Module 2 Lesson 7 Answer Key
Eureka Math Grade 7 Module 2 Lesson 7 Example Answer Key
Example 1.
Representing Sums of Rational Numbers on a Number Line
a. Place the tail of the arrow on 12.
b. The length of the arrow is the absolute value of -3\(\frac{1}{2}\) , |-3 \(\frac{1}{2}\) | = 3 \(\frac{1}{2}\) .
c. The direction of the arrow is to the left since you are adding a negative number to 12.
Draw the number line model in the space below.

Answer:

12 + ( -3\(\frac{1}{2}\) ) = 8\(\frac{1}{2}\) or 12 – 3\(\frac{1}{2}\) = 8\(\frac{1}{2}\)
Example 2.
Representing Differences of Rational Numbers on a Number Line
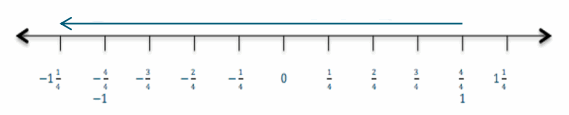
Find the following difference, and represent it on a number line: 1 – 2\(\frac{1}{4}\) .
a.
Answer:
Rewrite the difference 1 – 2\(\frac{1}{4}\) as a sum: 1 + (-2 \(\frac{1}{4}\)).
Now follow the steps to represent the sum:
b.
Answer:
Place the tail of the arrow on 1.
c.
Answer:
The length of the arrow is the absolute value of -2 \(\frac{1}{4}\) ; | -2 \(\frac{1}{4}\) |= 2\(\frac{1}{4}\) .
d.
Answer:
The direction of the arrow is to the left since you are adding a negative number to 1.
Draw the number line model in the space below.

Answer:
Eureka Math Grade 7 Module 2 Lesson 7 Exercise Answer Key
Exercise 1.
Real-World Connection to Adding and Subtracting Rational Numbers
Suppose a seventh grader’s birthday is today, and she is 12 years old. How old was she 3\(\frac{1}{2}\) years ago? Write an equation, and use a number line to model your answer.
Answer:
12 + ( -3\(\frac{1}{2}\)) = 8\(\frac{1}{2}\) or 12 – 3\(\frac{1}{2}\) = 8\(\frac{1}{2}\)

Exercise 2.
Find the following sum using a number line diagram: -2\(\frac{1}{2}\) + 5.
Answer:

(-2\(\frac{1}{2}\)) + 5 = 2\(\frac{1}{2}\)
Exercise 3.
Find the following difference, and represent it on a number line: -5\(\frac{1}{2}\) – (-8).
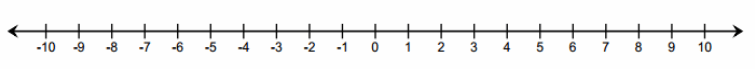
Answer:

(-5\(\frac{1}{2}\) ) + 8 = 2 \(\frac{1}{2}\)
Exercise 4.
Find the following sums and differences using a number line model.
a. -6 + 5\(\frac{1}{4}\)
Answer:
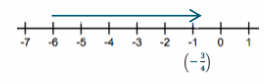
-6 + 5 \(\frac{1}{4}\) = –\(\frac{3}{4}\)
b. 7-(-0.9)
Answer:
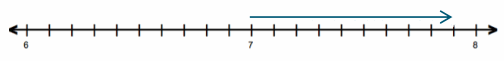
7 + (0.9) = 7.9
c. 2.5 + (-\(\frac{1}{2}\) )
Answer:
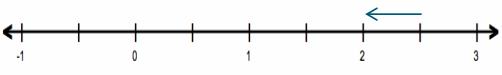
2.5 + (-0.5) = 2
d. –\(\frac{1}{4}\) + 4
Answer:
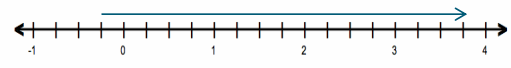
–\(\frac{1}{4}\) + 4 = 3\(\frac{3}{4}\)
e. –\(\frac{1}{2}\) – (-3)
Answer:
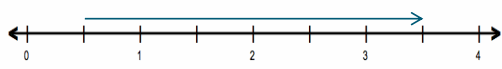
\(\frac{1}{2}\) + 3 = 3 \(\frac{1}{2}\)
Exercise 5.
Create an equation and number line diagram to model each answer.
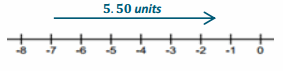
a. Samantha owes her father $7. She just got paid $5.50 for babysitting. If she gives that money to her dad, how much will she still owe him?
Answer:
-7 + 5.50 = -1.50. She still owes him $1.50.
b. At the start of a trip, a car’s gas tank contains 12 gallons of gasoline. During the trip, the car consumes 10\(\frac{1}{8}\) gallons of gasoline. How much gasoline is left in the tank?
Answer:
12 + (-10\(\frac{1}{8}\) ) = 1\(\frac{7}{8}\) or 12-10\(\frac{1}{8}\) =1 \(\frac{7}{8}\) ,There are 1\(\frac{7}{8}\) gallons of gas left in the tank.

c. A fish was swimming 3\(\frac{1}{2}\) feet below the water’s surface at 7:00 a.m. Four hours later, the fish was at a depth that is 5\(\frac{1}{4}\) feet below where it was at 7:00 a.m. What rational number represents the position of the fish with respect to the water’s surface at 11:00 a.m.?
Answer:
-3\(\frac{1}{2}\) +(-5\(\frac{1}{4}\) )= -8\(\frac{3}{4}\) . The fish is 8\(\frac{3}{4}\) feet below the water’s surface.
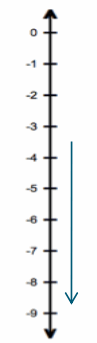
Eureka Math Grade 7 Module 2 Lesson 7 Problem Set Answer Key
Represent each of the following problems using both a number line diagram and an equation.
Question 1.
A bird that was perched atop a 15\(\frac{1}{2}\) -foot tree dives down six feet to a branch below. How far above the ground is the bird’s new location?
Answer:
15\(\frac{1}{2}\) + (-6) = 9\(\frac{1}{2}\)
The bird is 9\(\frac{1}{2}\) feet above the ground.
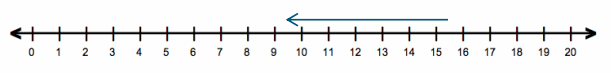
Question 2.
Mariah owed her grandfather $2.25 but was recently able to pay him back $1.50. How much does Mariah currently owe her grandfather?
Answer:
-2.25 + 1.50 = -0.75
Mariah owes her grandfather 75 cents.
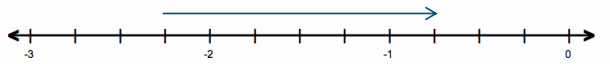
Question 3.
Jake is hiking a trail that leads to the top of a canyon. The trail is 4.2 miles long, and Jake plans to stop for lunch after he completes 1.6 miles. How far from the top of the canyon will Jake be when he stops for lunch?
Answer:
4.2 – 1.6 = 2.6
Jake will be 2.6 miles from the top of the canyon.
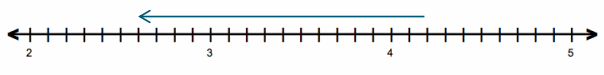
Question 4.
Sonji and her friend Rachel are competing in a running race. When Sonji is 0.4 miles from the finish line, she notices that her friend Rachel has fallen. If Sonji runs one-tenth of a mile back to help her friend, how far will she be from the finish line?
Answer:
-0.4 + (-0.1) = -0.5 or -0.4 – 0.1 = -0.5
Sonji will be 0.5 miles from the finish line.
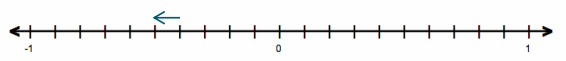
Question 5.
Mr. Henderson did not realize his checking account had a balance of $200 when he used his debit card for a $317.25 purchase. What is his checking account balance after the purchase?
Answer:
200 + (-317.25) = -117.25 or 200 – 317.25 = -117.25
Mr. Henderson’s checking account balance will be -$117.25.
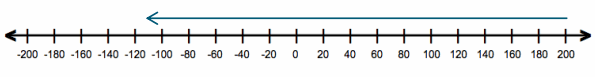
Question 6.
If the temperature is -3°F at 10:00 p.m., and the temperature falls four degrees overnight, what is the resulting temperature?
Answer:
-3 – 4 = -3 + (-4) = -7
The resulting temperature is -7°F.
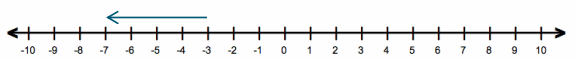
Eureka Math Grade 7 Module 2 Lesson 7 Exit Ticket Answer Key
At the beginning of the summer, the water level of a pond is 2 feet below its normal level. After an unusually dry summer, the water level of the pond dropped another 1\(\frac{1}{3}\) feet.
Question 1.
Use a number line diagram to model the pond’s current water level in relation to its normal water level.
Answer:
Move 1\(\frac{1}{3}\) units to the left of -2. -3\(\frac{1}{3}\)
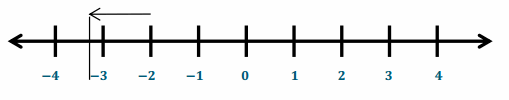
Question 2.
Write an equation to show how far above or below the normal water level the pond is at the end of the summer.
Answer:
-2 – 1\(\frac{1}{3}\) = -3\(\frac{1}{3}\) or -2 + (-1\(\frac{1}{3}\)) = -3\(\frac{1}{3}\)