Engage NY Eureka Math 7th Grade Module 2 Lesson 6 Answer Key
Eureka Math Grade 7 Module 2 Lesson 6 Example Answer Key
Example 1.
Formula for the Distance Between Two Rational Numbers
Find the distance between -3 and 2.
Step 1: Start on an endpoint.
Step 2: Count the number of units from the endpoint you started on to the other endpoint.
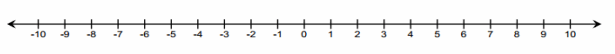
Answer:

Using a formula, _____
Answer:
| -3 – 2 | = | -3 + -2 | = | -5 | = 5 OR | 2 – (-3) | = | 2 + 3 | = | 5 | = 5
For two rational numbers p and q, the distance between p and q is |p – q|.
Example 2.
Change in Elevation vs. Distance
Distance is positive. Change in elevation or temperature may be positive or negative depending on whether it is increasing or decreasing (going up or down).
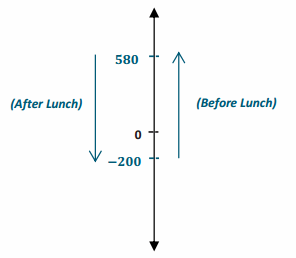
a. A hiker starts hiking at the beginning of a trail at a point which is 200 feet below sea level. He hikes to a location on the trail that is 580 feet above sea level and stops for lunch.
i. What is the vertical distance between 200 feet below sea level and 580 feet above sea level?
Answer:
| -200 – 580 | = | -200 + (-580) | = | -780 | = 780
The vertical distance is 780 feet.
ii. How should we interpret 780 feet in the context of this problem?
Answer:
The hiker hiked 780 feet from a point below sea level to a point above sea level.
b. After lunch, the hiker hiked back down the trail from the point of elevation, which is 580 feet above sea level, to the beginning of the trail, which is 200 feet below sea level.
Answer:
i. What is the vertical distance between 580 feet above sea level and 200 feet below sea level?
Answer:
| 580 – (-200) | = | 580 + 200 | = | 780 | = 780
The vertical distance is 780 feet.
ii. What is the change in elevation?
Answer:
780 feet
Eureka Math Grade 7 Module 2 Lesson 6 Exercise Answer Key
Exercise 1.
Use the number line to answer each of the following.

Answer:
Exercise 2.
Use the number line to answer each of the following questions.
a. What is the distance between 0 and -8?
Answer:
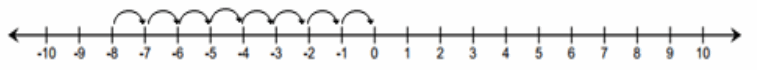
| 0 – (-8) | = | 0 + 8| = |8| = 8
b. What is the distance between -2 and –1\(\frac{1}{2}\)?
Answer:
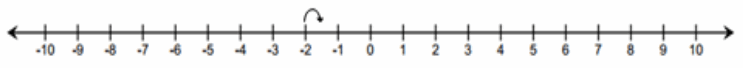
| – 2 – (-1 \(\frac{1}{2}\) )|=| -2 + 1 \(\frac{1}{2}\) |=|-\(\frac{1}{2}\) | = \(\frac{1}{2}\)
c. What is the distance between -6 and -10?
Answer:
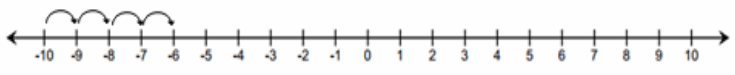
| -6 – (-10) | = | -6 + 10 | = | 4 | = 4
Exercise 3.
The distance between a negative number and a positive number is 12\(\frac{1}{2}\). What are the numbers?
Answer:
Answers will vary; a possible solution is -9\(\frac{1}{2}\) and 3. |-9\(\frac{1}{2}\) – 3 | = | -9\(\frac{1}{2}\) + (- 3) | = |-12\(\frac{1}{2}\)| = 12\(\frac{1}{2}\)
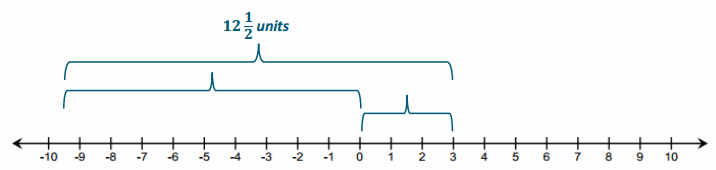
| -9\(\frac{1}{2}\) | = 9\(\frac{1}{2}\) | 3 | = 3
Exercise 4.
Use the distance formula to find each answer. Support your answer using a number line diagram.
a. Find the distance between -7 and -4.
Answer:
| -7 – (-4) | = | -7 + 4 | = | -3 | = 3
The distance between -7 and -4 is 3 units.
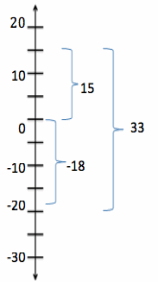
b. Find the change in temperature if the temperature rises from -18°F to 15°F (use a vertical number line).
Answer:
| 15 – (-18) | = | 15 + 18 | = | 33 | = 33
The change in temperature is 33°F.
c. Would your answer for part (b) be different if the temperature dropped from 15°F to -18°F? Explain.
Answer:
Yes. The distance between 15 and -18 on a number line is the same as the distance between -18 and 15 because the endpoints are the same, but the temperature would change by -33°F because it is going from a higher value to a lower value.
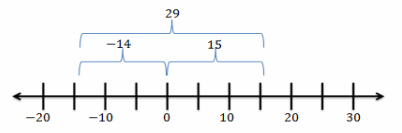
d. Beryl is the first person to finish a 5K race and is standing 15 feet beyond the finish line. Another runner, Jeremy, is currently trying to finish the race and has approximately 14 feet before he reaches the finish line. What is the minimum possible distance between Beryl and Jeremy?
Answer:
| -14 – 15 | = | -14 + (-15) | = | -29 | = 29
The minimum distance between Beryl and Jeremy is 29 feet.
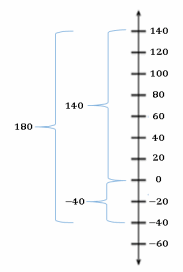
e. What is the change in elevation from 140 feet above sea level to 40 feet below sea level? Explain.
Answer:
I used the distance formula: | 140 – (-40) | = 180 and a vertical number line to find the distance between the two elevations. However, the elevation is going from a higher elevation to a lower one, so the change would be negative. Therefore, the change in elevation is -180 feet.
Eureka Math Grade 7 Module 2 Lesson 6 Problem Set Answer Key
Question 1.
| -19 – 12 |
Answer:
| -19 – 12 | = | -19 + (-12) | = |-31| = 31
Question 2.
| 19 – (-12) |
Answer:
| 19 – (-12) | = | 19 + 12 | = | 31 | = 31
Question 3.
| 10 – (-43) |
Answer:
| 10 – (-43) | = | 10 + 43 | = | 53 | = 53
Question 4.
| – 10 – 43 |
Answer:
| – 10 – 43 | = | -10 + (-43) | = | -53 | = 53
Question 5.
| -1 – (-16) |
Answer:
| -1 – (-16) | = | -1 + 16 |= | 15 | = 15
Question 6.
| 1 – 16 |
Answer:
| 1 – 16 | = | 1 + (-16) | = | -15 | = 15
Question 7.
| 0 – (-9) |
Answer:
| 0 – (-9) | = | 0 + 9 | = | 9 | = 9
Question 8.
| 0 – 9|
Answer:
| 0 – 9| = | 0 + (-9) | = | -9 | = 9
Question 9.
| -14.5 – 13 |
Answer:
| -14.5 – 13 | = | -14.5 + (-13) | = | -27.5 | = 27.5
Question 10.
| 14.5 – (-13) |
Answer:
| 14.5 – (-13) | = | 14.5 + 13 | = |27.5| = 27.5
Question 11.
Describe any patterns you see in the answers to the problems in the left- and right-hand columns. Why do you think this pattern exists?
Answer:
Each problem in the right-hand column has the same answer as the problem across from it in the left-hand column. That is because you are finding the distance between the opposite numbers as compared to the first column. The difference between the opposite numbers is opposite the difference between the original numbers. The absolute values of opposite numbers are the same.
Eureka Math Grade 7 Module 2 Lesson 6 Exit Ticket Answer Key
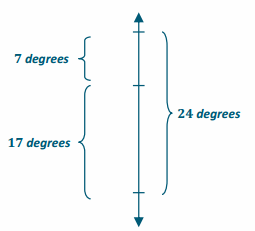
Two Grade 7 students, Monique and Matt, both solved the following math problem:
If the temperature drops from 7°F to -17°F, by how much did the temperature decrease?
The students came up with different answers. Monique said the answer is 24°F, and Matt said the answer is 10°F. Who is correct? Explain, and support your written response with the use of a formula and a vertical number line diagram.
Answer:
Monique is correct. If you use the distance formula, you take the absolute value of the difference between 7 and -17 and that equals 24. Using a number line diagram, you can count the number of units between 7 and -17 to get 24.
| 7 – (-17) | = | 7 + 17 | = | 24 | = 24. There was a 24°F drop in the temperature.