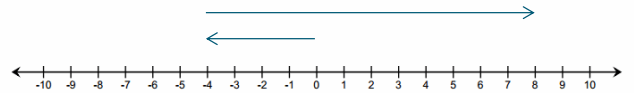Engage NY Eureka Math 7th Grade Module 2 Lesson 3 Answer Key
Eureka Math Grade 7 Module 2 Lesson 3 Example Answer Key
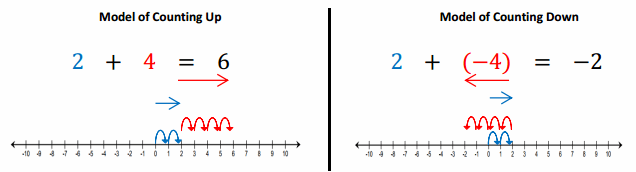
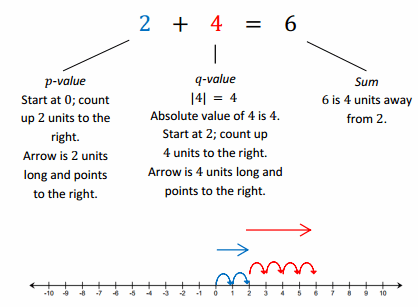
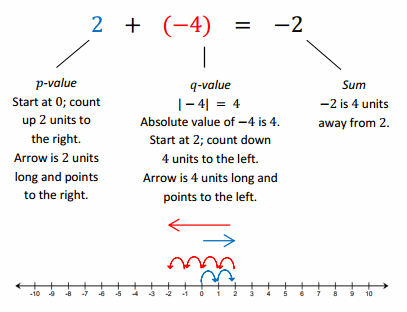
Example 1.
Counting On to Express the Sum as Absolute Value on a Number Line
Horizontal Number Line Model of Counting Up
Horizontal Number Line Model of Counting Down
Vertical Number Line Model of Counting Up
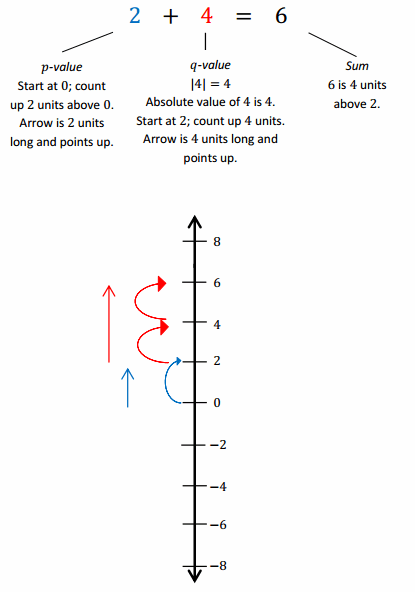
Vertical Number Line Model of Counting Down
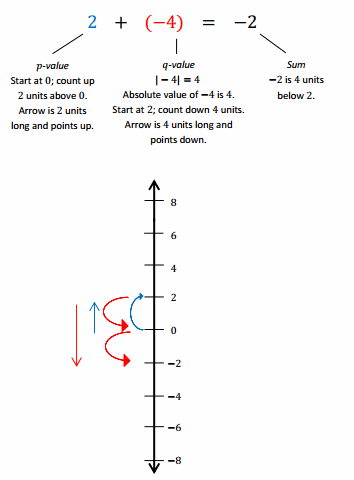
Counting up -4 is the same as the opposite of counting up 4 and also means counting down 4.
a. For each example above, what is the distance between 2 and the sum?
Answer:
4 units
b. Does the sum lie to the right or left of 2 on a horizontal number line? Above or below on a vertical number line?
Answer:
Horizontal: On the first model, the sum lies to the right of 2. On the second model, it lies to the left of 2.
Vertical: On the first model, the sum lies above 2. On the second model, it lies below 2.
c. Given the expression 54+81, determine, without finding the sum, the distance between 54 and the sum. Explain.
Answer:
The distance will be 81 units. When the q-value is positive, the sum will be to the right of (or above) the p-value the same number of units as the q-value.
d. Is the sum to the right or left of 54 on the horizontal number line? Above or below on a vertical number line?
Answer:
The sum is to the right of 54 on a horizontal number line and above 54 on a vertical number line.
e. Given the expression 14 + (-3), determine, without finding the sum, the distance between 14 and the sum. Explain.
Answer:
The distance will be 3 units. When the q-value is negative, the sum will be to the left of (or below) the p-value the same number of units as the q-value.
f. Is the sum to the right or left of 14 on the number line? Above or below on a vertical number line?
Answer:
The sum is to the left of 14 on a horizontal number line and below 14 on a vertical number line.
Eureka Math Grade 7 Module 2 Lesson 3 Exercise Answer Key
Exercise 2
Work with a partner to create a horizontal number line model to represent each of the following expressions. What is the sum?
a. -5 + 3
Answer:
-5 + 3 = -2. The sum is 3 units to the right of -5.
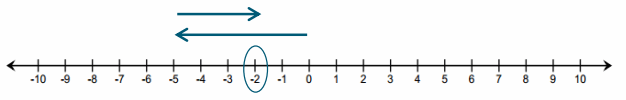
b. -6 + (-2)
Answer:
-6 + (-2) = -8. The sum is 2 units to the left of -6.
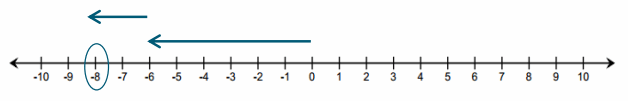
c. 7 + (-8)
Answer:
7 + (-8) = -1. The sum is 8 units to the left of 7.
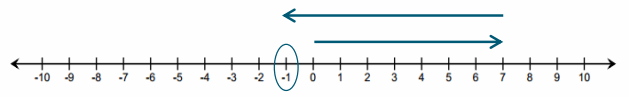
Exercise 3.
Writing an Equation Using Verbal Descriptions
Write an equation, and using the number line, create an arrow diagram given the following information:
The sum of 6 and a number is 15 units to the left of 6 on the number line.
Answer:
Eureka Math Grade 7 Module 2 Lesson 3 Exit Ticket Answer Key
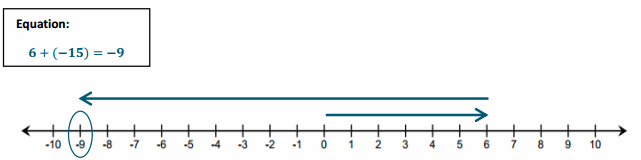
Question 1.
Refer to the diagram to the right.
a. Write an equation for the diagram below.
Answer:
-5 + (-4) = -9
b. Find the sum.
Answer:
-9

c. Describe the sum in terms of the distance from the first addend. Explain.
Answer:
The sum is 4 units below -5 because |-4| = 4. I counted down from -5 four times and stopped at -9.
d. What integers do the arrows represent?
Answer:
The arrows represent the integers -4 and -5.
Question 2.
Jenna and Jay are playing the Integer Game. Below are the two cards they selected.
a. How do the models for these two addition problems differ on a number line? How are they the same?
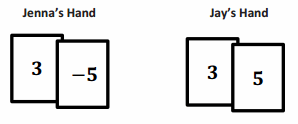
Answer:
The p-values are the same. They are both 3, so the heads of the first arrows will be at the same point on the number line. The sums will both be five units from this point but in opposite directions.
b. If the order of the cards changed, how do the models for these two addition problems differ on a number line? How are they the same?
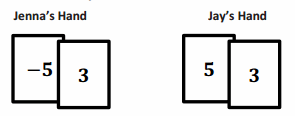
Answer:
The first addends are different, so the head of the first arrow in each model will be at different points on the number line. The sums are both three units to the right of the first addend.
Eureka Math Grade 7 Module 2 Lesson 3 Problem Set Answer Key
Question 1.
Below is a table showing the change in temperature from morning to afternoon for one week.
a. Use the vertical number line to help you complete the table. As an example, the first row is completed for you.
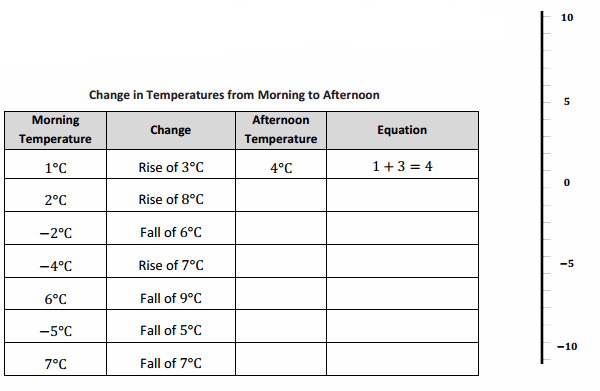
Answer:
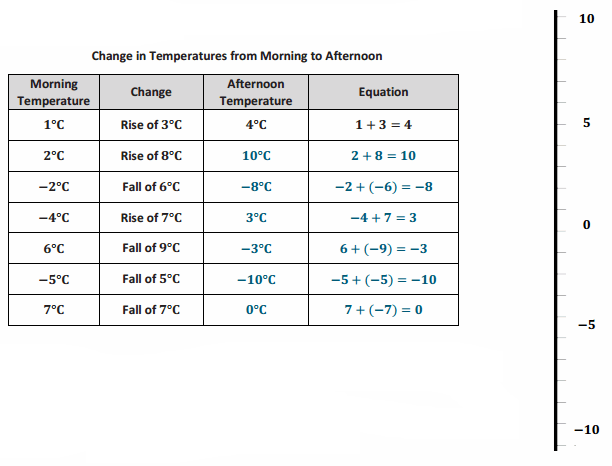
b. Do you agree or disagree with the following statement: “A rise of -7°C” means “a fall of 7°C?” Explain. (Note: No one would ever say, “A rise of -7 degrees”; however, mathematically speaking, it is an equivalent phrase.)
Answer:
Sample response: I agree with this statement because a rise of -7 is the opposite of a rise
of 7. The opposite of a rise of 7 is a fall of 7.
For Problems 2–3, refer to the Integer Game.
Question 2.
Terry selected two cards. The sum of her cards is -10.
a. Can both cards be positive? Explain why or why not.
Answer:
No. In order for the sum to be -10, at least one of the addends would have to be negative. If both cards are positive, then Terry would count up twice going to the right. Negative integers are to the left of 0.
b. Can one of the cards be positive and the other be negative? Explain why or why not.
Answer:
Yes. Since both cards cannot be positive, this means that one can be positive and the other negative.
She could have -11 and 1 or -12 and 2. The card with the greatest absolute value would have to be negative.
c. Can both cards be negative? Explain why or why not.
Answer:
Yes, both cards could be negative. She could have -8 and -2. On a number line, the sum of two negative integers will be to the left of 0.
Question 3.
When playing the Integer Game, the first two cards you selected were -8 and -10.
a. What is the value of your hand? Write an equation to justify your answer.
Answer:
-8 + (-10) = -18
b. For part (a), what is the distance of the sum from -8? Does the sum lie to the right or left of -8 on the number line?
Answer:
The distance is 10 units from -8, and it lies to the left of -8 on the number line.
c. If you discarded the -10 and then selected a 10, what would be the value of your hand? Write an equation to justify your answer.
Answer:
The value of the hand would be 2. -8+10=2.
Question 4.
Given the expression 67+(-35), can you determine, without finding the sum, the distance between 67 and the sum? Is the sum to the right or left of 67 on the number line?
Answer:
The distance would be 35 units from 67. The sum is to the left of 67 on the number line.
Question 5.
Use the information given below to write an equation. Then create an arrow diagram of this equation on the number line provided below.
Answer:
The sum of -4 and a number is 12 units to the right of -4 on a number line.
-4 + 12 = 8