Engage NY Eureka Math 7th Grade Module 2 Lesson 22 Answer Key
Eureka Math Grade 7 Module 2 Lesson 22 Example Answer Key
Example 1.
Yoshiro’s New Puppy
Yoshiro has a new puppy. She decides to create an enclosure for her puppy in her backyard. The enclosure is in the shape of a hexagon (six-sided polygon) with one pair of opposite sides running the same distance along the length of two parallel flower beds. There are two boundaries at one end of the flower beds that are 10 ft. and 12 ft., respectively, and at the other end, the two boundaries are 15 ft. and 20 ft., respectively. If the perimeter of the enclosure is 137 ft., what is the length of each side that runs along the flower bed?
→ What is the general shape of the puppy yard? Draw a sketch of the puppy yard.
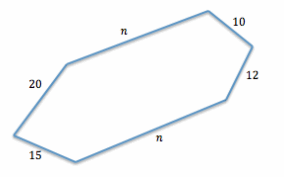
→ Write an equation that would model finding the perimeter of the puppy yard.
→ The sum of the lengths of the sides = Perimeter
n + n + 10 + 12 + 20 + 15 = 137
→ Model and solve this equation with a tape diagram.
→ Sample response:
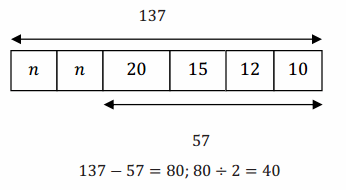
→ Now review making zero in an equation and making one in an equation. Explicitly connect making zero and making one in the next question to the bar model diagram. Subtracting 57 from 137 in the bar diagram is the same as using the subtraction property of equality (i.e., subtracting 57 from both sides of the equation in order to make zero). Dividing 80 by 2 to find the size of two equal groups that total 80 is the same as using the multiplicative property of equality (i.e., multiplying each side of the equation by \(\frac{1}{2}\) to make one group of n).
→ Use algebra to solve this equation.
→ First, use the additive inverse to find out what the lengths of the two missing sides are together. Then, use the multiplicative inverse to find the length of one of the two equal sides. Sum of missing sides + Sum of known sides = Perimeter
If: 2n + 57 = 137
Then: 2n + 57-57 = 137-57 Subtraction property of equality
If: 2n + 0 = 80
Then: 2n = 80 Additive identity
If: 2n = 80
Then: \(\frac{1}{2}\) (2n) = \(\frac{1}{2}\)(80) Multiplication property of equality
If: 1n = 40
Then: n = 40 Multiplicative identity
→ Does your solution make sense in this context? Why?
→ Yes, 40 ft. makes sense because when you replace the two missing sides of the hexagon with 40 in the number sentence ( 40 + 40 + 10 + 12 + 20 + 15 = 137), the lengths of the sides reach a total of 137.
Example 2.
Swim Practice
Jenny is on the local swim team for the summer and has swim practice four days per week. The schedule is the same each day. The team swims in the morning and then again for 2 hours in the evening. If she swims 12 hours per week, how long does she swim each morning?
Answer:
→ Write an algebraic equation to model this problem. Draw a tape diagram to model this problem.
→ Let x = number of hours of swimming each morning
Model days per week (number of hours swimming a.m. and p.m.) = hours of swimming total
![]()
Recall in the last problem that students used making zero first and then making one to solve the equation. Explicitly connect making zero and making one in the previous statement to the tape diagram.
→ Solve the equations algebraically and graphically with the help of the tape diagram.
→ Sample response:

→ Does your solution make sense in this context? Why?
→ Yes, if Jenny swims 1 hour in the morning and 2 hours in the evening for a total of 3 hours per day and swims 4 days per week, then 3(4) = 12 hours for the entire week.
Eureka Math Grade 7 Module 2 Lesson 22 Exercise Answer Key
Solve each equation algebraically using if–then statements to justify each step.
Question 1.
5x + 4 = 19
Answer:
If: 5x + 4 = 19
Then: 5x + 4-4 = 19-4 Subtraction property of equality for the additive inverse of 4
If: 5x + 0 = 15
Then: 5x = 15 Additive identity
If: 5x = 15
Then: \(\frac{1}{5}\) (5x) = (\(\frac{1}{5}\))15 Multiplication property of equality for the multiplicative inverse of 5
If: 1x = 3
Then: x = 3 Multiplicative identity
Question 2.
15x + 14 = 19
Answer:
If: 15x + 14 = 19
Then: 15x + 14-14 = 19-14 Subtraction property of equality for the additive inverse of 14
If: 15x + 0 = 5
Then: 15x = 5 Additive Identity
If: 15x = 5
Then: \(\frac{1}{15}\) (15x) = (\(\frac{1}{15}\))5 Multiplication property of equality for the multiplicative inverse of 15
If: 1x = \(\frac{1}{3}\)
Then: x = \(\frac{1}{3}\) Multiplicative identity
Question 3.
Claire’s mom found a very good price on a large computer monitor. She paid $325 for a monitor that was only $65 more than half the original price. What was the original price?
Answer:
x: the original price of the monitor
If: \(\frac{1}{2}\) x + 65 = 325
Then: \(\frac{1}{2}\) x + 65-65 = 325-65 Subtraction property of equality for the additive inverse of 65
If: \(\frac{1}{2}\) x + 0 = 260
Then: \(\frac{1}{2}\) x = 260 Additive identity
If: \(\frac{1}{2}\) x = 260
Then: (2)\(\frac{1}{2}\) x = (2)260 Multiplication property of equality for the multiplicative inverse of \(\frac{1}{2}\)
If: 1x = 520
Then: x = 520 Multiplicative identity
The original price was $520.
Question 4.
2(x + 4) = 18
Answer:
If: 2(x + 4) = 18
Then: \(\frac{1}{2}\) (2 (x + 4)) = \(\frac{1}{2}\) (18) Multiplication property of equality using the multiplicative inverse of 2
If: 1(x + 4) = 9
Then: x + 4 = 9 Multiplicative identity
If: x + 4 = 9
Then: x + 4-4 = 9-4 Subtraction property of equality for the additive inverse of 4
If: x + 0 = 5
Then: x = 5 Additive identity
Question 5.
Ben’s family left for vacation after his dad came home from work on Friday. The entire trip was 600 mi. Dad was very tired after working a long day and decided to stop and spend the night in a hotel after 4 hours of driving. The next morning, Dad drove the remainder of the trip. If the average speed of the car was 60 miles per hour, what was the remaining time left to drive on the second part of the trip? Remember: Distance = rate multiplied by time.
Answer:
m: the number of miles driven on the second day
60 (m + 4) = 600
If: 60 (m + 4) = 600
Then: (\(\frac{1}{60}\))60 (m + 4) = (\(\frac{1}{60}\))600 Multiplication property of equality for the multiplicative inverse of 60
If: 1 ( m + 4) = 10
Then: m + 4 = 10 Multiplicative identity
If: m + 4 = 10
Then: m + 4-4 = 10-4 Subtraction property of equality for the additive inverse of 4
If: m + 0 = 6
Then: m = 6 Additive identity
There were 6 hours left to drive.
Eureka Math Grade 7 Module 2 Lesson 22 Problem Set Answer Key
For each problem below, explain the steps in finding the value of the variable. Then find the value of the variable, showing each step. Write if–then statements to justify each step in solving the equation.
Question 1.
7(m + 5) = 21
Answer:
Multiply both sides of the equation by \(\frac{1}{7}\) , and then subtract 5 from both sides of the equation; m = -2.
If: 7(m + 5) = 21
Then: \(\frac{1}{7}\) (7(m + 5)) = \(\frac{1}{7}\) (21) Multiplication property of equality using the multiplicative inverse of 7
If: 1 (m + 5) = 3
Then: m + 5 = 3 Multiplicative identity
If: m + 5 = 3
Then: m + 5-5 = 3-5 Subtraction property of equality for the additive inverse of 5
If: m + 0 = -2
Then: m = -2 Additive identity
Question 2.
-2v + 9 = 25
Answer:
Subtract 9 from both sides of the equation, and then multiply both sides of the equation by –\(\frac{1}{2}\); v = -8.
If: -2v + 9 = 25
Then: -2v + 9-9 = 25-9 Subtraction property of equality for the additive inverse of 9
If: -2v + 0 = 16
Then: -2v = 16 Additive identity
If: -2v = 16
Then: –\(\frac{1}{2}\) (-2v) = –\(\frac{1}{2}\) (16) Multiplication property of equality using the multiplicative inverse of -2
If: 1 v = -8
Then: v = -8 Multiplicative identity
Question 3.
\(\frac{1}{3}\) y-18 = 2
Answer:
Add 18 to both sides of the equation, and then multiply both sides of the equation by 3; y = 60.
If: \(\frac{1}{3}\) y-18 = 2
Then: \(\frac{1}{3}\) y-18 + 18 = 2 + 18 Addition property of equality for the additive inverse of –18
If: \(\frac{1}{3}\) y + 0 = 20
Then: \(\frac{1}{3}\) y = 20 Additive identity
If: \(\frac{1}{3}\) y = 20
Then: 3(\(\frac{1}{3}\) y) = 3 (20) Multiplication property of equality using the multiplicative inverse of \(\frac{1}{3}\)
If: 1 y = 60
Then: y = 60 Multiplicative identity
Question 4.
6-8p = 38
Answer:
Subtract 6 from both sides of the equation, and then multiply both sides of the equation by –\(\frac{1}{8}\); p = -4.
If: 6-8p = 38
Then: 6-6-8p = 38-6 Subtraction property of equality for the additive inverse of 6
If: 0 + (-8p) = 32
Then: -8p = 32 Additive identity
If: -8p = 32
Then: (-\(\frac{1}{8}\))(-8p) = (-\(\frac{1}{8}\))32 Multiplication property of equality using the multiplicative inverse of -8
If: 1 p = -4
Then: p = -4 Multiplicative identity
Question 5.
15 = 5k-13
Answer:
Add 13 to both sides of the equation, and then multiply both sides of the equation by \(\frac{1}{5}\); k = 5.6.
If: 15 = 5k-13
Then: 15 + 13 = 5k-13 + 13 Addition property of equality for the additive inverse of -13
If: 28 = 5k + 0
Then: 28 = 5k Additive identity
If: 28 = 5k
Then: (\(\frac{1}{5}\))28 = (\(\frac{1}{5}\))5k Multiplication property of equality using the multiplicative inverse of 5
If: 5.6 = 1k
Then: 5.6 = k Multiplicative identity
Eureka Math Grade 7 Module 2 Lesson 22 Exit Ticket Answer Key
Susan and Bonnie are shopping for school clothes. Susan has $50 and a coupon for a $10 discount at a clothing store where each shirt costs $12.
Susan thinks that she can buy three shirts, but Bonnie says that Susan can buy five shirts. The equations they used to model the problem are listed below. Solve each equation algebraically, justify your steps, and determine who is correct and why?

Answer:
Bonnie is correct. The equation that would model this situation is 12n-10 = 50. Solving this equation would involve making zero by adding 10. And by doing so, 12n-10 + 10 = 50 + 10, we arrive at 12n = 60. So, if a group of shirts that cost $12 each totals $60, then there must be five shirts since \(\frac{60}{12}\) equals 5.
Bonnie’s Equation:
12n-10 = 50
12n-10 + 10 = 50 + 10 Addition property of equality for the additive inverse of -10
12n + 0 = 60
12n = 60 Additive identity
(\(\frac{1}{12}\))12n = (\(\frac{1}{12}\))60 Multiplication property of equality using the multiplicative inverse of 12
1n = 5
n = 5 Multiplicative identity
Susan’s Equation:
12n + 10 = 50
12n + 10-10 = 50-10 Subtraction property of equality for the additive inverse of 10
12n + 0 = 40
12n = 40 Additive identity
(\(\frac{1}{12}\))12n = (\(\frac{1}{12}\))40 Multiplication property of equality using the multiplicative inverse of 12
1n = 3 \(\frac{1}{3}\)
n = 3 \(\frac{1}{3}\) Multiplicative identity