Engage NY Eureka Math 7th Grade Module 2 Lesson 15 Answer Key
Eureka Math Grade 7 Module 2 Lesson 15 Exercise Answer Key
Exercise 1.
a. In the space below, create a word problem that involves integer multiplication. Write an equation to model the situation.
Answer:
Answers will vary.
Both times we went to the fair, I borrowed $3 from my older brother. -$3 × 2 = -$6
b. Now change the word problem by replacing the integers with non-integer rational numbers (fractions or decimals), and write the new equation.
Answer:
Answers will vary.
Both times we went to the fair, I borrowed $3.50 from my older brother. -$3.50×2=-$7.00
c. Was the process used to solve the second problem different from the process used to solve the first? Explain.
Answer:
No, the process was the same. Both times I had a positive number multiplied by a negative number, so the product is a negative number. The process, multiplication, is represented as repeated addition:
-$3.50+(-$3.50)= -$7.00.
→ Was the process for solving the second problem different from the process you used to solve the problem when it contained only integers?
→ No
Students record the rules in Exercise 1, part (d) of their student materials.
d. The Rules for Multiplying Rational Numbers are the same as the Rules for Multiplying Integers:
Answer:
1. Multiply the absolute values of the two rational numbers.
2. If the two numbers (factors) have the same sign, their product is positive.
3. If the two numbers (factors) have opposite signs, their product is negative.
Exercise 2.
a. In one year, Melinda’s parents spend $2,640.90 on cable and internet service. If they spend the same amount each month, what is the resulting monthly change in the family’s income?
Answer:
-2,640.90 ÷ 12 = -220.08
The average monthly change to their income is about -$220.08.
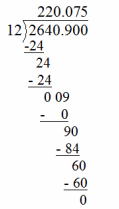
→ Are the rules for dividing rational numbers the same as the rules for dividing integers?
→ Yes
Students record the rules in Exercise 2, part (b) of their student materials.
b. The Rules for Dividing Rational Numbers are the same as the Rules for Dividing Integers:
1. Divide the absolute values of the two rational numbers.
2. If the two numbers (dividend and divisor) have the same sign, their quotient is positive.
3. If the two numbers (dividend and divisor) have opposite signs, their quotient is negative.
Exercise 3.
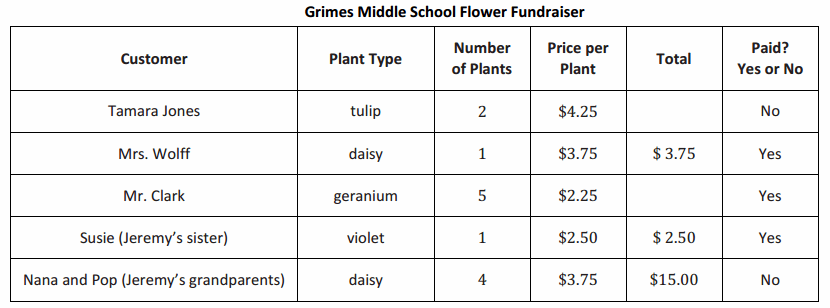
Use the fundraiser chart to help answer the questions that follow.
Answer:
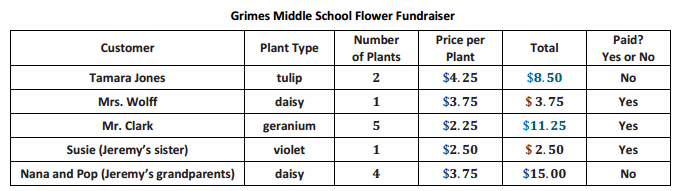
Jeremy is selling plants for the school’s fundraiser, and listed above is a chart from his fundraiser order form. Use the information in the chart to answer the following questions. Show your work, and represent the answer as a rational number; then, explain your answer in the context of the situation.
a. If Tamara Jones writes a check to pay for the plants, what is the resulting change in her checking account balance?
Answer:
-4.25 × 2 = -8.50
Numerical Answer:
Answer:
-8.50
Explanation:
Answer:
Tamara Jones will need to deduct $8.50 from her checking account balance.
b. Mr. Clark wants to pay for his order with a $20 bill, but Jeremy does not have change. Jeremy tells Mr. Clark he will give him the change later. How will this affect the total amount of money Jeremy collects? Explain. What rational number represents the change that must be made to the money Jeremy collects?
Answer:
2.25 × 5 = 11.25 20.00 – 11.25 = 8.75
Numerical Answer:
Answer:
-8.75
Explanation:
Answer:
Jeremy collects too much money. He owes Mr. Clark $8.75. The adjustment Jeremy needs to make is -$8.75.
c. Jeremy’s sister, Susie, borrowed the money from their mom to pay for her order. Their mother has agreed to deduct an equal amount of money from Susie’s allowance each week for the next five weeks to repay the loan. What is the weekly change in Susie’s allowance?
Answer:
-2.50 ÷ 5 = – 0.50
Numerical Answer:
Answer:
-0.50
Explanation:
Answer:
Susie will lose $0.50 of her allowance each week.
d. Jeremy’s grandparents want to change their order. They want to order three daisies and one geranium, instead of four daisies. How does this change affect the amount of their order? Explain how you arrived at your answer.
Answer:
Original Order: 3.75 × 4 = 15.00
New Order: 3.75 × 3 + 2.25 = 11.25 + 2.25 = 13.50
15.00-13.50=1.50
Numerical Answer: 1.50
Explanation: Jeremy’s grandparents will get back $1.50 since the change in their order made it cheaper.
I got my answer by first calculating the cost of the original order. Second, I calculated the cost of the new order. Finally, I subtracted the two order totals to determine the difference in cost.
e. Jeremy approaches three people who do not want to buy any plants; however, they wish to donate some money for the fundraiser when Jeremy delivers the plants one week later. If the people promise to donate a total of $14.40, what will be the average cash donation?
Answer:
14.40 ÷ 3 = 4.80
Numerical Answer: 4.80
Explanation: The average cash donation will be $4.80 per person.
f. Jeremy spends one week collecting orders. If 22 people purchase plants totaling $270, what is the average amount of Jeremy’s sale?
Answer:
270 ÷ 22 ≈ 12.272
Numerical Answer: 12.27
Explanation: The average sale is about $12.27.
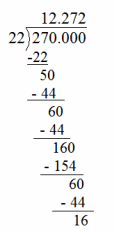
Eureka Math Grade 7 Module 2 Lesson 15 Problem Set Answer Key
Question 1.
At lunch time, Benjamin often borrows money from his friends to buy snacks in the school cafeteria. Benjamin borrowed $0.75 from his friend Clyde five days last week to buy ice cream bars. Represent the amount Benjamin borrowed as the product of two rational numbers; then, determine how much Benjamin owed his friend last week.
Answer:
5 (-0.75)=-3.75
Benjamin owed Clyde $3.75.
Question 2.
Monica regularly records her favorite television show. Each episode of the show requires 3.5% of the total capacity of her video recorder. Her recorder currently has 62% of its total memory free. If Monica records all five episodes this week, how much space will be left on her video recorder?
Answer:
62 + 5(-3.5) = 62 + (-17.5) = 44.5
Monica’s recorder will have 44.5% of its total memory free.
For Problems 3–5, find at least two possible sets of values that will work for each problem.
Question 3.
Fill in the blanks with two rational numbers (other than 1 and -1). ____ × (-\(\frac{1}{2}\)) × ____ = -20
What must be true about the relationship between the two numbers you chose?
Answer:
Answers may vary. Two possible solutions are 10 and 4 or -10 and -4. The two numbers must be factors of 40, and they must both have the same sign.
Question 4.
Fill in the blanks with two rational numbers (other than 1 and -1). -5.6 × 100÷ 80 × ____ × ____ =700
What must be true about the relationship between the two numbers you chose?
Answer:
Answers may vary. Two possible solutions are -50 and 2 or 25 and -4. The two numbers must be factors of -100, and they must have opposite signs.
Question 5.
Fill in the blanks with two rational numbers. ____ × ____ = -0.75
What must be true about the relationship between the two numbers you chose?
Answer:
Answers may vary. Two possible solutions are -3 and 0.25 or 0.5 and -1.5. The two numbers must be factors of -0.75, and they must have opposite signs.
For Problems 6–8, create word problems that can be represented by each expression, and then represent each product or quotient as a single rational number.
Question 6.
8×(-0.25)
Answer:
Answers may vary.
Example: Stacey borrowed a quarter from her mother every time she went to the grocery store so that she could buy a gumball from the gumball machine. Over the summer, Stacey went to the grocery store with her mom eight times. What rational number represents the dollar amount change in her mother’s money due to the purchase of gumballs?
Answer: -2
Question 7.
-6÷(1\(\frac{1}{3}\))
Answer:
Answers may vary.
Example: There was a loss of $6 on my investment over one-and-a-third months. Based on this, what was the investment’s average dollar amount change per month?
Answer: -4.50
Question 8.
–\(\frac{1}{2}\) × 12
Answer:
Answers may vary.
Example: I discarded exactly half of my card-point total in the Integer Game. If my card-point total was 12 before I discarded, which rational number represents the change to my hand’s total card-point total?
Answer: -6
Eureka Math Grade 7 Module 2 Lesson 15 Exit Ticket Answer Key
Harrison made up a game for his math project. It is similar to the Integer Game; however, in addition to integers, there are cards that contain other rational numbers such as -0.5 and -0.25. Write a multiplication or division equation to represent each problem below. Show all related work.
Question 1.
Harrison discards three -0.25 cards from his hand. How does this affect the overall point value of his hand? Write an equation to model this situation.
Answer:
-3 (-0.25) = 0.75
The point value of Harrison’s hand will increase by 0.75 points.
Question 2.
Ezra and Benji are playing the game with Harrison. After Ezra doubles his hand’s value, he has a total of -14.5 points. What was his hand’s value before he doubled it?
Answer:
-14.5 ÷ 2 = -7.25
Before Ezra doubled his hand, his hand had a point value of -7.25.
Question 3.
Benji has four -0.5 cards. What is his total score?
Answer:
4 × (-0.5) = -2.0
Benji’s total score is -2.0 points.
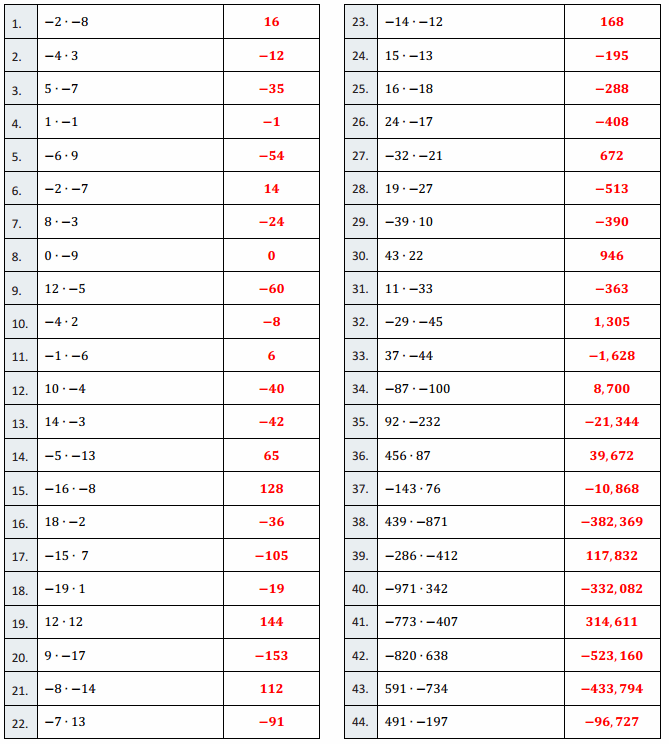
Eureka Math Grade 7 Module 2 Lesson 15 Integer Multiplication Round 1 Answer Key
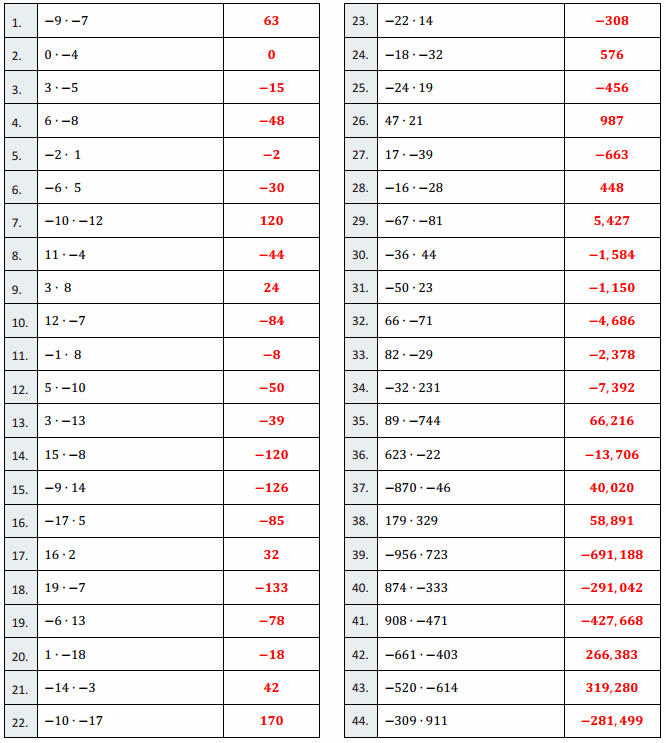
Directions: Determine the product of the integers, and write it in the column to the right.
Answer:
Eureka Math Grade 7 Module 2 Lesson 15 Integer Multiplication Round 2 Answer Key
Answer: