Engage NY Eureka Math 7th Grade Module 2 Lesson 13 Answer Key
Eureka Math Grade 7 Module 2 Lesson 13 Example Answer Key
Example 1.
Representations of Rational Numbers in the Real World
Following the Opening Exercise and class discussion, describe why we need to know how to represent rational numbers in different ways.
Answer:
Different situations in the real world require different representations of rational numbers. Because of common usage in life outside of the classroom, we may automatically know that a quarter of a dollar is the same as 25 cents, or a quarter, but for people who are used to measuring money in only decimals, a quarter of a dollar might not make much sense.
Example 2.
Using Place Values to Write (Terminating) Decimals as Equivalent Fractions
a. What is the value of the number 2.25? How can this number be written as a fraction or mixed number?
Answer:
Two and twenty-five hundredths or 2\(\frac{25}{100}\)
→ How do we rewrite this fraction (or any fraction) in its simplest form?
→ If a factor is common to both the numerator and denominator of a fraction, the fraction can be simplified, resulting in a fraction whose numerator and denominator only have a common factor of 1 (the numerator and denominator are relatively prime).
b. Rewrite the fraction in its simplest form showing all steps that you use.
Answer:
Answer:
\(\frac{25}{100}\) = \(\frac{25}{4×25}\) = \(\frac{1}{4}\) → 2\(\frac{25}{100}\) = 2\(\frac{1}{4}\)
c. What is the value of the number 2.025? How can this number be written as a mixed number?
Answer:
Two and twenty-five thousandths, or 2\(\frac{25}{1,000}\)
d. Rewrite the fraction in its simplest form showing all steps that you use.
Answer:
\(\frac{25}{1,000}\) = \(\frac{25}{(100×10)}\)
\(\frac{25}{4×25×10}\) = \(\frac{1}{40}\) → 2\(\frac{25}{1,000}\) = 2\(\frac{1}{40}\)
Example 3.
Converting Fractions to Decimals—Fractions with Denominators Having Factors of only 2 or 5
a. What are decimals?
Answer:
Decimals specify points on the number line by repeatedly subdividing intervals into tenths. If a unit is divided into ten equal-sized pieces, one piece would be one-tenth of that unit.
b. Use the meaning of decimal to relate decimal place values.
Answer:
Each place value in a decimal is \(\frac{1}{10}\) of the value of the place to its left. This means that the denominators of the fractions that represent each decimal place value must be powers of ten.
c. Write the number \(\frac{3}{100}\) as a decimal. Describe your process.
Answer:
The decimal form is 0.03. The fraction includes a power of ten, 100, as its denominator. The value of the second decimal place is \(\frac{1}{100}\), so \(\frac{3}{100}\) in decimal form is 0.03.
→ How could we obtain an equivalent fraction to \(\frac{3}{20}\) with a power of ten in the denominator?
→ If there was another factor of 5 in the denominator, then we would have an equal number of 2’s and 5’s resulting in a power of ten. If we multiply the fraction by \(\frac{5}{5}\) (or 1), we get an equivalent fraction with a power of ten in its denominator.
d. Write the number \(\frac{3}{20}\) as a decimal. Describe your process.
Answer:
The fractional form is \(\frac{3}{20}\) = \(\frac{3}{2^{2} \times 5}\). The denominator lacks a factor of 5 to be a power of ten. To arrive at the decimal form, I multiply the fractional form by \(\frac{5}{5}\) to arrive at \(\frac{3}{2^{2} \times 5}\) × \(\frac{5}{5}\) = \(\frac{3 \times 5}{2^{2} \times 5^{2}}\) = \(\frac{15}{100}\), and \(\frac{15}{100}\) = 0.15.
e. Write the number \(\frac{10}{25}\) as a decimal. Describe your process.
Answer:
The fractional form is \(\frac{10}{25}\) = \(\frac{2×5}{5×5}\) ; and, since \(\frac{5}{5}\) = 1, then \(\frac{2×5}{5×5}\) = \(\frac{2}{5}\). The denominator lacks a factor of 2 to be a power of ten. To arrive at the decimal form, I multiply the fractional form by \(\frac{2}{2}\) to arrive at \(\frac{2}{5}\) × \(\frac{2}{2}\) = \(\frac{4}{10}\), and \(\frac{4}{10}\) = 0.4.
f. Write the number \(\frac{8}{40}\) as a decimal. Describe your process.
Answer:
The fractional form is \(\frac{8}{40}\) = \(\frac{2^{3}}{2^{3} \times 5}\). There are factors of 2 in the numerator and denominator that will cancel. If I leave one factor of two in the denominator, it will be 10 (a power of ten).
\(\frac{2^{3}}{2^{3} \times 5}\) = \(\frac{2^{2} \times 2}{2^{2} \times 2 \times 5}\) = \(\frac{2}{2 \times 5}\) = \(\frac{2}{10}\) = 0.2
Eureka Math Grade 7 Module 2 Lesson 13 Exercise Answer Key
Exercise 1.
Use place value to convert each terminating decimal to a fraction. Then rewrite each fraction in its simplest form.
a. 0.218
Answer:
\(\frac{218}{1,000}\) = \(\frac{109×2}{500×2}\) = \(\frac{109}{100}\) → 0.218 = \(\frac{109}{500}\)
b. 0.16
Answer:
\(\frac{16}{100}\) = \(\frac{4×4}{4×25}\) = \(\frac{4}{25}\) → 0.16 = \(\frac{4}{25}\)
c. 2.72
Answer:
\(\frac{72}{100}\) = \(\frac{4×18}{4×25}\) = \(\frac{18}{25}\) → 2.72 = 2\(\frac{18}{25}\)
d. 0.0005
Answer:
\(\frac{5}{10,000}\) = \(\frac{5×1}{5×2,000}\) = \(\frac{1}{2,000}\) → 0.0005 = \(\frac{1}{2,000}\)
→ What do you notice about the denominators of fractions that represent each decimal place?
→ The denominators are all powers of 10.
→ What are the prime factors of 10? 100? 1,000?
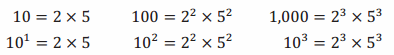
→ What prime factors make up the powers of 10?
→ The powers of 10 contain only the factors 2 and 5, and, in each case, the number of factors of 2 and 5 are equal to the number of factors of 10.
→ How can the prime factorization of the powers of ten be used to write fractions in decimal form?
→ Find an equivalent fraction whose denominator is a power of ten, then write the decimal representation using place values.
Exercise 2.
Convert each fraction to a decimal using an equivalent fraction.
a. \(\frac{3}{16}\) =
Answer:
\(\frac{3}{16}\) = \(\frac{3}{2×4}\) → \(\frac{3 \times 5^{4}}{2^{4} \times 5^{4}}\) = \(\frac{1,875}{10,000}\) → \(\frac{1875}{10,000}\) = 0.1875
b. \(\frac{7}{5}\)=
\(\frac{7}{5}\) → \(\frac{7×2}{5×2}\) = \(\frac{14}{10}\) → \(\frac{14}{10}\) = 1 \(\frac{4}{10}\) = 1.4
c. \(\frac{11}{32}\)=
\(\frac{11}{32}\) = \(\frac{11}{2^{5}}\) → \(\frac{11 \times 5^{5}}{2^{5} \times 5^{5}}\) = \(\frac{34,375}{100,000}\) → \(\frac{34375}{100,000}\) = 0.34375
d. \(\frac{35}{50}\)=
\(\frac{35}{50}\) = \(\frac{5 \times 7}{5^{2} \times 2}\) → \(\frac{7}{5×2}\) = \(\frac{7}{10}\) → \(\frac{7}{10}\) = 0.7
Eureka Math Grade 7 Module 2 Lesson 13 Problem Set Answer Key
Question 1.
Convert each terminating decimal to a fraction in its simplest form.
a. 0.4
Answer:
0.4 = \(\frac{2}{5}\)
b. 0.16
Answer:
0.16 = \(\frac{4}{25}\)
c. 0.625
Answer:
0.625 = \(\frac{5}{8}\)
d. 0.08
Answer:
0.08 = \(\frac{2}{25}\)
e. 0.012
Answer:
0.012 = \(\frac{3}{250}\)
Question 2.
Convert each fraction or mixed number to a decimal using an equivalent fraction.
a. \(\frac{4}{5}\)
Answer:
\(\frac{4}{5}\) = 0.8
b. \(\frac{3}{40}\)
Answer:
\(\frac{3}{40}\) = 0.075
c. \(\frac{8}{200}\)
Answer:
\(\frac{8}{200}\) = 0.04
d. 3\(\frac{5}{16}\)
Answer:
3 \(\frac{5}{16}\) = 3.3125
Question 3.
Tanja is converting a fraction into a decimal by finding an equivalent fraction that has a power of 10 in the denominator. Sara looks at the last step in Tanja’s work (shown below) and says that she cannot go any further. Is Sara correct? If she is, explain why. If Sara is incorrect, complete the remaining steps.
\(\frac{72}{480}\) = \(\frac{2^{3} \cdot 3^{2}}{2^{5} \cdot 3 \cdot 5}\)
Answer:
Tanja can finish the conversion since there is a factor pair of 3’s in the numerator and denominator that can be divided out with a quotient of 1.
Remaining Steps:
\(\frac{72}{480}\) = \(\frac{2^{3} \cdot 3^{2}}{2^{5} \cdot 3 \cdot 5}\) = \(\frac{3}{2^{2} \cdot 5}\)(\(\frac{5}{5}\)) = \(\frac{3 \cdot 5}{2^{2} \cdot 5^{2}}\) = \(\frac{15}{100}\)
Answer:0.5
Eureka Math Grade 7 Module 2 Lesson 13 Exit Ticket Answer Key
Question 1.
Write 3.0035 as a fraction. Explain your process.
Answer:
The right-most decimal place is the ten-thousandths place, so the number in fractional form would be 3\(\frac{35}{10,000}\). There are common factors of 5 in the numerator and denominator, and dividing both by these results in the fraction 3\(\frac{7}{2,000}\).
Question 2.
This week is just one of 40 weeks that you spend in the classroom this school year. Convert the fraction \(\frac{1}{40}\) to decimal form.
Answer:
\(\frac{1}{40}\) = \(\frac{1}{2^{3} \times 5}\)×\(\frac{5^{2}}{5^{2}}\) = \(\frac{5^{2}}{2^{3} \times 5^{3}}\) = \(\frac{25}{1,000}\) = 0.025