Engage NY Eureka Math Grade 6 Module 6 Lesson 4 Answer Key
Eureka Math Grade 6 Module 6 Lesson 4 Example Answer Key
Example 1 (5 minutes): Frequency Table with Intervals
The boys’ and girls’ basketball teams at Roosevelt Middle School wanted to raise money to help buy new uniforms. They decided to sell baseball caps with the school logo on the front to family members and other interested fans. To obtain the correct cap size, students had to measure the head circumference (distance around the head) of the adults who wanted to order a cap. The following data set represents the head circumferences, in millimeters (mm), of the adults.
513, 525, 531, 533, 535, 535, 542, 543, 546, 549, 551, 552, 552, 553, 554, 555, 560, 561, 563, 563, 563, 565, 565, 568, 568, 571, 571, 574, 577, 580, 583, 583, 584, 585, 591, 595, 598, 603, 612, 618
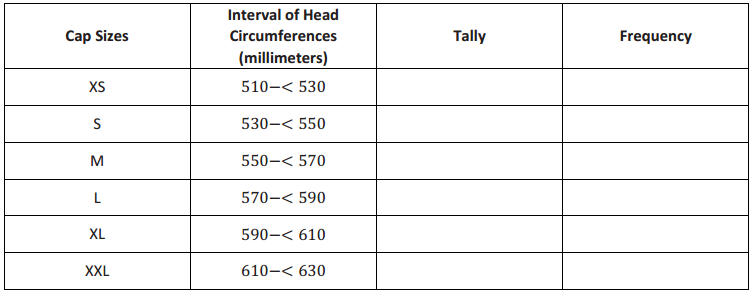
The caps come in six sizes: XS, S, M, L, XL, and XXL. Each cap size covers an interval of head circumferences. The cap manufacturer gave students the table below that shows the interval of head circumferences for each cap size. The
interval 510 -< 530 represents head circumferences from 510 mm to 530 mm, not including 530.
Exercises 1 – 4:
Exercise 1.
What size cap would someone with a head circumference of 570 mm need?
Answer:
Someone with a head circumference of 570 mm would need o large.
Exercise 2.
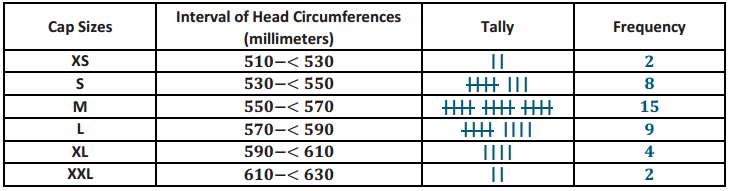
Complete the tally and frequency columns in the table in Example 1 to determine the number of each size cap students need to order for the adults who wanted to order a cap.
Answer:
Exercise 3.
What head circumference would you use to describe the center of the data?
Answer:
The head circumferences center somewhere around 550 mm to 570 mm. This corresponds to a cap size of medium. (Answers may vary, but student responses should be around the center of the data distribution.)
Exercise 4.
Describe any patterns that you observe in the frequency column.
Answer:
The numbers start small but increase to 15 and then go back down.
Example 2: Histogram
One student looked at the tally column and said that it looked somewhat like a bar graph turned on its side. A histogram is a graph that is like a bar graph except that the horizontal axis is a number line that is marked off in equal intervals.
To make a histogram:
1. Draw a horizontal line, and mark the intervals.
2. Draw a vertical line, and label it Frequency.
3. Mark the Frequency axis with a scale that starts at 0 and goes up to something that is greater than the largest frequency in the frequency table.
4. For each interval, draw a bar over that interval that has a height equal to the frequency for that interval.
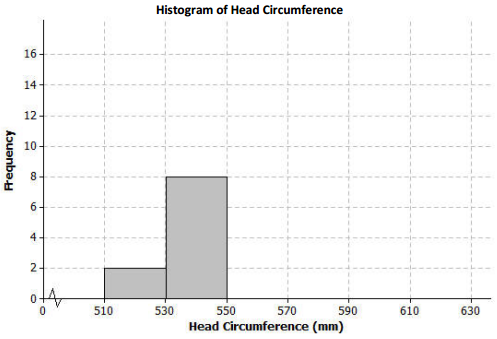
The first two bars of the histogram have been drawn below.
Exercises 5 – 9:
Exercise 5.
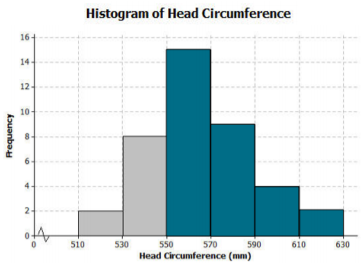
Complete the histogram by drawing bars whose heights are the frequencies for the other intervals.
Answer:
Exercise 6.
Based on the histogram, describe the center of the head circumferences.
Answer:
The center of the head circumferences is around 560 mm. (Answers may vary, but student responses should be around the center of the data distribution.)
Exercise 7.
How would the histogram change if you added head circumferences of 551 mm and 569 mm to the data set?
Answer:
The bar for the 550 to 570 mm interval would go up to 17.
Exercise 8.
Because the 40 head circumference values were given, you could have constructed a dot plot to display the head circumference data. What information is lost when a histogram is used to represent a data distribution instead of a dot plot?
Answer:
In a dot plot, you can see individual values. In a histogram, you only see the total number of values in an interval.
Exercise 9.
Suppose that there had been 200 head circumference measurements in the data set. Explain why you might prefer to summarize this data set using a histogram rather than a dot plot.
Answer:
There would be too many dots on a dot plot, and it would be hard to read. A histogram would work fora large data set because the frequency scale can be adjusted.
Example 3: Shape of the Histogram
A histogram is useful to describe the shape of the data distribution. It is important to think about the shape of a data distribution because depending on the shape, there are different ways to describe important features of the distribution, such as center and variability.
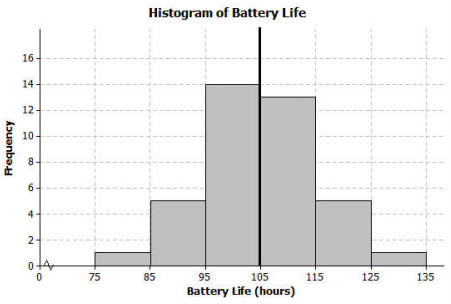
A group of students wanted to find out how long a certain brand of AA batteries lasted. The histogram below shows the data distribution for how long (in hours) that some AA batteries lasted. Looking at the shape of the histogram, notice how the data mound up around a center of approximately 105 hours. We would describe this shape as mound shaped or symmetric. If we were to draw a line down the center, notice how each side of the histogram is approximately the same, or a mirror image of the other. This means the histogram is approximately symmetrical.
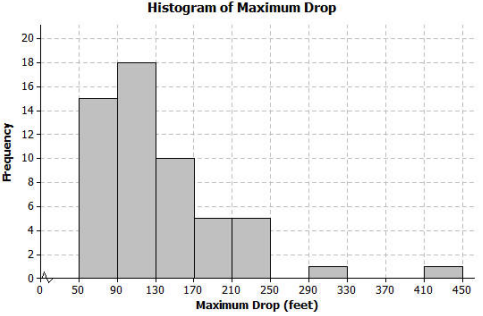
Another group of students wanted to investigate the maximum drop length for roller coasters. The histogram below shows the maximum drop (in feet) of a selected group of roller coasters. This histogram has a skewed shape. Most of the data are in the intervals from 50 feet to 170 feet. But there is one value that falls in the interval from 290 feet to 330 feet and one value that falls in the interval from 410 feet to 550 feet. These two values are unusual (or not typical) when compared to the rest of the data because they are much greater than most of the data.
Exercises 10 – 12:
Exercise 10.
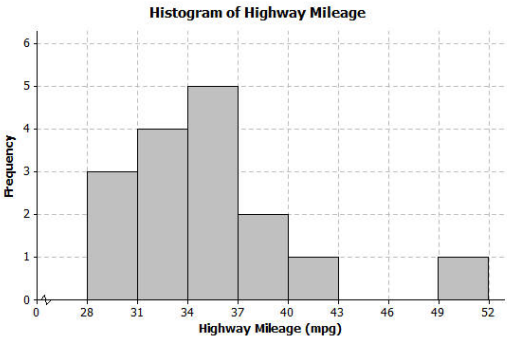
The histogram below shows the highway miles per gallon of different compact cars.
Answer:
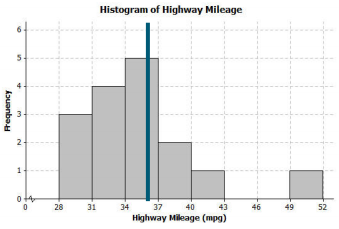
a. Describe the shape of the histogram as approximately symmetric, skewed left, or skewed right.
Answer:
Skewed right toward the larger values.
b. Draw a vertical line on the histogram to show where the typical number of miles per gallon for a compact car would be.
Answer:
The vertical line to show the typical number of miles per gallon would be around 36.
c. What does the shape of the histogram tell you about miles per gallon for compact cars?
Answer:
Most cars get around 31 to 40 mpg. But there was one car that got between 49 and 52 mpg.
Exercise 11.
Describe the shape of the head circumference histogram that you completed in Exercise 5 as approximately symmetric, skewed left, or skewed right.
Answer:
The shape of the histogram is approximately symmetric.
Exercise 12.
Another student decided to organize the head circumference data by changing the width of each interval to be 10 instead of 20. Below is the histogram that the student made.
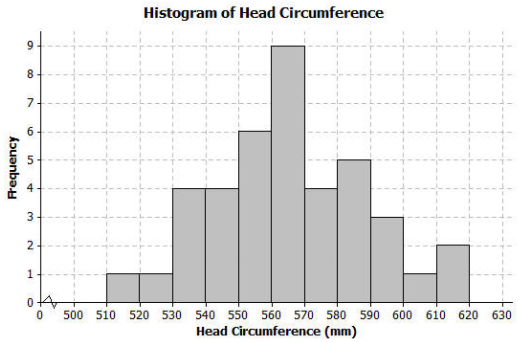
a. How does this histogram compare with the histogram of the head circumferences that you completed in Exercise 5?
Answer:
Answers will vary; both histograms have the same general shape and center.
b. Describe the shape of this new histogram as approximately symmetric, skewed left, or skewed right.
Answer:
The shape of this new histogram is approximately symmetric.
c. How many head circumferences are in the interval from 570 to 590 mm?
Answer:
There are 9 head circumferences in the interval from 570 to 590 mm.
d. In what interval would a head circumference of 571 mm be included? In what interval would a head circumference of 610 mm be included?
Answer:
The head circumference of 571 mm is in the interval from 570 to 580 mm. The head circumference of 610 mm is in the interval from 610 to 620 mm.
Eureka Math Grade 6 Module 6 Lesson 4 Problem Set Answer Key
Question 1.
The following histogram summarizes the ages of the actresses whose performances have won in the Best Leading Actress category at the annual Academy Awards (i.e., Oscars).
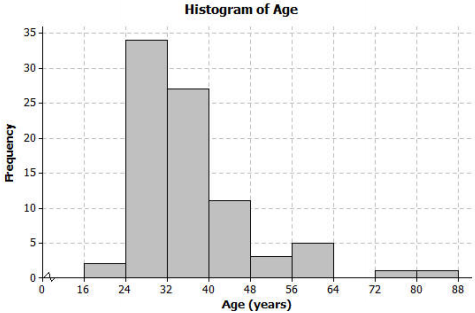
a. Which age interval contains the most actresses? How many actresses are represented in that interval?
Answer:
The interval 24 to 32 contains the most actresses. There are 34 actresses whose age falls into that category.
b. Describe the shape of the histogram.
Answer:
The shape of the histogram is skewed to the right.
c. What does the histogram tell you about the ages of actresses who won the Oscar for best actress?
Answer:
Most of the ages are between 24 and 40, with two ages much larger than the rest.
d. Which interval describes the center of the ages of the actresses?
Answer:
The interval of 32 to 40 describes the center of the ages. (Answers may vary, but student responses should be around the center of the data distribution.)
e. An age of 72 would be included in which interval?
Answer:
The age of 72 Is in the interval from 72 to 80.
Question 2.
The frequency table below shows the seating capacity of arenas for NBA basketball teams.
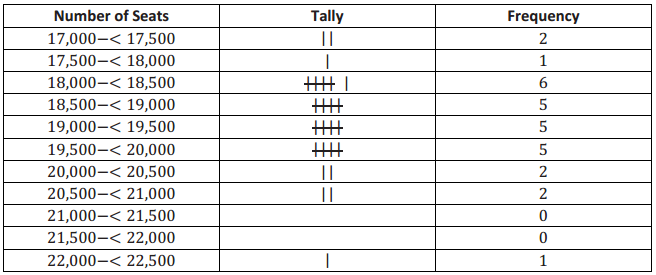
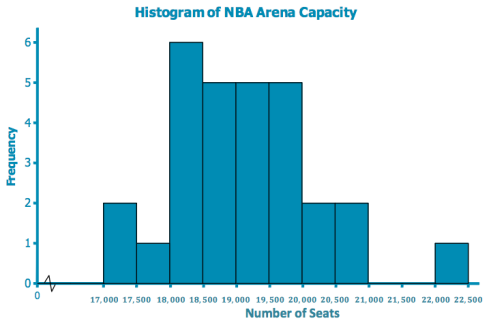
a. Draw a histogram for the number of seats in the NBA arenas data. Use the histograms you have seen throughout this lesson to help you in the construction of your histogram.
Answer:
b. What is the width of each interval? How do you know?
Answer:
The width of each interval is 500.
Subtract the values identifying on interval.
c. Describe the shape of the histogram.
Answer:
The shape of the histogram is skewed to the right.
d. Which interval describes the center of the number of seats data?
Answer:
The interval of 19,000 to 19, 500 describes the center. (Answers may vary, but student responses should be around the center of the dota distribution.)
Question 3.
Listed are the grams of carbohydrates in hamburgers at selected fast food restaurants.
33 40 66 45 28 30 52 40 26 42
42 44 33 44 45 32 45 45 52 24
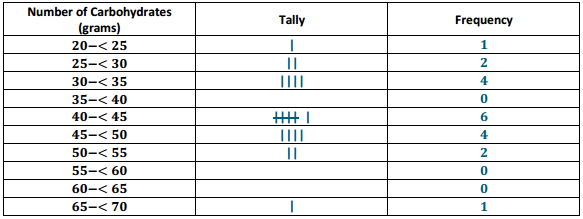
a. Complete the frequency table using the given intervals of width 5.
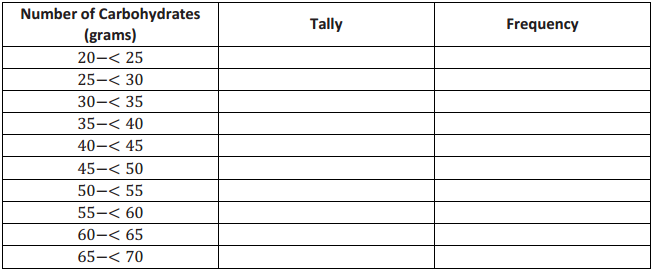
Answer:
b. Draw a histogram of the carbohydrate data.
Answer:
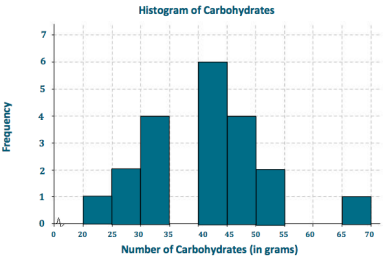
c. Describe the center and shape of the histogram.
Answer:
The center is around 40; the histogram is mound shaped and approximately symmetric. (Answers may vary, but student responses for describing the center should be around the center of the data distribution.)
d. In the frequency table below, the intervals are changed. Using the carbohydrate data above, complete the
frequency table with intervals of width 10.
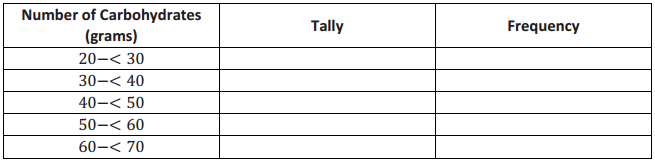
Answer:
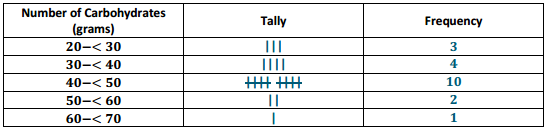
e. Draw a histogram.
Answer:
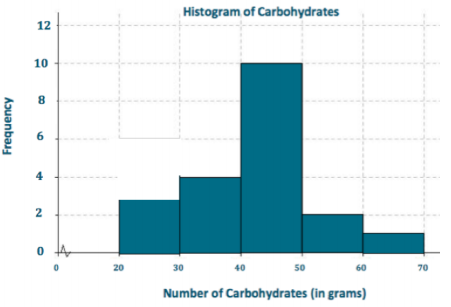
Question 4.
Use the histograms that you constructed in Exercise 3 parts (b) and (e) to answer the following questlons.
a. Why are there fewer bars in the histogram in part (e) than the histogram in part (b)?
Answer:
There are fewer bars in part (e) because the width of the interval changed from 5 grams to 10 grams, so there ore fewer intervals.
b. Did the shape of the histogram in pait (e) change from the shape of the histogram in part (b)?
Answer:
Generally, both are approximately symmetric and mound shaped, but the histogram in part (b) has gaps.
c. Did your estimate of the center change from the histogram in part (b) to the histogram in part (e)?
Answer:
The centers of the two histograms ore about the same.
Eureka Math Grade 6 Module 6 Lesson 4 Exit Ticket Answer Key
The frequency table below shows the length of selected movies shown in a local theater over the past six months.
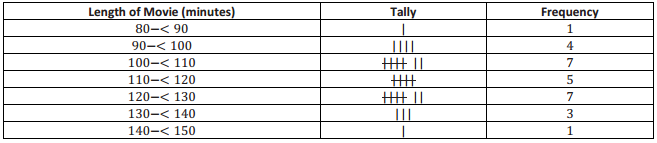
Question 1.
Construct a histogram for the length of movies data.
Answer:
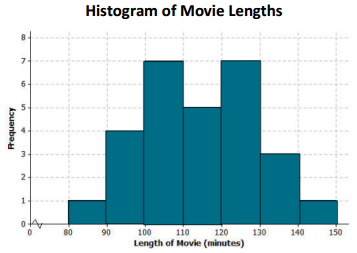
Question 2.
Describe the shape of the histogram.
Answer:
The shape of the histogram is mound-shaped and approximately symmetric.
Question 3.
What does the histogram tell you about the length of movies?
Answer:
Most movie lengths were between 100 and 130 minutes.