Engage NY Eureka Math Grade 6 Module 6 Lesson 18 Answer Key
Eureka Math Grade 6 Module 6 Lesson 18 Example Answer Key
Example 1: Summary Information from Graphs
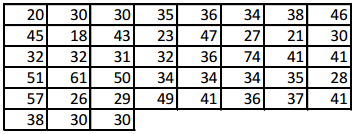
Here is a data set of the ages (in years) of 43 participants who ran in a 5-kilometer race.
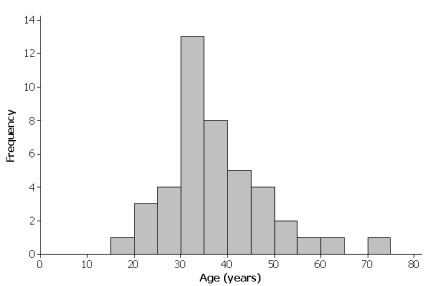
Here are some summary statistics, a dot plot, and a histogram for the data:
Minimum = 18, Q1 = 30, Median = 35, Q3 = 41, Maximum = 74; Mean = 36.8, MAD = 8.1

Eureka Math Grade 6 Module 6 Lesson 18 Exercise Answer Key
Exercises 1 – 7:
Exercise 1.
Based on the histogram, would you describe the shape of the data distribution as approximately symmetric or as skewed? Would you have reached this same conclusion looking at the dot plot?
Answer:
Both graphs show a slightly skewed right data distribution.
Exercise 2.
If there had been 500 participants instead of just 43, would you use a dot plot or a histogram to display the data?
Answer:
Dot plots do not work as well for large data sets, so with 500 ages, I would probably use a histogram to display the data distribution.
Exercise 3.
What is something you can see in the dot plot that is not as easy to seem the histogram?
Answer:
When using the histogram, we cannot determine the exact minimum or maximum age – for example, we only know that the minimum age is between 15 and 20 years of age. Also, we can only approximate the median (we cannot figure out the exact median value from a histogram).
Since the dot plot provides us with a dot for each observation, we can see the actual data values. With the dot plot, we can see that the minimum is 18. The median is the 22nd observation (since there are 43 observations), and the 22nd dot counting from left to right is 35 (we cannot be that precise with the histogram). We can also see that the oldest runner (74) appears to be a more extreme departure from the rest of the data in the dot plot.
Exercise 4.
Do the dot plot and the histogram seem to be centered in about the same place?
Answer:
Yes. As both graphs are based on the same data, they should generally communicate the same information regarding center.
Exercise 5.
Do both the dot plot and the histogram convey information about the variability in the age distribution?
Answer:
Yes, as both graphs are based on the same data, they should generally communicate the same information regarding variability. However, as mentioned earlier, the oldest runner (74) appears to be o more extreme departure from the rest of the data ¡rl the dot plot. This does not show up as much in the histogram.
Exercise 6.
If you did not have the original data set and only had the dot plot and the histogram, would you be able to find the value of the median age from the dot plot?
Answer:
Yes. See the response to Exercise 3.
Exercise 7.
Explain why you would only be able to estimate the value of the median if you only had a histogram of the data.
Answer:
The median is the 22nd ordered observation in this data set since there are 43 observations. Counting from left to right, we know that the first 21 observations are in the first 4 intervals: 15 – 20(1 value), 20 – 25(3 values), 25 – 30 (4 values), and 30 – 3 5 (13 values). Cumulatively, we have encountered the lowest observations by the time we are finished with the 30 – 35 interval. So, the 22nd value must be in the next interval, which is 35 – 40 years of age. We just cannot determine the exact value from the histogram.
Exercises 8 – 12: Graphs and Numerical Summaries
Exercise 8.
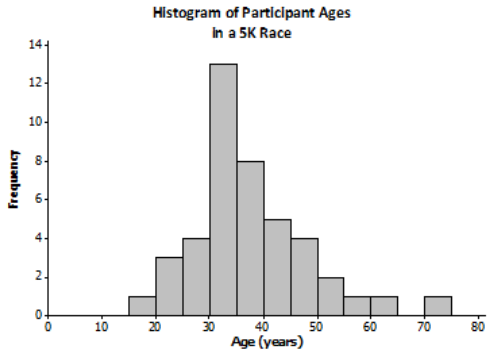
Suppose that a newspaper article was written about race. The article included the histogram shown here and also said, “The race attracted many older runners this year. The median age was 45.” Based on the histogram, how can you tell that this is an incorrect statement?
Answer:
Several answers are possible.
From the histogram, it appears that less than half of the runners are 45 or older (or alternatively, more than half of the runners are younger than 45). The value of the median is in the 35 – 40 age interval.
Exercise 9.
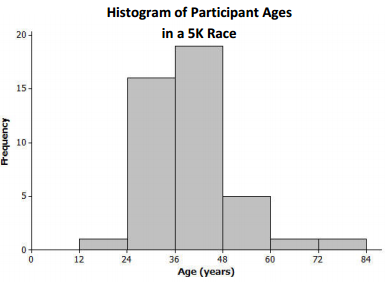
One of the histograms below is another correctly drawn histogram for the runners’ ages. Select the correct histogram, and explain how you determined which graph is correct (and which one is incorrect) based on the summary measures and dot plot.
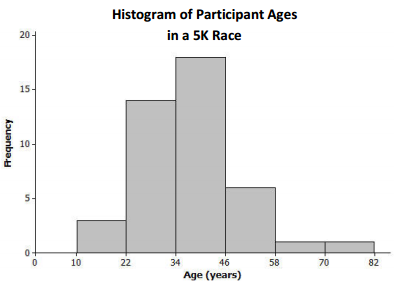
Answer:
One of the objectives of this question is to reinforce the idea that there is more than one way to draw a proper histogram for a distribution. This question is especially detail-oriented because students need to carefully reconcile components of the histogram with the data set given in Example 1.
The histogram on the right is the correct one because it is consistent with the dot pot/data. Most notably, the histogram on the right correctly shows there are 3 runners in the 10 – 22 age group, while the left histogram shows only 1 runner in the 12 – 2 4 age group (and there are actually 4 runners in that interval). Other intervals in the left histogram do not match the dot plot/data (e.g., the 48-60 group), so several answers are possible.
Exercise 10.
The histogram below represents the age distribution of the population of Kenya in 2010.
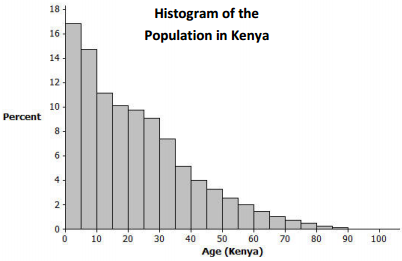
a. How do we know from the graph above that the first quartile (Q1) of this age distribution is between 5 and 10 years of age?
Answer:
Since a histogram should display information that is consistent with summary measures, we are seeking a data value such that 25% of the distribution is at or below that value. While the 0 – 5 age group represents approximately the lowest 17%. the next group (age 5 – 10) appears to account for approximately the next 15% of the distribution. This means that about 17% is below 5 and about 32% is below 10. So, the 25% mark would be somewhere between 5 and 10 years.
b. Someone believes that the median age in Kenya is about 30. Based on the histogram, is 30 years a good estimate of the median age for Kenya? Explain why it is or why it is not.
Answer:
The median does not appear to be 30 years of age. Specifically, the 50th percentile estimated by adding approximate percentages (and/or visually assessing the point at which the area seems split evenly) appears to be in the 15 – 20 age group.
Exercise 11.
The histogram below represents the age distribution of the population of the United States in 2010. Based on the histogram, which of the following ranges do you think includes the median age for the United States: 20 – 30, 30 – 40, or 40 – 50? Why?
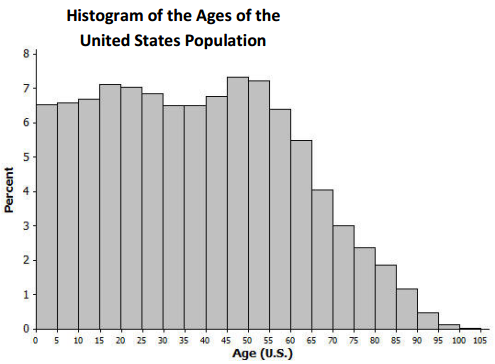
Answer:
Using similar arguments as described in the response to Exercise 10 part (b), the median appears to be in the 30 – 40 age group, most likely in the 35 – 40 interval.
Exercise 12.
Consider the following three-dot plots. Note: The same scale is used in each dot plot.
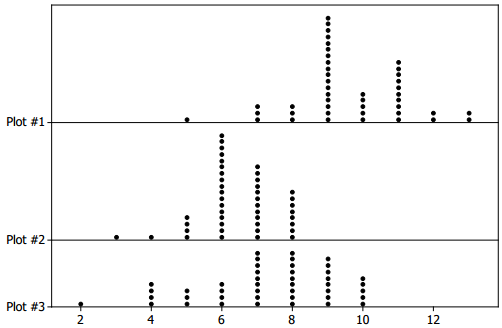
a. Which dot plot has a median of 8? Explain why you selected this dot plot over the other two.
Answer:
Plot 3 – It is the only distribution visually centered near 8, and one can tell that the 22 ordered observation (the median in this case) is 8.
b. Which dot plot has a mean of 9.6? Explain why you selected this dot plot over the other two.
Answer:
Plot 1 – This dot plot is the only dot plot for which there could be a mean value as high as 9.6. It is the only dot plot with values of 11, 12, and 13, and there are several of these values.
c. Which dot plot has a median of 6 and a range of S? Explain why you selected this dot plot over the other two.
Answer:
Plot 2 – It is the only dot plot that appears to be centered at 6. It is also the only dot plot with o range of 5 (each of the other dot plots has a range of 8).
Eureka Math Grade 6 Module 6 Lesson 18 Problem Set Answer Key
Question 1.
The following histogram shows the amount of coal produced (by state) for the 20 largest coal-producing states in 2011. Many of these states produced less than 50 million tons of coal, but one state produced over 400 million tons (Wyoming). For the histogram, which one of the three sets of summary measures could match the graph? For each choice that you eliminate, give at least one reason for eliminating the choice.
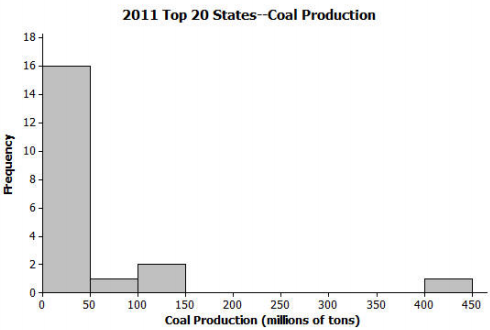
a. Minimum = 1, Q1 = 12, Median = 36, Q3 = 57, Maximum = 410; Mean = 33, MAD = 2.76
b. Minimum = 2, Q1 = 13.5, Median = 27.5, Q3 = 44, Maximum = 439; Mean = 54.6, MAD = 52.36
c. Minimum = 10, Q1 = 37.5, Median = 62, Q3 = 105, Maximum = 439; Mean = 54.6, MAD = 52.36
Answer:
The correct answer is (b).
Choice (a) would not work because Q3 (the average of the 15th and 16th ordered observations) must be less than 50 since both the 15th and 16th ordered observations are less than 50. The mean is most likely greater than (not less than) the median given the skewed right nature of the distribution and the large outlier. The MAD value is most likely much larger than 2.76 given the presence of the outlier and its distance from the cluster of remaining observations.
Choice (c) would not work. Since there are 20 observations, the median (the average of the 10th and 11th ordered observations) must be less than 50, since both the 10th and 11th ordered observations are less than 50. Likewise, the Q3 (the average of the 15th and 16th ordered observations) must be less than 50, since both the 15th and 16th observations are less than 50. The mean is most likely greater than (not less than) the median given the skewed right nature of the distribution and the large outlier.
Question 2.
The heights (rounded to the nearest inch) of the 41 members of the 2012 – 2013 University of Texas Men’s Swimming and Diving Team are shown in the dot plot below.
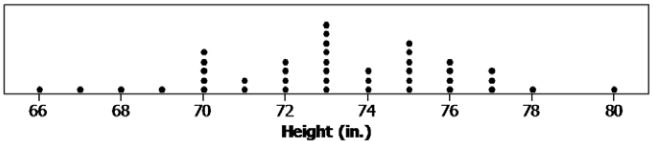
a. Use the dot plot to determine the 5-number summary (minimum, lower quartile, median, upper quartile, and maximum) for the data set.
Answer:
Min = 66, Q1 = 71, Median = 73, Q3 = 75, and Max = 80
b. Based on this dot plot, make a histogram of the heights using the following intervals: 66 to < 68 inches, 68 to < 70 inches, and so on.
Answer:
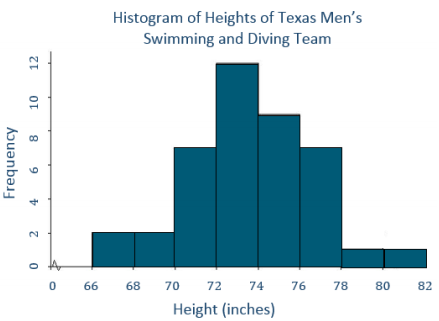
Question 3.
Data on the weight (in pounds) of 143 wild bears are summarized in the histogram below.
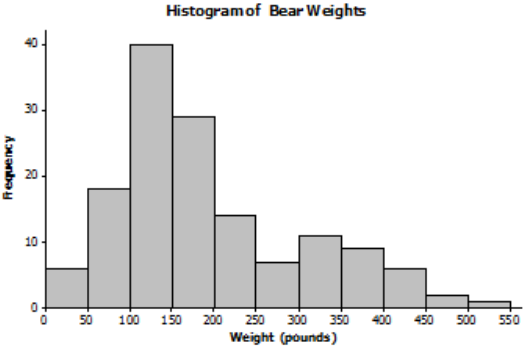
Which one of the three-dot plots below could be a dot plot of the bear weight data? Explain how you determined which the corrected plot.
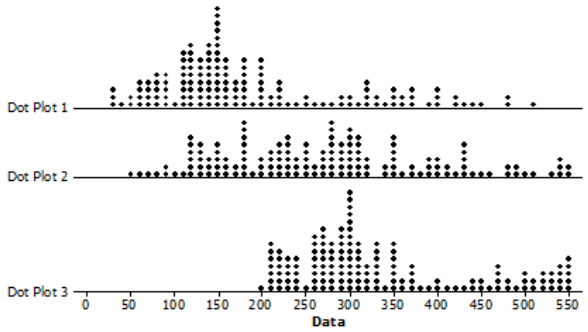
Answer:
Dot plot 1 is the correct choice. Dot plot 2 does not have the same shape as the data distribution shown in the histogram, and it is centered to the right of where the histogram is centered. Although dot plot 3 has the same shape as the distribution shown in the histogram, it is not centered in the same place as the histogram,
Eureka Math Grade 6 Module 6 Lesson 18 Exit Ticket Answer Key
Question 1.
Many states produce maple syrup, which requires tapping sap from a maple tree. However, some states produce more pints of maple syrup per tap than other states. The following dot plot shows the pints of maple syrup yielded per tap in each of the 10 maple syrup-producing states in 2012.

a. Minimum = 0.66, Q1 = 1.26, Median = 1.385, Q3 = 1.71, Maximum = 1.95, Range = 2.4; Mean = 1.95, MAD = 0.28
b. Minimum = 0.66, Q1 = 1.26, Median = 1.71, Q3 = 1.92, Maximum = 1.95, Range = 1.29; Mean = 1.43, MAD = 2.27
c. Minimum = 0.66, Q1 = 1.26, Median = 1.385, Q3 = 1.71, Maximum = 1.95, Range = 1.29; Mean = 1.43, MAD = 0.28
Answer:
The correct answer is (c).
Choice (a) would not work because the range is too large. For the data set, the difference between maximum and minimum is only 1.29 pints. Also, the mean would not be that close to (or the same os) the maximum value in this case.
Choice (b) would not work because a median value of 1.71 would be too high. By estimating the dot values, we see that the 5th and 6th ordered observations (the median for a data set of 10 items) are near 1.4. Also, the MAD is much too large because the range of the data set is only 1.29 pints.
Question 2.
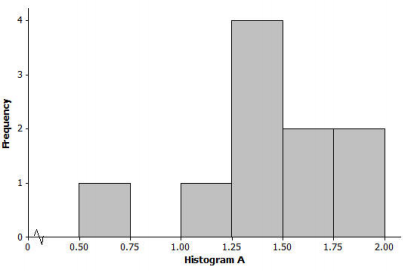
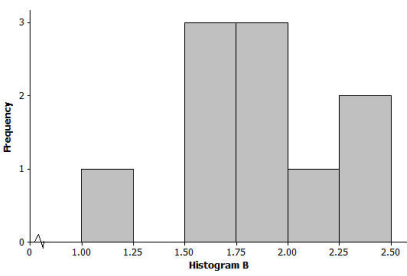
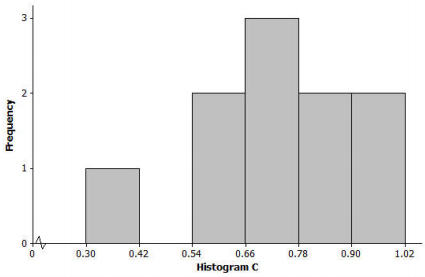
Which one of the three histograms below could be a histogram for the data displayed in the dot plot in Problem 1? For each histogram that you eliminate, give at least one reason for eliminating it as a possibility.
Answer:
The correct answer is the histogram (a).
Histograms (b) and (c) ore for data sets with similar shape features to the correct graph (histogram (a)), but the range and distribution of values do not match the data set in the dot plot. For example, histogram (b) would not be valid, as it is based on 3 data values of 2 pints or more, and there are no values that large in the original dot plot.
Also, the smallest value in the histogram (b) is at least 1 pint, and the actual data set contains a value less than 1 pint. Histogram (c) is based on values that are smaller than many of those in the dot plot; in fact, all of the values in the histogram (c) are less than 1.02 pints, and nearly all of the 10 observations in the actual data set are greater than 1.02.