Engage NY Eureka Math Grade 6 Module 5 Lesson 19 Answer Key
Eureka Math Grade 6 Module 5 Lesson 19 Opening Exercise Answer Key
Opening Exercise:
Question 1.
A box needs to be painted. How many square inches need to be painted to cover the entire surface of the box?
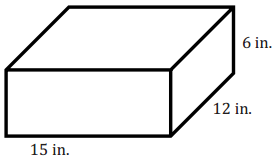
Answer:
SA = 2(15 in.)(12 in.) + 2(15 in.)(6 in.) + 2(12 in.)(6 in.)
SA = 360 in2 + 180 in2 + 144 in2
SA = 684 in2
Question 2.
A juice box is 4 in. tall, 1 in. wide, and 2 in. long. How much juice fits inside the juice box?
Ans;
V = 1 in. × 2 in. × 4 in. = 8 in3
Question 3.
How did you decide how to solve each problem?
Answer:
I chose to use surface area to solve the first problem because you would need to know how much area the paint would need to cover. I chose to use volume to solve the second problem because you would need to know how much space is inside the juice box to determine how much juice it can hold.
Eureka Math Grade 6 Module 5 Lesson 19 Discussion Answer Key
Discussion:
Answer:
Eureka Math Grade 6 Module 5 Lesson 19 Example Answer Key
Example 1:
Vincent put logs in the shape of a rectangular prism outside his house. However, it is supposed to snow, and Vincent wants to buy a cover so the logs stay dry. If the pile of logs creates a rectangular prism with these measurements: 33 cm long, 12 cm wide, and 48 cm high, what is the minimum amount of material needed to cover the pile of logs?
Answer:
→ Where do we start?
We need to find the size of the cover for the logs, so we need to calculate the surface area. in order to find the surface area, we need to know the dimensions of the pile of logs.
→ Why do we need to find the surface area and not the volume?
We want to know the size of the cover Vincent wants to buy. If we calculated volume, we would not have the information Vincent needs when he goes shopping for a cover.
→ What are the dimensions of the pile of logs?
The length is 33 cm, the width is 12 cm, and the height is 48 cm.
→ How do we calculate the surface area to determine the size of the cover?
We can use the surface area formula for a rectangular prism.
SA = 2(33 cm)(12 cm) + 2(33 cm)(48 cm) + 2(12 cm)(48 cm)
SA = 792 cm2 + 3,168 cm2 + 1,152 cm22
SA = 5,112 cm2
→ What is different about this problem from other surface area problems of rectangular prisms you have encountered? How does this change the answer?
If Vincent just wants to cover the wood to keep it dry, he does not need to cover the bottom of the pile of logs. Therefore, the cover can be smaller.
→ How can we change our answer to find the exact size of the cover Vincent needs?
We know the area of the bottom of the pile of logs has the dimensions 33 cm and 12 cm. We can calculate the area and subtract this area from the total surface area.
The area of the bottom of the pile of logs is 396 cm2; therefore, the total surface area of the cover would need to be 5,112 cm2 – 396 cm2 = 4,716 cm2.
Eureka Math Grade 6 Module 5 Lesson 19 Exercise Answer Key
Exercises:
Use your knowledge of volume and surface area to answer each problem.
Exercise 1.
Quincy Place wants to add a pool to the neighborhood. When determining the budget, Quincy Place determined that it would also be able to install a baby pool that requires less than 15 cubic feet of water. Quincy Place has three different models of a baby pool to choose from.
Choke One: 5 ft. × 5 ft. × 1 ft.
ChokeTwo: 4 ft. × 3 ft. × 1 fi
Choke Three: 4 ft. × 2 ft. × 2 ft.
Which of these chokes is best for the baby pool? Why are the others not good choices?
Answer:
Choice One Volume: 5 ft. × 5 ft. × 1 ft. = 25 ft3
Choice Two Volume: 4 ft. × 3 ft. × 1 ft. = 12 ft3
Choice Three Volume: 4 ft. × 2 ft. × 2 ft. = 16 ft3
Choice Two is within the budget because it holds less than 15 cubic feet of water. The other two choices do not work because they require too much water, and Quincy Place will not be able to afford the amount of water it takes to fill the baby pool.
Exercise 2.
A packaging firm has been hired to create a box for baby blocks. The firm was hired because it could save money by creating a box using the least amount of material. The packaging firm knows that the volume of the box must be 18 cm3.
a. What are possible dimensions for the box if the volume must be exactly 18 cm3?
Answer:
Choice 1: 1 cm × 1 cm × 18 cm
Choice 2: 1 cm × 2 cm × 9 cm
Choice 3: 1 cm × 3 cm × 6 cm
Choice 4: 2 cm × 3 cm × 3 cm
b. Which set of dimensions should the packaging firm choose in order to use the least amount of material? Explain.
Answer:
Choice 1: SA = 2(1 cm)(1 cm) + 2(1 cm)(18 cm) + 2(1 cm)(18 cm) = 74 cm2
Choice 2: SA = 2(1 cm)(2 cm) + 2(1 cm)(9 cm) + 2(2 cm)(9 cm) = 58 cm2
Choice 3: SA = 2(1 cm)(3 cm) + 2(1 cm)(6 cm) + 2(3 cm)(6 cm) = 54 cm2
Choice 4: SA = 2(2 cm)(3 cm) + 2(2 cm)(3 cm) + 2(3 cm)(3 cm) = 42 cm2
The packaging firm should choose Choice 4 because it requires the least amount of material. in order to find the amount of material needed to create a box,, the packaging firm would have to calculate the surface area of each box. The box with the smallest surface area requires the least amount of material.
Exercise 3.
A gift has the dimensions of 50 cm × 35 cm × 5 cm. You have wrapping paper with dimensions of 75 cm × 60 cm. Do you have enough wrapping paper to wrap the gift? Why or why not?
Answer:
Surface Area of the Present SA = 2(50 cm)(35 cm) + 2(50 cm)(5 cm) + 2(35 cm)(5 cm) = 3,500 cm2 + 500 cm2 + 350 cm2 = 4,350cm2
Area of Wrapping Paper: A = 75 cm × 60 cm = 4,500 cm2
I do have enough paper to wrap the present because the present requires 4,350 square centimeters of paper, andi
have 4,500 square centimeters of wrapping paper.
Exercise 4.
Tony bought a flat-rate box from the post office to send a gift to his mother for Mother’s Day. The dimensions of the medium-size box are 14 inches × 12 inches × 3.5 inches. What is the volume of the largest gift he can send to his mother?
Answer:
Volume of the Box: V = 14 in. × 12 in. × 3.5 in. = 588 in3
Tony would have 588 cubic inches of space to fill with a gift for his mother.
Exercise 5.
A cereal company wants to change the shape of its cereal box in order to attract the attention of shoppers. The original cereal box has dimensions of 8 inches × 3 inches × 11 inches. The new box the cereal company is thinking of would have dimensions of 10 inches × 10 inches × 3 inches.
a. Which box holds more cereal?
Answer:
Volume of Original Box: V = 8 in. × 3 in. × 11 in. = 264 in3
Volume of New Box: V= 10 in. × 10 in. × 3 in.= 300 in3
The new box holds more cereal because it has a larger volume.
b. Which box requires more material to make?
Answer:
Surface Area of Original Box: SA = 2(8 in.)(3 in.) + 2(8 in.)(11 in.)+ 2(3 in.)(11 in.) = 48 in2 + 176 in2 + 66 in2 = 290 in2
Surface Area of New Box: SA = 2(10 in.)(10 in.) + 2(10 in.)(3 in.) + 2(10 in.)(3 in.) = 200 in2 + 60 in2 + 60 in2 = 320 in2
The new box requires more material than the original box because the new box has a larger surface area.
Exercise 6.
Cinema theaters created a new popcorn box in the shape of a rectangular prism. The new popcorn box has a length of 6 inches, a width of 3. 5 inches, and a height of 3.5 inches but does not include a lid.
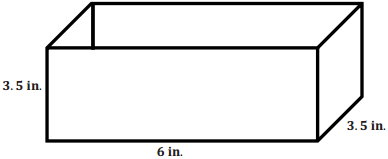
a. How much material is needed to create the box?
Answer:
Surface Area of the Box: SA = 2(6 in.)(3. 5 in.) + 2(6 in.)(3.5 in.) + 2(3.5 in.)(3. 5 in.) = 42 in2 + 42 in2 + 24.5 in2 = 108.5 in2
The box does not have a lid, so we have to subtract the area of the lid from the surface area.
Area of Lid: 6 in. × 3.5 in. = 21 in2
Total Surface Area: 108.5 in2 – 21 in2 = 87.5 in2
87.5 square inches of material is needed to create the new popcorn box.
b. How much popcorn does the box hold?
Answer:
Volume of the Box: V= 6 in. × 3.5 in. × 3.5 in. = 73.5 in3
The box holds 73.5 in3 of popcorn.
Eureka Math Grade 6 Module 5 Lesson 19 Problem Set Answer Key
Solve each problem below.
Question 1.
Dante built a wooden, cubic toy box for his son. Each side of the box measures 2 feet.
a. How many square feet of wood did he use to build the box?
Answer:
Surface Area of the Box: SA = 6(2 ft)2 = 6(4 ft2) = 24 ft2
Dante used 24 square feet of wood to build the box.
b. How many cubic feet of toys will the box hold?
Answer:
Volume of the Box: V = 2 ft. × 21 ft. × 2 ft.= 8 ft3
The toy box would hold 8 cubic feet of toys.
Question 2.
A company that manufactures gift boxes wants to know how many different-sized boxes having a volume of 50 cubic centimeters it can make if the dimensions must be whole centimeters.
a. List all the possible whole number dimensions for the box.
Answer:
Choice One: 1 cm × 1 cm × 50 cm
Choice Two: 1 cm × 2 cm × 25 cm
Choice Three: 1 cm × 5 cm × 10 cm
Choice Four: 2 cm × 5 cm × 5 cm
b. Which possibility requires the least amount of material to make?
Answer:
Choice One: SA = 2(1 cm)(1 cm) + 2(1 cm)(50 cm) + 2(1 cm)(50 cm) = 2 cm2 + 100 cm2 + 100 cm2 = 202 cm2
Choice Two: SA = 2(1 cm)(2 cm) + 2(1 cm)(25 cm) + 2(2 cm)(25 cm) = 4 cm2 + 50 cm2 + 100 cm2 = 154 cm2
Choice Three: SA = 2(1 cm)(5 cm) + 2(1 cm)(10 cm) + 2(5 cm)(10 cm) = 10 cm2 + 20 cm2 + 100 cm2 = 130 cm2
Choice Four: SA = 2(2 cm)(5 cm) + 2(2 cm)(5 cm) + 2(5 cm)(5 cm) = 20 cm2 + 20 cm2 + 50 cm2 = 90 cm2
Choice Four requires the least amount of material because it has the smallest surface area.
c. Which box would you recommend the company use? Why?
Answer:
I would recommend the company use the box with dimensions of 2 cm × 5 cm × 5 cm (Choice Four) because it requires the least amount of material to make, so it would cost the company the least amount of money to make.
Question 3.
A rectangular box of rice is shown below. What is the greatest amount of rice, in cubic inches, that the box can hold?
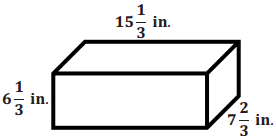
Answer:
Volume of the Rice Box: V = 15\(\frac{1}{3}\) in. × 7\(\frac{2}{3}\) in. × 6\(\frac{1}{3}\) in. = \(\frac{20,102}{27}\) in3 = 744\(\frac{14}{27}\) in3
Question 4.
The Mars Cereal Company has two different cereal boxes for Mars Cereal. The large box is 8 inches wide, 11 inches high, and 3 inches deep. The small box is 6 inches wide, 10 inches high, and 2.5 inches deep.
a. How much more cardboard is needed to make the large box than the small box?
Answer:
SurfaceArea of the Large Box: SA = 2(8 in.)(11 in.) + 2(8 in.)(3 in.) + 2(11 in.)(3 in.) = 176 in2 + 48 in2 +66 in2 = 290 in2
Surface Area of the Small Box: SA = 2(6 in. )(10 in.) + 2(6 in.)(2. 5 in.) + 2(10 in. )(2. 5 in.) = 120 in2 + 30 in2 + 50 in2 = 200 in2
Difference: 290 in2 – 200 in2 = 90 in2
The large box requires 90 square inches more cardboard than the small box.
b. How much more cereal does the large box hold than the small box?
Answer:
Volume of the Large Box: V = 8 in. × 11 in. × 3 in. = 264 in3
Volume of the Small Box: V = 6 in. × 10 in. × 2.5 in. = 150 in3
Difference: 264 in3 – 150 in3 = 114 in3
The large box holds 114 cubic inches more cereal than the small box.
Question 5.
A swimming pool is 8 meters long, 6 meters wide, and 2 meters deep. The water-resistant paint needed for the pool costs $6 per square meter. How much will it cost to paint the pool?
a. How many faces of the poo1 do you have to paint?
Answer:
You have to point 5 faces.
b. How much paint (in square meters) do you need to paint the pool?
Answer:
SA = 2(8 m × 6 m) + 2(8 m × 2 m) + 2(6 m × 2 m) = 96 m2 + 32 m2 + 24 m2 = 152 m2
Area of Top of Pool: 8 m × 6 m= 48 m2
Total Point Needed: 152 m2 – 48 m2 = 104 m2
c. How much will it cost to paint the pool?
Answer:
104 m2 × $6/m2 = $624
It will cost $624 to point the pool.
Question 6.
Sam is in charge of filling a rectangular hole with cement. The hole is 9 feet long, 3 feet wide, and 2 feet deep. How much cement will Sam need?
Answer:
V = 9 ft. × 3 ft. × 2 ft. = 54 ft3
Sam will need 54 cubic feet of cement to fill the hole.
Question 7.
The volume of Box D subtracted from the volume of Box C is 23.14 cubic centimeters. Box D has a volume of 10.115 cubic centimeters.
a. Let C be the volume of Box C in cubic centimeters. Write an equation that could be used to determine the volume of Box C.
Answer:
C – 10.115 cm3 = 23.14 cm3
b. Solve the equation to determine the volume of Box C.
Answer:
C – 10.115 cm3 + 10.115 cm3 = 23.14 cm3 + 10.115 cm3
C = 33. 255 cm3
c. The volume of Box C is one-tenth of the volume of another box, Box E. Let E represent the volume of Box E in cubic centimeters. Write an equation that could be used to determine the volume of Box E, using the result from part (b).
Answer:
33.255 cm3 = \(\frac{1}{10}\)E
d. Solve the equation to determine the volume of Box E.
Answer:
33.255cm3 ÷ \(\frac{1}{10}\) = \(\frac{1}{10}\)E ÷ \(\frac{1}{10}\)
332.55 cm3 = E
Eureka Math Grade 6 Module 5 Lesson 19 Exit Ticket Answer Key
Solve the word problem below.
Question 1.
Kelly has a rectangular fish aquarium that measures 18 inches long. 8 inches wide, and 12 inches tall.
a. What is the maximum amount of water the aquarium can hold?
Answer:
Volume of the Aquarium: V = 18 in. × 8 in. × 12 in. = 1,728 in3
The maximum amount of water the aquarium can hold is 1, 728 cubic inches.
b. If Kelly wanted to put a protective covering on the four glass walls of the aquarium, how big does the cover have to be?
Answer:
Surface Area of theAquarium: SA = 2(18 in.)(8 in.)+ 2(18 in.)(12 in.)+ 2(8 in.)(12 in.) = 288 in2 + 432 in2 + 192 in2 = 912 in2
We only need to cover the four glass walls, so we can subtract the area of both the top and bottom of the aquarium.
Area of Top: A = 18 in. × 8 in. = 144 in2
Area of Bottom: A = 18 in. × 8 in. = 144 in2
Surface Area of the Four Walls: SA = 912 in2 – 144 in2 – 144 in2 = 624 in2
Kelly would need 624 in2 to cover the four walls of the aquarium.
Eureka Math Grade 6 Module 5 Lesson 19 Area of shapes Answer Key
Area of shapes:
Question 1.
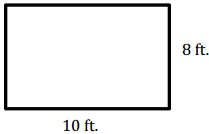
Answer:
A = 80 ft2
Question 2.
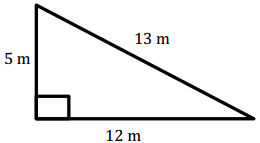
Answer:
A = 30 m2
Question 3.
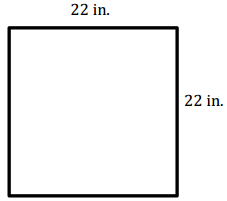
Answer:
A = 484 in2
Question 4.
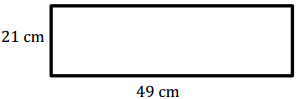
Answer:
A = 1,029 cm2
Question 5.
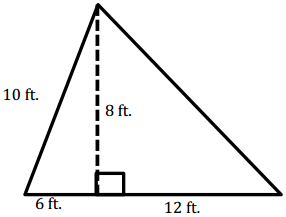
Answer:
A = 72 ft2
Question 6.
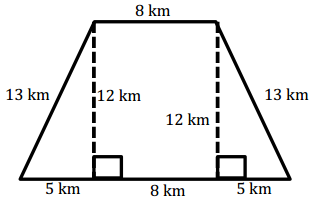
Answer:
A = 156 km2
Question 7.
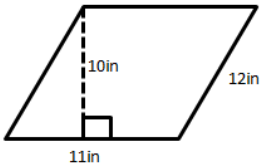
Answer:
A = 110 in2
Question 8.
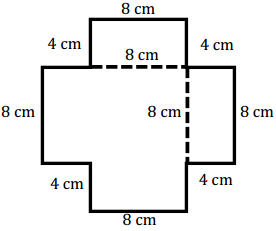
Answer:
A = 192 cm2
Question 9.
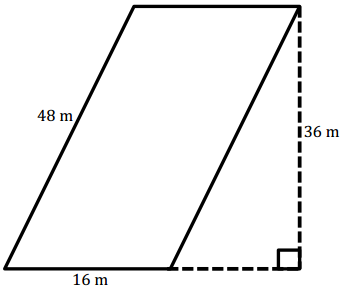
Answer:
A = 576 m2
Question 10.

Answer:
A = 1,476 ft2