Engage NY Eureka Math Grade 6 Module 5 Lesson 14 Answer Key
Eureka Math Grade 6 Module 5 Lesson 14 Example Answer Key
Example 1:
a. The area of the base of a sandbox is 9\(\frac{1}{2}\) ft2. The volume of the sandbox is 7\(\frac{1}{8}\) ft3. Determine the height of the sandbox.

Answer:
→ What information are we given in this problem?
We have been given the area of the base and the volume.
→ How can we use the information to determine the height?
We know that the area of the base times the height gives the volume. Since we already have the volume, we can do the opposite and divide to get the height.
Notice that the number for the volume is less than the number for the area.
→ What does that tell us about the height?
If the product of the area of the base and the height is less than the area, we know that the height must be less than 1.
→ Calculate the height by solving a one-step equation.
Volume = Area of the base × height
V = bh
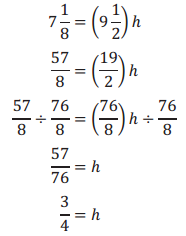
The height of the sandbox is \(\frac{3}{4}\) ft.
→ We could also calculate the height using the equation Height = Volume ÷ Area of the base. Solve using this equation to determine if the height will be the same.
Height = Volume ÷ Area of the base
h = V ÷ b
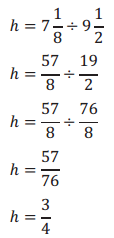
The height of the sandbox is \(\frac{3}{4}\) ft.
b. The sandbox was filled with sand, but after the kids played, some of the sand spilled out. Now, the sand is at a height of \(\frac{1}{2}\) ft. Determine the volume of the sand in the sandbox after the children played in it.
Answer:
→ What new information have we been given in this problem?
This means that the sandbox is not totally filled. Therefore, the volume of sand used is not the same as the volume of the sandbox.
→ How will we determine the volume of the sand?
To determine the volume of the sand, I use the area of the base of the sandbox, but I use the height of \(\frac{1}{2}\)ft. instead of the height of the sandbox.
Volume = Area of the base × height
Volume = 9\(\frac{1}{2}\) ft2 × \(\frac{1}{2}\) ft.
Volume = \(\frac{19}{2}\) ft2 × \(\frac{1}{2}\) ft.
Volume = \(\frac{19}{4}\) ft3
Volume = 4\(\frac{3}{4}\) ft3
The volume of the sand is 4\(\frac{3}{4}\) ft3.
Example 2:
A special-order sandbox has been created for children to use as an archeological digging area at the zoo. Determine the volume of the sandbox.
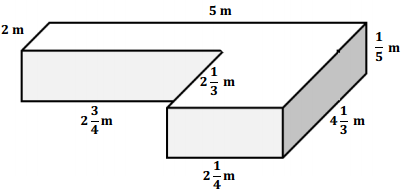
Answer:
→ Describe this three-dimensional figure.
This figure looks like two rectangular prisms that have been placed together to form one large prism.
I could think of it as a piece on the left and a piece on the right.
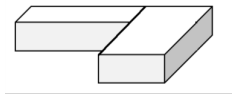
→ Or, I could think of it as a piece in front and a piece behind.
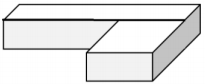
→ How can we determine the volume of this figure?
We can find the volume of each piece and then add the volumes together to get the volume of the entire figure.
→ Does it matter which way we divide the shape when we calculate the volume?
Answers will vary.
→ At this point, you can divide the class in half and have each half determine the volume using one of the described methods.
If the shape is divided into a figure on the left and a figure on the right, we would have the following:
Volume of prism on the left = l w h.
V = 2\(\frac{3}{4}\) m × 2 m × \(\frac{1}{5}\) m
V = \(\frac{11}{4}\) m × 2 m × \(\frac{1}{5}\) m
V = \(\frac{22}{20}\) m3
→ Volume of the prism on the right = l w h.
V = 2\(\frac{1}{4}\) m × 4\(\frac{1}{3}\) m × \(\frac{1}{5}\) m
V = \(\frac{9}{4}\) m × \(\frac{13}{3}\) m × \(\frac{1}{5}\) m
V = \(\frac{117}{60}\) m
V = \(\frac{39}{20}\) m3
Total volume = volume of left + volume of right
Total volume = \(\frac{22}{20}\) m3 + \(\frac{39}{20}\) m3
Total volume = \(\frac{61}{20}\) m3 = 3\(\frac{1}{20}\) m3
If the shape is divided into a figure with a piece in front and piece behind, we have the following:
Volume of the back piece = l w h
V = 5 m × 2 m × \(\frac{1}{5}\) m
V = 2m3
Volume of the front piece = l w h
V = 2\(\frac{1}{4}\) m × 2\(\frac{1}{3}\) m × \(\frac{1}{5}\) m
V = \(\frac{9}{4}\) m × \(\frac{7}{3}\) m × \(\frac{1}{5}\) m
V = \(\frac{63}{60}\) m3 = 1\(\frac{3}{60}\) m = 1\(\frac{1}{20}\) m3
Total volume = volume of back + volume of front
Total volume = 2 m3 + 1\(\frac{1}{20}\) m3
Total volume = 3\(\frac{1}{20}\) m3
→ What do you notice about the volumes determined in each method?
The volume calculated with each method is the same. It does not matter how we break up the shape. We still get the same volume.
Eureka Math Grade 6 Module 5 Lesson 14 Exercise Answer Key
Exercise 1.
a. The volume of the rectangular prism is \(\frac{36}{15}\) yd3. Determine the missing measurement using a one-step equation.
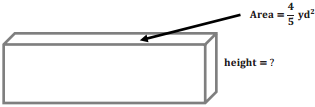
Answer:
V = bh
\(\frac{36}{15}\) = \(\frac{4}{5}\) h
\(\frac{36}{15}\) ÷ \(\frac{12}{15}\) = \(\frac{12}{15}\)h ÷ \(\frac{12}{15}\)
\(\frac{36}{12}\) = h
3 = h
The height is 3 yd.
b. The volume of the box is \(\frac{45}{6}\) m3. Determine the area of the base using a one-step equation.
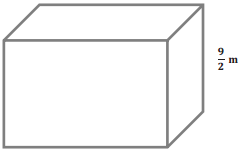
Answer:
V = bh
\(\frac{45}{6}\) = b(\(\frac{2}{9}\))
\(\frac{45}{6}\) ÷ \(\frac{27}{6}\) = b(\(\frac{27}{6}\)) ÷ \(\frac{7}{6}\)
\(\frac{45}{27}\) = b
\(\frac{5}{3}\) = b
The area of the base is \(\frac{45}{6}\) m2.
Exercise 2.
Marissa’s fish tank needs to be filled with more water.
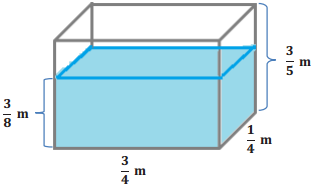
a. Determine how much water the tank can hold.
Answer:
Volume of entire tank = l w h
V = (\(\frac{3}{4}\) m) (\(\frac{1}{4}\) m) (\(\frac{3}{5}\) m)
V = \(\frac{9}{80}\) m3.
b. Determine how much water is already in the tank.
Answer:
Volume of water in the tank = l w h
V = (\(\frac{3}{4}\) m) (\(\frac{1}{4}\) m) (\(\frac{3}{8}\) m)
V = \(\frac{9}{128}\) m3.
c. How much more water is needed to fill the tank?
Answer:
Height of empty part of tank:
h = \(\frac{3}{5}\) m – \(\frac{3}{8}\) m
= \(\frac{24}{40}\) m – \(\frac{15}{40}\) m
= \(\frac{9}{40}\) m
Volume needed to fill = l w h
V = (\(\frac{3}{4}\) m) (\(\frac{1}{4}\) m) (\(\frac{9}{40}\) m)
V = \(\frac{27}{640}\) m3
Exercise 3.
Determine the volume of composite figures.
a. 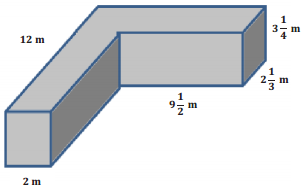
Answer:
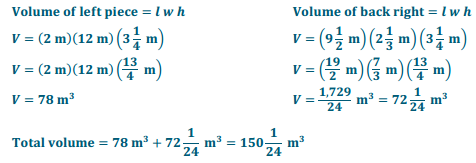
b. 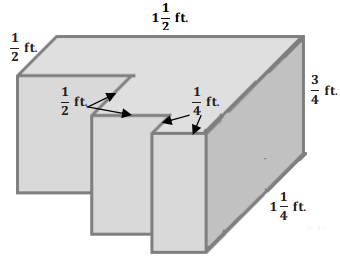
Answer:
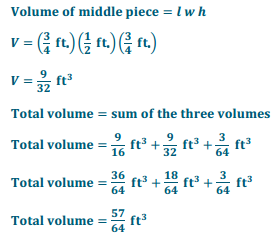
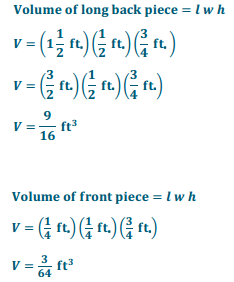
Another possible solution:
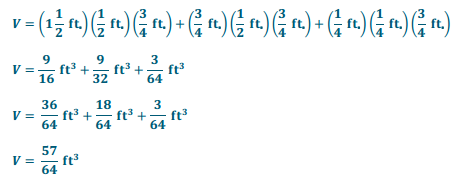
Eureka Math Grade 6 Module 5 Lesson 14 Problem Set Answer Key
Question 1.
The volume of a rectangular prism is \(\frac{21}{12}\) ft3, the height of the prism is \(\frac{3}{4}\) ft. Determine the area of the base.
Answer:
V = bh
\(\frac{21}{12}\) = b (\(\frac{3}{4}\))
\(\frac{21}{9}\) = b
The area of the base is \(\frac{21}{9}\) ft2 OR \(\frac{7}{3}\) ft2.
Question 2.
The volume of a rectangular prism is \(\frac{10}{21}\) ft3. The area of the base is \(\frac{2}{3}\) ft2. Determine the height of the rectangular prism.
Answer:
Height = Volume ÷ Area of the base
Helght = \(\frac{10}{21}\) ft3 ÷ \(\frac{2}{3}\) ft2
Height = \(\frac{10}{21}\) ft3 ÷ \(\frac{14}{21}\) ft2
Height = \(\frac{10}{14}\) ft. OR \(\frac{5}{7}\) ft.
Question 3.
Determine the volume of the space in the tank that still needs to be tilled with water if the water is ft. deep.

Answer:
Volume of tank = l w h
Volume of tank = (5 ft.) (1\(\frac{2}{3}\) ft.) (2 ft.)
Volume of tank = \(\frac{50}{3}\) ft3
Volume to be filled = \(\frac{50}{3}\) ft3 – \(\frac{25}{9}\) ft3
Volume to be filled = \(\frac{150}{9}\) ft3 – \(\frac{25}{9}\) ft3
Volume to be filled = \(\frac{125}{9}\) ft3
Volume of water = l w h
VoIumeofwater = (5 ft.) (1\(\frac{2}{3}\) ft.) (\(\frac{1}{3}\) ft.)
Volume of water = \(\frac{25}{9}\) ft3
Question 4.
Determine the volume of composite figure.
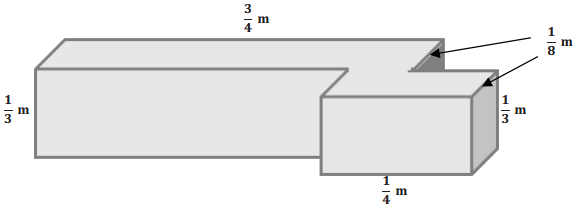
Answer:
Volume of back piece = l w h
Volume of back piece = (\(\frac{3}{4}\) m) (\(\frac{1}{8}\) m) (\(\frac{1}{3}\) m)
Volume of back piece = \(\frac{3}{96}\) m3
Volume of front piece = l w h
Volume of front piece = (\(\frac{1}{4}\) m) (\(\frac{1}{8}\) m) (\(\frac{1}{3}\) m)
Volume of front piece = \(\frac{1}{96}\) m3
Total volume = \(\frac{3}{96}\) m3 + \(\frac{1}{96}\) m3 = \(\frac{4}{96}\) m3 OR \(\frac{1}{24}\)m3
Question 5.
Determine the volume of the composite figure.
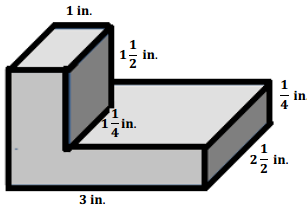
Answer:
V = (1 in.) (1\(\frac{1}{2}\) in.) (1\(\frac{1}{4}\) in.) + (3 in.) (2\(\frac{1}{2}\) in.) (\(\frac{1}{4}\) in.)
V = (1 in.) (\(\frac{3}{2}\) in.) (\(\frac{5}{4}\) in.) + (3 in.) (\(\frac{5}{2}\) in.) (\(\frac{1}{4}\) in.)
V = \(\frac{15}{8}\) in3 + \(\frac{15}{8}\) in3
V = \(\frac{30}{8}\) in3 = 3\(\frac{6}{8}\) in3 OR 3\(\frac{3}{4}\) in3
Question 6.
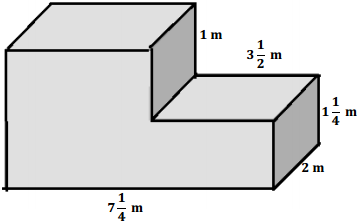
a. Write an equation to represent the volume of the composite figure.
Answer:
V = (3\(\frac{1}{2}\) m × 2 m × 1\(\frac{1}{4}\) m) + (3\(\frac{3}{4}\) m × 2 m × 2\(\frac{1}{4}\) m)
b. Use your equation to calculate the volume of the composite figure.
Answer:
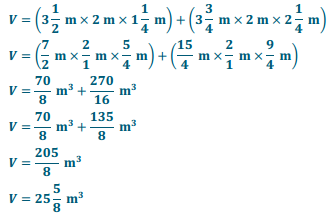
Eureka Math Grade 6 Module 5 Lesson 14 Exit Ticket Answer Key
Question 1.
Determine the volume of the water that would be needed to fill the rest of the tank.
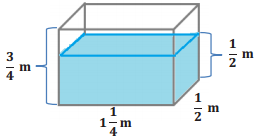
Answer:
Volume of tank = l w h
Volume of tank = (1\(\frac{1}{4}\) m) (\(\frac{1}{2}\) m) (\(\frac{3}{4}\) m)
Volume of tank = \(\frac{15}{32}\) m3
Volume of water = l w h
Volume of water = (1\(\frac{1}{4}\) m) (\(\frac{1}{2}\) m) (\(\frac{1}{2}\) m)
Volume of waler = \(\frac{5}{16}\) m3 = \(\frac{10}{32}\) m
Remaining water needed = \(\frac{15}{32}\) m3 – \(\frac{10}{32}\) m3 = \(\frac{5}{32}\)m3
Question 2.
Determine the volume of the composite figure.
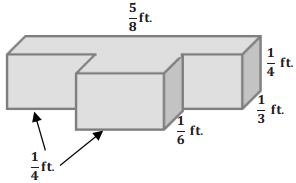 Answer:
Answer:
Volume of back piece = l w h
Volume of back piece = (\(\frac{5}{8}\) ft.) (\(\frac{1}{3}\) ft.) (\(\frac{1}{4}\) ft.)
Volume of back piece = \(\frac{5}{96}\) ft3
Volume of front piece = l w h
Volume of front piece = (\(\frac{1}{4}\) ft.) (\(\frac{1}{6}\) ft.) (\(\frac{1}{4}\) ft.)
Volume of front piece = \(\frac{1}{96}\) ft3
Total volume = \(\frac{5}{96}\) ft3 + \(\frac{1}{96}\) ft3 = \(\frac{6}{96}\) ft3 = \(\frac{2}{32}\) ft3