Engage NY Eureka Math 6th Grade Module 4 Lesson 20 Answer Key
Eureka Math Grade 6 Module 4 Lesson 20 Example Answer Key
Example 1.
The farmers’ market is selling bags of apples. In every bag, there are 3 apples.
a. Complete the table
| Number of Bags | Total Number of Apples |
| 1 | 3 |
| 2 | |
| 3 | |
| 4 | |
| B |
Answer:
| Number of Bags | Total Number of Apples |
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| B | 3B |
b. What if the market had 25 bags of apples to sell? How many apples is that in all?
Answer:
If B = 25, then 3B = 3 25 = 75. The market had 75 apples to sell.
c. If a truck arrived that had some number, a, more apples on it, then how many bags would the clerks use to bag up the apples?
Answer:
a ÷ 3 bags are needed. If there are 1 or 2 apples left over, an extra bag will be needed (although not full).
d. If a truck arrived that had 600 apples on It, how many bags would the clerks use to bag up the apples?
apples
Answer:
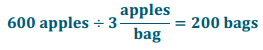
e. How is part (d) different from part (b)?
Answer:
Part (d) gives the number of apples and asks for the number of bags. Therefore, we needed to divide the number of apples by 3. Part (b) gives the number of bags and asks for the number of apples. Therefore, we needed to multiply the number of bags by 3.
Eureka Math Grade 6 Module 4 Lesson 20 Exercise Answer Key
Exercise 1.
In New York State, there is a five-cent deposit on all carbonated beverage cans and bottles. When you return the empty can or bottle, you get the five cents back.
a. Complete the table.
| Number of Containers Returned | Refund in Dollars |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 10 | |
| 50 | |
| 100 | |
| C |
Answer:
| Number of Containers Returned | Refund in Dollars |
| 1 | 0.05 |
| 2 | 0.10 |
| 3 | 0.15 |
| 4 | 0.20 |
| 10 | 0.50 |
| 50 | 2.50 |
| 100 | 5.00 |
| C | 0.05C |
b. If we let C represent the number of cans, what is the expression that shows how much money is returned?
Answer:
0.05c
c. Use the expression to find out how much money Brett would receive if he returned 222 cans.
Answer:
if c = 222, then 0. 05C = 0.05 ? 222 = 11.10. Brett would receive $11. 10 if he returned 222 cans.
d. If Gavin needs to earn $4. 50 for returning cans, how many cans does he need to collect and return?
Answer:
4.50 ÷ 0.05 = 90. Gavin needs to collect and return 90 cans.
e. How is part (d) different from part (c)?
Answer:
Part (d) gives the amount of money and asks for the number of cans. Therefore, we needed to divide the amount of money by 0.05. Part (c) gives the number of cans and asks for the amount of money. Therefore, we needed to multiply the number of cans by 0.05.
Exercise 2.
The fare for a subway or a local bus ride is $2. 50.
a. Complete the table.
| Number of Rides | Cost of Rides in Dollars |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 10 | |
| 30 | |
| R |
Answer:
| Number of Rides | Cost of Rides in Dollars |
| 1 | 2.50 |
| 2 | 5.00 |
| 3 | 7.50 |
| 4 | 10.00 |
| 5 | 12.50 |
| 10 | 25.00 |
| 30 | 75.00 |
| R | 2.50 R or 2.5 R |
b. If we let R represent the number of rides, what is the expression that shows the cost of the rides?
Answer:
2.50R or 2. 5R
c. Use the expression to find out how much money 60 rides would cost.
Answer:
If R = 60, then 2.50R = 2.50 ∙ 60 = 150.00. Sixty rides would cost $150.00.
d. If a commuter spends $175.00 on subway or bus rides, how many trips did the commuter take?
Answer:
175.00 ÷ 2.50 = 70. The commuter took 70 trips.
e. How is part (d) different from part (c)?
Answer:
Part (d) gives the amount of money and asks for the number of rides. Therefore, we needed to divide the
amount of money by the cost of each ride ($2. 50). Part (c) gives the number of rides and asks for the amount of money. Therefore, we needed to multiply the number of rides by $2. 50.
Challenge Problem
Exercise 3.
A pendulum swings though a certain number of cycles in a given time. Owen made a pendulum that swings 12 times every 15 seconds.
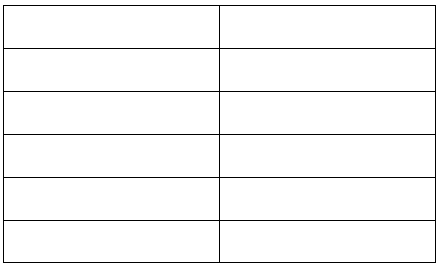
a. Construct a table showing the number of cycles through which a pendulum swings. Include data for up to one minute. Use the last row for C cycles, and write an expression for the time it takes for the pendulum to make C cycles.
Answer:
| Number of Cycles | Time in seconds |
| 12 | 15 |
| 24 | 30 |
| 36 | 45 |
| 48 | 60 |
| C | \( \frac{15 C}{12} \) |
b. Owen and his pendulum team set their pendulum in motion and counted 16 cycles. What was the elapsed time?
Answer:
C = 16; \(\frac{15 \cdot 16}{12}\) = 20. The elapsed time is 20 seconds.
c. Write an expression for the number of cycles a pendulum swings in S seconds.
Answer:
\(\frac{12}{15}\)S or \(\frac{4}{5}\)S or 0.8 ∙ S
d. In a different experiment, Owen and his pendulum team counted the cycles of the pendulum for iS seconds. How many cycles did they count?
Answer:
S = 35; 0.8 ∙ 35 = 28. They counted 28 cycles.
Eureka Math Grade 6 Module 4 Lesson 20 Problem Set Answer Key
Question 1.
A radio station plays 12 songs each hour. They never stop for commercials, news, weather, or traffic reports.
a. Write an expression describing how many songs are played by the radio station in H hours.
Answer:
12H
b. How many songs will be played ¡n an entire day (24 hours)?
Answer:
12 ∙ 24 = 288. There will be 288 songs played.
c. How long does it take the radio station to play 60 consecutive songs?
Answer:
![]()
Question 2.
A ski area has a high-speed lift that can move 2,400 skiers to the top of the mountain each hour.
a. Write an expression describing how many skiers can be lifted in H hours.
Answer:
2,400H
b. How many skiers can be moved to the top of the mountain in 14 hours?
Answer:
14 ∙ 2,400 = 33,600. 33,600 skiers can be moved.
c. How long will it take to move 3,600 skiers to the top of the mountain?
Answer:
3,600 ÷ 2,400 = 1.5. It will take an hour and a half to move 3,600 skiers to the top of the mountain.
Question 3.
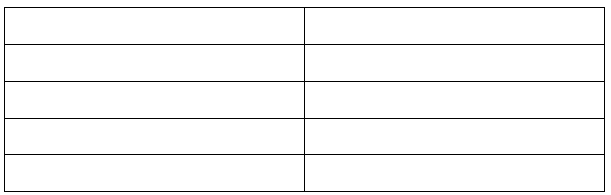
Polly writes a magazine column, for which she earns $35 per hour. Create a table of values that shows the relationship between the number of hours that Polly works, H, and the amount of money Polly earns in dollars, E.
Answer:
Answers will vary. Sample answers are shown.
| Hours Polly Works (H) | Polly’s Earnings in Dollars |
| 1 | 35 |
| 2 | 70 |
| 3 | 105 |
| 4 | 140 |
a. If you know how many hours Polly works, can you determine how much money she earned? Write the
corresponding expression.
Answer:
Multiplying the number of hours that Polly works by her rate ($35 per hour) will calculate her pay. 35H ¡s the expression for her pay in dollars.
b. Use your expression to determine how much Polly earned after working for 3\(\frac { 1 }{ 2 }\) hours.
Answer:
35H = 35 ∙ 3.5 = 122.5. Polly makes $122. 50 for working 3\(\frac{1}{2}\) hours.
c. If you know how much money Polly earned, can you determine how long she worked? Write the corresponding expression.
Answer:
Dividing Polly’s pay by 35 will calculate the number of hours she worked. E ÷ 35 ¡s the expression for the
number of hours she worked.
d. Use your expression to determine how long Polly worked if she earned $52. 50.
Answer:
52.50 – 35 = 1.5; Polly worked on hour and a half for $52.50.
Question 4.
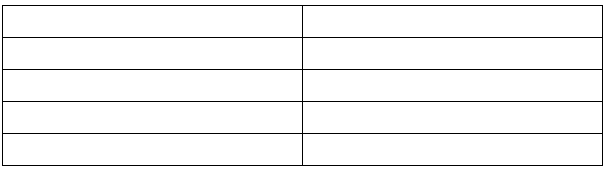
Mitchell delivers newspapers after school, for which he earns $0.09 per paper. Create a table of values that shows the relationship between the number of papers that Mitchell delivers, P, and the amount of money Mitchell earns in dollars, E.
Answer:
Answers will vary. Sample answers are shown.
| Numbers of papers Delivered (P) | Mitchell’s Earnings in Dollars (E) |
| 1 | 0.09 |
| 10 | 0.90 |
| 100 | 9.00 |
| 1,000 | 90.00 |
a. If you know how many papers Mitchell delivered, can you determine how much money he earned? Write the corresponding expression.
Answer:
Multiplying the number of papers that Mitchell delivers by his rate ($0.09 per paper) will calculate his pay. 0. 09P is the expression for his pay in dollars.
b. Use your expression to determine how much Mitchell earned by delivering 300 newspapers.
Answer:
0. 09P = 0. 09 ∙ 300 = 27. Mitchell earned $27. 00 for delivering 300 newspapers.
c. If you know how much money Mitchell earned, can you determine how many papers he delivered? Write the corresponding expression.
Answer:
Dividing Mitchell’s pay by $0.09 will calculate the number of papers he delivered. E ÷ 0.09 Is the expression for the number of papers he delivered.
d. Use your expression to determine how many papers Mitchell delivered if he earned $58. 50 last week.
Answer:
58.50 ÷ 0.09 = 650; therefore, Mitchell delivered 650 newspapers last week.
Question 5.
Randy is an art dealer who sells reproductions of famous paintings. Copies of the Mona Lisa sell for $475.
a. Last year Randy sold $9, 975 worth of Mona Lisa reproductions. How many did he sell?
Answer:
9,975 ÷ 475 = 21. He sold 21 copies of the painting.
b. If Randy wants to increase his sales to at least $15,000 this year, how many copies will he need to sell (without changing the price per painting)?
Answer:
15,000 ÷ 475 is about 31.6. He will have to sell 32 paintings in order to increase his sales to at least $15,000.
Eureka Math Grade 6 Module 4 Lesson 20 Exit Ticket Answer Key
Anna charges $8. 50 per hour to babysit. Complete the table, and answer the questions below.
| Numbers of hours | Amount Anna Charges in Dollars |
| 1 | |
| 2 | |
| 5 | |
| 8 | |
| H |
Answer:
| Numbers of hours | Amount Anna Charges in Dollars |
| 1 | 8.50 |
| 2 | 17.00 |
| 5 | 42.50 |
| 8 | 68 |
| H | 8.50H or 8.5H |
a. Write an expression describing her earnings for working H hours.
Answer:
8.50H or 8.5H
b How much will she earn if she works for 3 hours?
Answer:
If H = 3.5, then 8.5H = 8.5 ∙ 3.5 = 29.75. She will earn $29.75.
c. How long will it take Anna to earn $51.00?
Answer:
51 ÷ 8.5 = 6. It will take Anna 6 hours to earn $51.00.