Eureka Math Grade 6 Module 4 Lesson 11 Answer Key

Engage NY Eureka Math 6th Grade Module 4 Lesson 11 Answer Key

Eureka Math Grade 6 Module 4 Lesson 11 Example Answer Key

a. Use the model to answer the following questions.

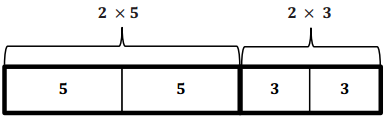
How many fives are in the model?
Answer:
5

How many threes are In the model?
Answer:
2

What does the expression represent in words?
Answer:
The sum of two groups of five and two groups of three

What expression could we write to represent the model?
Answer:
2 × 5 + 2 × 3

b. Use the new model and the previous model to answer the next set of questions.

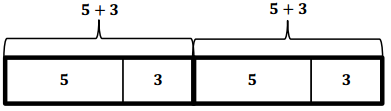
How many fives are in the model?
Answer:
2

How many threes are in the model?
Answer:
2

What does the expression represent in words?
Answer:
Two groups of the sum of five and three

What expression could we write to represent the model?
Answer:
(5 + 3) + (5 + 3) or 2(5 + 3)

Is the model in part (a) equivalent to the model in part (b)?
Answer:
Yes, because both expressions have two 5’s and two 3’s. Therefore, 2 × 5 + 2 × 3 = 2(5 + 3).

d. What relationship do we see happening on either side of the equal sign?
Answer:
On the left-hand side, 2 is being multiplied by 5 and then by 3 before adding the products together. On the right-hand side, the 5 and 3 are added first and then multiplied by 2.

e. In Grade 5 and in Module 2 of this year, you have used similar reasoning to solve problems. What Is the name of the property that is used to say that 2(5 + 3) is the same as 2 × 5 + 2 × 3?
Answer:
The name of the property is the distributive property.

Example 2.
Now we will take a look at an example with variables. Discuss the questions with your partner.

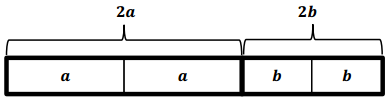
What does the model represent in words?
Answer:
a plus a plus b plus b, two a’s plus two b’s, two times a plus two times b

What does 2a mean?
Answer:
2a means that there are 2 a’s or 2 × a.

How many a’s are in the model?
Answer:
2

How many b’s are in the model?
Answer:
2

What expression could we write to represent the model?
Answer:
2a + 2b

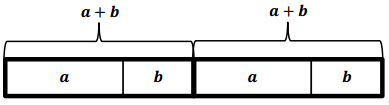
How many a’s are in the expression?
Answer:
2

How many b’s are in the expression?
Answer:
2

What expression could we write to represent the model?
Answer:
(a + b) + (a + b) = 2(a + b)

Are the two expressions equivalent?
Answer:
Yes. Both models include 2 a’s and 2 b’s. Therefore, 2a + 2b = 2(a + b).

Example 3.

Use GCF and the distributive property to write equivalent expressions.
1. 3f + 3g = __________
Answer:
3(f + g)

What is the question asking us to do?
Answer:
We need to rewrite the expression as an equivalent expression in factored form, which means the expression is written as the product of factors. The number outside of the parentheses is the GCF.

How would Problem 1 look if we expanded each term?
Answer:
3 ∙ f + 3 ∙ g

What is the GCF in Problem 1?
Answer:
3

How can we use the GCF to rewrite this expression?
Answer:
3 goes on the outside, and f + g will go inside the parentheses. 3(f + g)

2. 6x + 9y = __________
Answer:
3(2x + 3y)

What is the question asking us to do?
Answer:
We need to rewrite the expression as an equivalent expression in factored form, which means the expression is written as the product of factors. The number outside of the parentheses is the GCF.

How would Problem 2 look if we expanded each term?
Answer:
2 ∙ 3 ∙ x + 3 ∙ 3 ∙ y

What is the GCF in Problem 2?
Answer:
The GCF is 3.

How can we use the GCF to rewrite this expression?
Answer:
I will factor out the 3 from both terms and place it in front of the parentheses. I will place what is left in the terms inside the parentheses: 3(2x + 3y).

3. 3c + 11c = _________
Answer:
c(3 + 11)

Is there a greatest common factor in Problem 3?
Answer:
Yes. When I expand, I can see that each term has a common factor c.
3 ∙ c + 11 ∙ c

Rewrite the expression using the distributive property.
Answer:
c(3 + 11)

4. 24b + 8 = _________
Answer:
8(3b + 1)

Explain how you used GCF and the distributive property to rewrite the expression in Problem 4.
Answer:
I first expanded each term. I know that 8 goes into 24, so I used it in the expansion.
2 ∙ 2 ∙ 2 ∙ 3 ∙ b + 2 ∙ 2 ∙ 2
I determined that 2 ∙ 2 ∙ 2, or 8, is the common factor. So, on the outside of the parentheses I wrote 8, and on the inside I wrote the leftover factor, 3b + 1 ∙ 8(3b + 1)

Why is there a 1 in the parentheses?
Answer:
When I factor out a number, lam leaving behind the other factor that multiplies to make the original number. In this case, when I factor out an 8 from 8, I am left with a 1 because 8 × 1 = 8.

How is this related to the first two examples?
Answer:
In the first two examples, we saw that we could rewrite the expressions by thinking about groups.
We can either think of 24b + 8 as 8 groups of 3b and 8 groups of 1 or as 8 groups of the sum of 3b + 1. This shows that 8(3b) + 8(1) = 8(3b + 1)is the some as 24b + 8.

Eureka Math Grade 6 Module 4 Lesson 11 Exercise Answer Key

Exercise 1.
Apply the distributive property to write equivalent expressions.
a. 7x + 7y
Answer:
7(x + y)

b. 15g + 20h
Answer:
5(3g + 4h)

c. 18m + 42n
Answer:
6(3m + 7n)

d. 30a + 39b
Answer:
3(10a + 13b)

e. 11f + 15f
Answer:
f(11 + 15)

f. 18h + 13h
Answer:
h(18 + 13)

g. 55m + 11
Answer:
11(5m + 1)

h. 7 + 56y
Answer:
7(1 + 8y)

2.
Evaluate each of the expressions below.
a. 6x + 21 y and 3(2x + 7y)                     x = 3 and y = 4
Answer:
6(3) + 21(4)                                             3(23 + 74)
18 + 84                                                    3(6 + 28)
102                                                           3(34)
102                                                           102

b. 5g + 7g and g(5 + 7)                          g = 6
Answer:
5(6) + 7(6)                                              6(5 + 7)
30 + 42                                                   6(12)
72                                                            72

c. 14x + 2 and 2(7x + 1)                          x = 10
Answer:
14(10) + 2                                               2(7.10 + 1)
140 + 2                                                   2(70 + 1)
142                                                          2(71)
142                                                          142

d. Explain any patterns that you notice in the results to parts (a) – c).
Answer:
Both expressions in parts (a) – (c) evaluated to the same number when the indicated value was substituted for the variable. This shows that the two expressions are equivalent for the given values.

e. What would happen if other values were given for the variables?
Answer:
Because the two expressions in each part are equivalent, they evaluate to the same number, no matter what value is chosen for the variable.

Closing

How can use you use your knowledge of GCF and the distributive property to write equivalent expressions?
Answer:
We can use our knowledge of GCF and the distributive property to change expressions from standard form to factored form.

Find the missing value that makes the two expressions equivalent.
4x + 12y                ___(x + 3y)
35x + 50y              ___(7x + 10y)
18x + 9y                ___(2x + y)
32x + 8y                ___(4x + y)
100x + 700y          ___(x + 7y)
Answer:
4x + 12y                 4 (x + 3y)
35x + 50y               5(7x + 10y)
18x + 9y                 9(2x + y)
32x + 8y                 8(4x + y)
100x + 700y           100(x + 7y)

Explain how you determine the missing number.
Answer:
I would expand each term and determine the greatest common factor. The greatest common factor is the number that is placed on the blank line.

Eureka Math Grade 6 Module 4 Lesson 11 Problem Set Answer Key

Question 1.
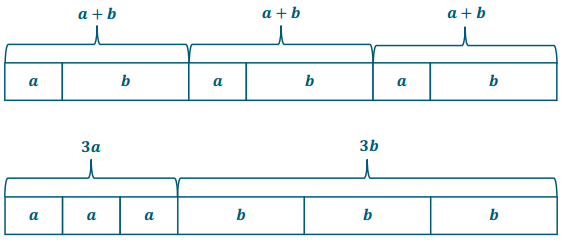
Use models to prove that 3(a + b) is equivalent to 3a + 3b.
Answer:

Question 2.
Use greatest common factor and the distributive property to write equivalent expressions in factored form for the following expressions.
a. 4d + 12e
Answer:
4(d + 3e) or 4(1d + 3e)

b. 18x + 30y
Answer:
6(3x + 5y)

c. 21a + 28y
Answer:
7(3a + 4y)

d. 24f + 56g
Answer:
8(3f + 7g)

Eureka Math Grade 6 Module 4 Lesson 11 Exit Ticket Answer Key

Use greatest common factor and the distributive property to write equivalent expressions in factored form.

Question 1.
2x + 8y
Answer:
2(x + 4y)

Question 2.
13ab + 15 ab
Answer:
ab(13 + 15)

Question 3.
20g + 24h
Answer:
4(5g + 6h)

Eureka Math Grade 6 Module 4 Lesson 11 Greatest Common Factor Answer Key

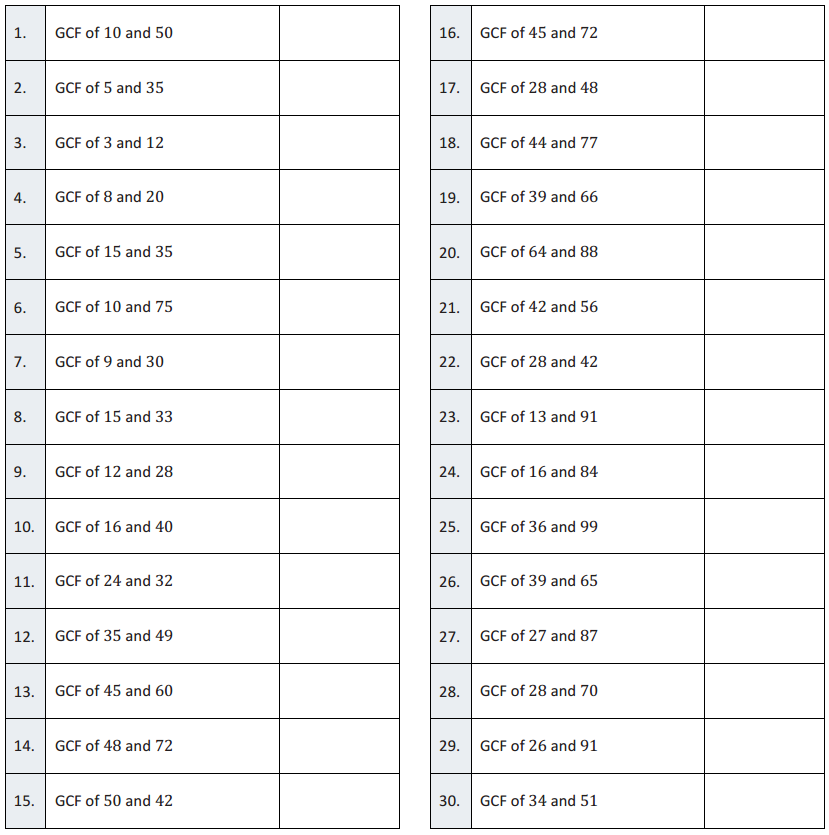
Greatest Common Factor – Round 1
Directions: Determine the greatest common factor of each pair of numbers.

Question 1.
GCF of 10 and 50
Answer:
10

Question 2.
GCF of 5 and 35
Answer:
5

Question 3.
GCF of 3 and 12
Answer:
3

Question 4.
GCF of 8 and 20
Answer:
4

Question 5.
GCF of 15 and 35
Answer:
5

Question 6.
GCF of 10 and 75
Answer:
5

Question 7.
GCF of 9 and 30
Answer:
3

Question 8.
GCF of 15 and 33
Answer:
3

Question 9.
GCF of 12 and 28
Answer:
4

Question 10.
GCF of 16 and 40
Answer:
8

Question 11.
GCF of 24 and 32
Answer:8
Question 12.
GCF of 35 and 49
Answer:
7

Question 13.
GCF of 45 and 60
Answer:
15

Question 14.
GCF of 48 and 72
Answer:
24

Question 15.
GCF of 50 and 42
Answer:
2

Question 16.
GCF of 45 and 72
Answer:
9

Question 17.
GCF of 28 and 48
Answer:
4

Question 18.
GCF of 44 and 77
Answer:
11

Question 19.
GCF of 39 and 66
Answer:
3

Question 20.
GCF of 64 and 88
Answer:
8

Question 21.
GCF of 42 and 56
Answer:
14

Question 22.
GCF of 28 and 42
Answer:
14

Question 23.
GCF of 13 and 91
Answer:
13

Question 24.
GCF of 16 and 84
Answer:
4

Question 25.
GCF of 36 and 99
Answer:
9

Question 26.
GCF of 39 and 65
Answer:
13

Question 27.
GCF of 27 and 87
Answer:
3

Question 28.
GCF of 28 and 70
Answer:
14

Question 29.
GCF of 29 and 91
Answer:
13

Question 30.
GCF of 34 and 51
Answer:
17

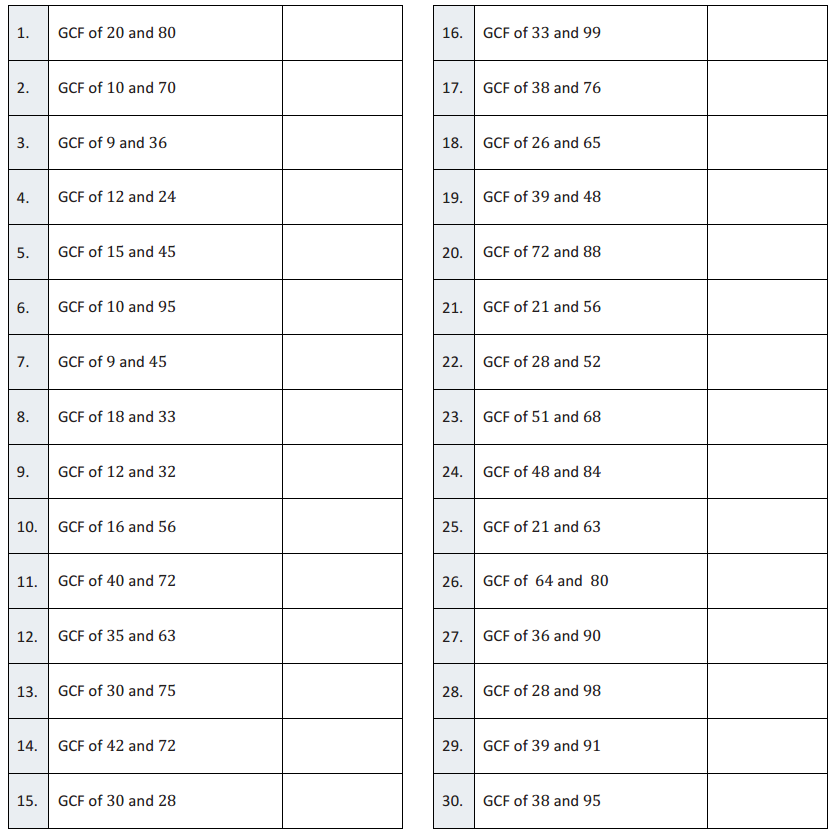
Greatest Common Factor – Round 2
Directions: Determine the greatest common factor of each pair of numbers.

Question 1.
GCF of 20 and 80
Answer:
20

Question 2.
GCF of 10 and 70
Answer:
10

Question 3.
GCF of 9 and 36
Answer:
9

Question 4.
GCF of 12 and 24
Answer:
12

Question 5.
GCF of 15 and 45
Answer:
15

Question 6.
GCF of 10 and 95
Answer:
5

Question 7.
GCF of 9 and 45
Answer:
9

Question 8.
GCF of 18 and 33
Answer:
3

Question 9.
GCF of 12 and 32
Answer:
4

Question 10.
GCF of 16 and 56
Answer:
8

Question 11.
GCF of 40 and 7
Answer:
8

Question 12.
GCF of 35 and 63
Answer:
7

Question 13.
GCF of 30 and 75
Answer:
15

Question 14.
GCF of 42 and 72
Answer:
6

Question 15.
GCF of 30 and 28
Answer:
2

Question 16.
GCF of 33 and 99
Answer:
33

Question 17.
GCF of 38 and 76
Answer:
38

Question 18.
GCF of 26 and 65
Answer:
13

Question 19.
GCF of 39 and 48
Answer:
3

Question 20.
GCF of 72 and 88
Answer:
8

Question 21.
GCF of 21 and 56
Answer:
7

Question 22.
GCF of 28 and 52
Answer:
4

Question 23.
GCF of 51 and 68
Answer:
17

Question 24.
GCF of 48 and 84
Answer:
12

Question 25.
GCF of 21 and 63
Answer:
21

Question 26.
GCF of 64 and 80
Answer:
16

Question 27.
GCF of 36 and 90
Answer:
18

Question 28.
GCF of 28 and 98
Answer:
14

Question 29.
GCF of 39 and 91
Answer:
13

Question 30.
GCF of 38 and 95
Answer:
19