Engage NY Eureka Math 6th Grade Module 3 Lesson 12 Answer Key
Eureka Math Grade 6 Module 3 Lesson 12 Example Answer Key
Example 1: Comparing Order of Integers to the Order of Their Absolute Values
Write an Inequality statement relating the ordered integers from the Opening Exercise. Below each integer, write its absolute value.
Answer:
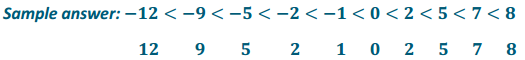
Circle the absolute values that are in increasing numerical order and their corresponding integers. Describe the circled values.
Answer:
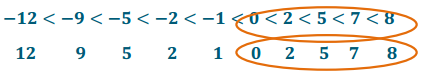
The circled integers are all positive values except zero. The positive integers and their absolute values have the same order.
Rewrite the integers that are not circled in the space below. How do these integers differ from the ones you circled?
Answer:
– 12, – 9, – 5, – 2, – 1
They are all negative integers.
Rewrite the negative integers in ascending order and their absolute values in ascending order below them.
Answer:
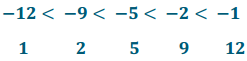
Describe how the order of the absolute values compares to the order of the negative integers.
Answer:
The orders of the negative integers and their corresponding absolute values are opposite.
Example 2: The Order of Negative Integers and Their Absolute Values
Draw arrows starting at the dashed line (zero) to represent each of the integers shown on the number line below. The arrows that correspond with 1 and 2 have been modeled for you.
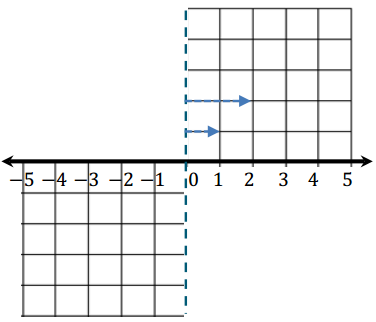
Answer:
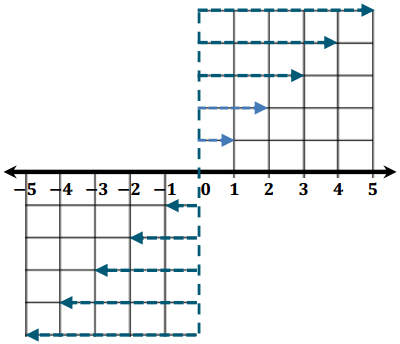
As you approach zero from the left on the number line, the integers ___________, but the absolute values of those integers ___________. This means that the order of negative integers is ___________ the order of their absolute values.
Answer:
As you approach zero from the left on the number line, the integers increase , but the absolute values of those integers decrease . This means that the order of negative integers is opposite the order of their absolute values.
Eureka Math Grade 6 Module 3 Lesson 12 Exercise Answer Key
Complete the steps below to order these numbers:
{2.1, – 4\(\frac{1}{2}\), – 6. 0.25, – 1.5, 0, 3.9, – 6.3, – 4, 2\(\frac{3}{4}\), 3.99, – 9\(\frac{1}{4}\)}
a. Separate the set of numbers into positive rational numbers, negative rational numbers, and zero in the top cells below (order does not matter).
Answer:
b. Write the absolute values of the rational numbers (order does not matter) in the bottom cells below.
Answer:
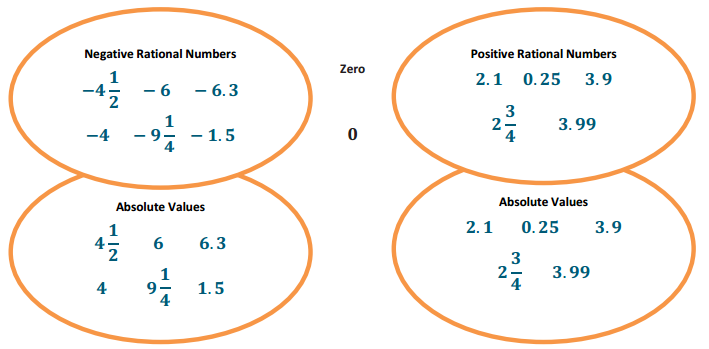
c. Order each subset of absolute values from least to greatest.

Answer:
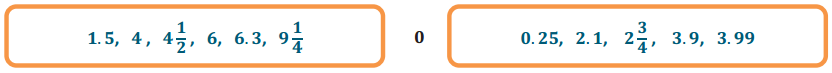
d. Order each subset of rational numbers from least to greatest.

Answer:

e. Order the whole given set of rational numbers from least to greatest.
Answer:
– 9\(\frac{1}{4,}\), – 6.3, – 6, – 4\(\frac{1}{2}\), – 4, – 1.5, 0, 0.25, 2.1, 2\(\frac{3}{4}\), 3.9, 3.99
Exercise 2.
a. Find a set of four integers such that their order and the order of their absolute values are the same.
Answer:
Answers will vary. An example follows: 4, 6, 8, 10
b. Find a set of four integers such that their order and the order of their absolute values are opposite.
Answer:
Answers will vary. An example follows: – 10, – 8, – 6, – 4
c. Find a set of four non-integer rational numbers such that their order and the order of their absolute values are the same.
Answer:
Answers will vary. An example follows: 2\(\frac{1}{2}\), 3\(\frac{1}{2}\), 4\(\frac{1}{2}\), 5\(\frac{1}{2}\)
d. Find a set of four non-integer rational numbers such that their order and the order of their absolute values are opposite.
Answer:
Answers will vary. An example follows: – 5\(\frac{1}{2}\), – 4\(\frac{1}{2}\), – 3\(\frac{1}{2}\), – 2\(\frac{1}{2}\)
e. Order all of your numbers from parts (a) – (d) in the space below. This means you should be ordering 16 numbers from least to greatest.
Answer:
Answers will vary. An example follows:
– 10, – 8, – 6, – 5\(\frac{1}{2}\), – 4\(\frac{1}{2}\), – 4, – 3\(\frac{1}{2}\), – 2\(\frac{1}{2}\), 2\(\frac{1}{2}\), 3\(\frac{1}{2}\), 4, 4\(\frac{1}{2}\), 5\(\frac{1}{2}\), 6, 8, 10
Eureka Math Grade 6 Module 3 Lesson 12 Problem Set Answer Key
Question 1.
Micah and Joel each have a set of five rational numbers. Although their sets are not the same, their sets of numbers have absolute values that are the same. Show an example of what Micah and Joel could have for numbers. Give the sets in order and the absolute values in order.
Answer:
Examples may vary, If Micah had 1, 2, 3, 4, 5, then his order of absolute values would be the same: 1, 2, 3, 4, 5. If Joel had the numbers – 5, – 4, – 3, -2, -1, then his order of absolute values would also be 1, 2, 3, 4, 5.
Enrichment Extension: Show an example where Micah and Joel both have positive and negative numbers.
Answer:
If Micah had the numbers: – 5, – 3, – 1, 2, 4, his order of absolute values would be 1, 2, 3, 4, 5. If Joel hod the numbers – 4, – 2, 1, 3, 5, then the order of his absolute values would also be 1, 2, 3, 4, 5.
Question 2.
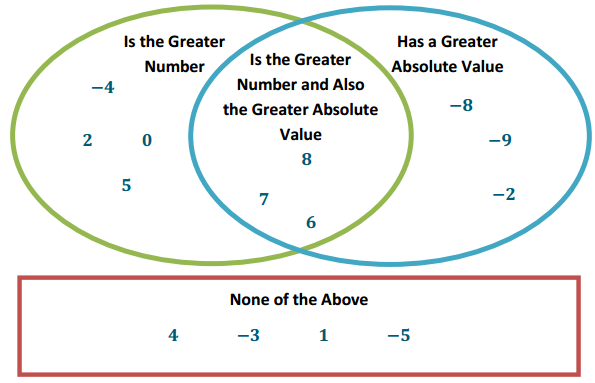
For each pair of rational numbers below, place each number In the Venn diagram based on how it compares to the other.
a. – 4, – 8
b. 4,8
C. 7,- 3
d. – 9,2
e. 6,1
f. – 5,5
g. – 2,0
Answer:
Eureka Math Grade 6 Module 3 Lesson 12 Exit Ticket Answer Key
Question 1.
Bethany writes a set of rational numbers in increasing order. Her teacher asks her to write the absolute values of these numbers in Increasing order. When her teacher checks Bethany’s work, she Is pleased to see that Bethany has not changed the order of her numbers. Why is this?
Answer:
All of Bethany’s rational numbers are positive or 0. The positive rational numbers have the same order as their absolute values. If any of Bethany’s rational numbers are negative, then the order would be different.
Question 2.
Mason was ordering the following rational numbers In math class: – 3. 3, – 15, – 8\(\frac{8}{9}\).
a. Order the numbers from least to greatest.
Answer:
– 15, – 8\(\frac{8}{9}\), – 3.3
b. List the order of their absolute values from least to greatest.
Answer:
3.3, 8\(\frac{8}{9}\), 15
c. Explain why the orderings in parts (a) and (b) are different.
Answer:
Since these are all negative numbers, when I ordered them from least to greatest, the one farthest away from zero (farthest to the left on the number line) came first. This number is – 15. Absolute value is the numbers’ distance from zero, and so the number farthest away from zero has the greatest absolute value, so 15 will be greatest in the list of absolute values, and so on.
Eureka Math Grade 6 Module 3 Lesson 12 Opening Exercise Answer Key
Record your integer values in order from least to greatest in the space below.
Answer:
Sample answer: – 12, – 9, – 5, – 2, – 1, 0, 2, 5, 7, 8