Engage NY Eureka Math 6th Grade Module 2 Lesson 2 Answer Key
Eureka Math Grade 6 Module 2 Lesson 2 Example Answer Key
Example 1.
Question # _________
Write It as a division expression. ______________
Write It as a multiplication expression. ______________
Make a rough draft of a model to represent the problem:
As you travel to each model, be sure to answer the following questions:
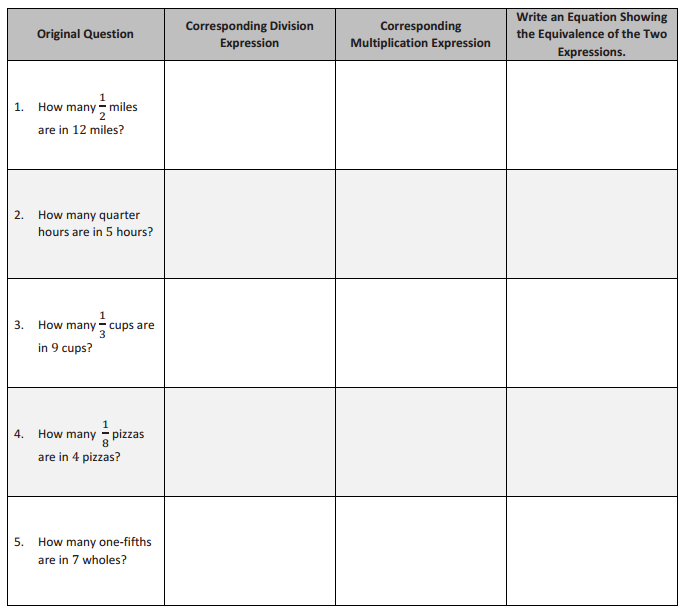
Answer:
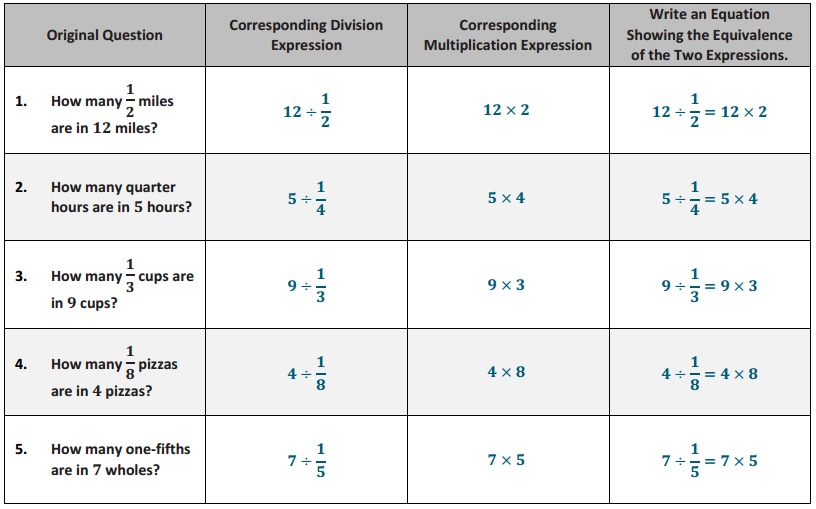
Example 2.
Molly has 9 cups of flour. If this is \(\frac{3}{4}\) of the amount she needs to make bread, how many cups does she need?
a. Construct the tape diagram by reading it backward. Draw a tape diagram and label the unknown.
Answer:

b. Next, shade in \(\frac{3}{4}\).
Answer:

c. Label the shaded region to show that 9 is equal to \(\frac{3}{4}\) of the total.
Answer:
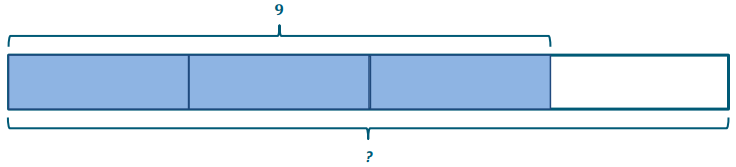
d. Analyze the model to determine the quotient.
Answer:
3 units = 9
1 unit = 9 ÷ 3 = 3
4units = 4 × 3 = 12
Molly needs 12 cups of flour to make bread.
Eureka Math Grade 6 Module 2 Lesson 2 Exercise Answer Key
Exercise 1.
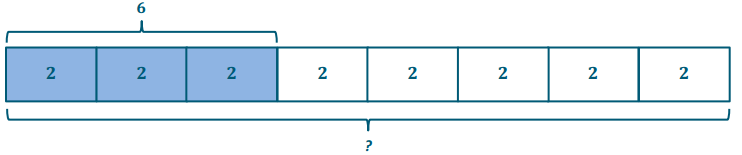
A construction company is setting up signs on 2 miles of a road. If the company places a sign at every mile, how many signs will it use?
Answer:
2 ÷ \(\frac{1}{4}\) → Haw many \(\frac{1}{4}\) in 2?
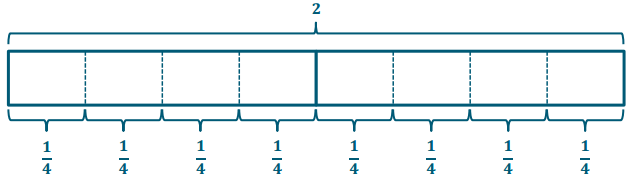
2 ÷ \(\frac{1}{4}\) = 8 fourths ÷ 1 fourth = 8
There are 8 fourths in 2. The company will use 8 signs.
Exercise 2.
George bought 4 submarine sandwiches for a birthday party. If each person will eat \(\frac{2}{3}\) of a sandwich, how many people can George feed?
Answer:
4 ÷ \(\frac{2}{3}\) → Haw many \(\frac{2}{3}\) in 2?
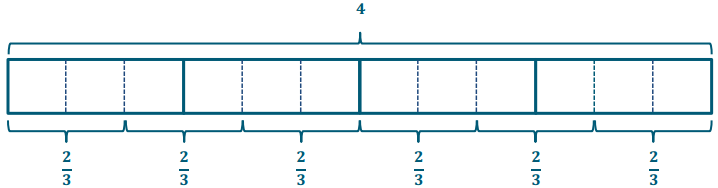
4 ÷ \(\frac{2}{3}\) = 12 thirds ÷ 2 thirds = 8
There are 6 two-thirds in 4. George can feed 6 people.
Exercise 3.
Miranda buys 6 pounds of nuts. If she puts \(\frac{3}{4}\) pound In each bag, how many bags can she make?
Answer:
6 ÷ \(\frac{3}{4}\) → Haw many \(\frac{3}{4}\) in 6?
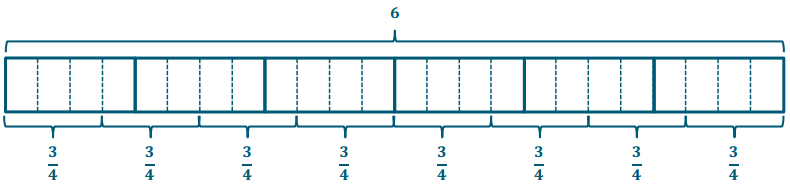
6 ÷ \(\frac{3}{4}\) = 24 fourths ÷ 3 fourths = 8
There are 8 three-fourths in 6. Miranda can make 8 bags.
Exercise 4.
Margo freezes 8 cups of strawberries. If this is \(\frac{2}{3}\) of the total strawberries that she picked, how many cups of strawberries did Margo pick?
Answer:
8 ÷ \(\frac{2}{3}\) → 8 is \(\frac{2}{3}\) group of what size?
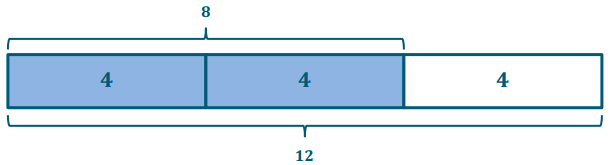
2 units = 8
1 unit = 8 ÷ 2 = 4
3 units = 3 × 4 = 12
Margo picked 12 cups of strawberries.
Exercise 5.
Regina is chopping up wood. She has chopped 10 logs so far. If the 10 logs represent \(\frac{5}{8}\) of all the logs that need to be chopped, how many logs need to be chopped in all?
Answer:
10 ÷ \(\frac{5}{8}\) → 10 is 6 ÷ \(\frac{5}{8}\) group of what size?
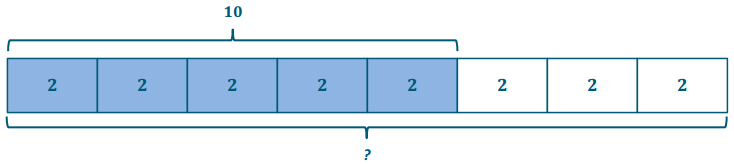
5 units = 10
1 unit = 10 ÷ 5 = 2
B units = 8 × 2 = 16
Regina will chop 16 logs.
Eureka Math Grade 6 Module 2 Lesson 2 Problem Set Answer Key
Rewrite each problem as a multiplication question. Model your answer.
Question 1.
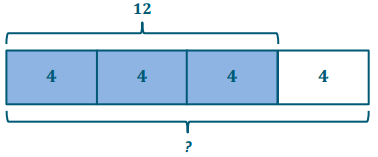
Nicole used \(\frac{3}{8}\) of her ribbon to wrap a present. If she used 6 feet of ribbon for the present, how much ribbon did Nicole have at first?
Answer:
6 ÷ \(\frac{3}{8}\)
6 is \(\frac{3}{8}\) of what number?
3 units = 6
1 unit = 6 ÷ 3 = 2
8 units = 8 × 2 = 16
Nicole started with 16 feet of ribbon.
Question 2.
A Boy Scout has 3 meters of rope. He cuts the rope into cords \(\frac{3}{5}\)m long. How many cords will he make?
Answer:
How many \(\frac{3}{5}\) are in 3?
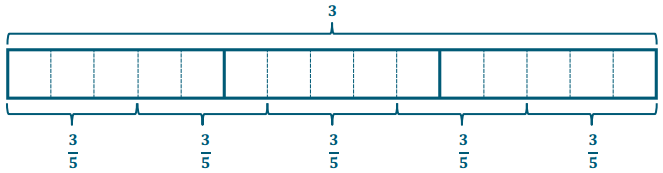
3 ÷ \(\frac{3}{5}\) = 15 fifths ÷ 3 fifths = \(\frac{15}{3}\) = 5
The Boy Scout can make 5 cords.
Question 3.
12 gallons of water fill a tank to \(\frac{3}{4}\) capacity.
a. What is the capacity of the tank?
Answer:
12 ÷ \(\frac{3}{4}\)
12 is \(\frac{3}{4}\) of what number?
3units = 12
1 unit = 12 ÷ 3 = 4
4 units = 4 × 4 = 16
The tank’s capacity is 16 gallons.
b. If the tank is then filled to capacity, how many half-gallon bottles can be filled with the water in the tank?
Answer:
How many \(\frac{1}{2}\) are in 16?
16 ÷ \(\frac{1}{2}\) = 32 halves ÷ 1 half = 32
32 bottles can be filled.
Question 4.
Hunter spent \(\frac{2}{3}\) of his money on a video game before spending half of his remaining money on lunch. If his lunch costs $10, how much money did he have at first?
Answer:
$10 is \(\frac{1}{6}\) of what number?
10 ÷ \(\frac{1}{6}\)
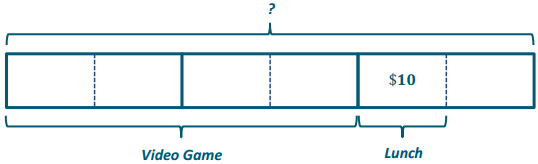
1 unit = $ 10
6 units = 6 × $10 = $60
Hunter had $60 at first.
Question 5.
Students were surveyed about their favorite colors. \(\frac{1}{4}\) of the students preferred red, \(\frac{1}{8}\) of the students preferred blue, and of the remaining students preferred green. If 15 students preferred green, how many students were surveyed?
Answer:
15 is \(\frac{3}{8}\) of what number?
15 ÷ \(\frac{3}{8}\)
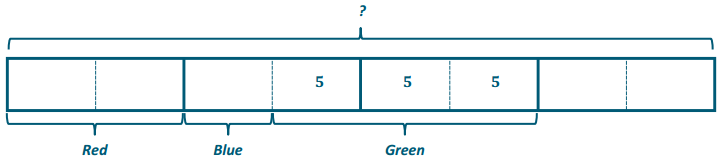
3 units = 15
1 unit = 15 ÷ 3 = 5
8 units = 8 × 5 = 40
40 students were surveyed.
Question 6.
Mr. Scruggs got some money for his birthday. He spent \(\frac{1}{5}\) of it on dog treats. Then, he divided the remainder equally among his 3 favorite charities.
a. What fraction of his money did each charity receive?
Answer:
\(\frac{4}{5} \div 3=\frac{1}{3} \times \frac{4}{5}=\frac{4}{15}\) Each charity received \(\frac{4}{15}\) of Mr. Scruggs’ birthday money.
b. If he donated $60 to each charity, how much money did he receive for his birthday?
Answer:
60 is \(\frac{4}{15}\) of what number?
60 ÷ \(\frac{4}{15}\)
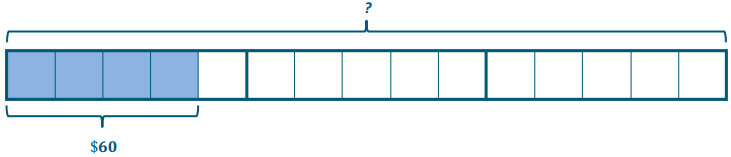
4 units = $60
1 unit = $60 ÷ 4 = $15
15 units = 15 × $15 = $225
Mr. Scruggs got $225 for his birthday.
Eureka Math Grade 6 Module 2 Lesson 2 Exit Ticket Answer Key
Solve each division problem using a model.
Question 1.
Henry bought 4 pies, which he plans to share with a group of his friends. If there Is exactly enough to give each member of the group one-sixth of the pie, how many people are In the group?
Answer:
4 ÷ \(\frac{1}{6}\) → How many \(\frac{1}{6}\) in 4?
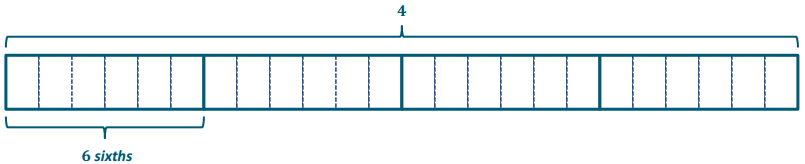
There are 6 sixths in 1, and 24 sixths in 4. Henry can share the pies with 24 people.
Question 2.
Rachel finished \(\frac{3}{4}\) of the race in 6 hours. How long was the entire race?
Answer:
6 ÷ \(\frac{3}{4}\) → \(\frac{3}{4}\) of what number is 6?
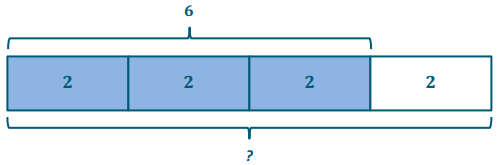
3 units = 6
1 units = 6 ÷ 3 = 2
4 units = 4 × 2 = 8
The race was 8 hours.