Engage NY Eureka Math 6th Grade Module 2 End of Module Assessment Answer Key
Eureka Math Grade 6 Module 2 End of Module Assessment Answer Key
Question 1.
LB. Johnson Middle School held a track and field event during the school year. The chess club sold various drink and snack items for the participants and the audience. Altogether, they sold 486 items that totaled $2,673.
a. If the chess club sold each item for the same price, calculate the price of each item.
Answer:
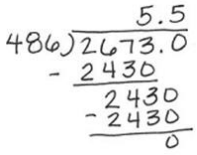
Each item’s price is $5.50
b. Explain the value of each digit in your answer to 1(a) using place value terms.
Answer:
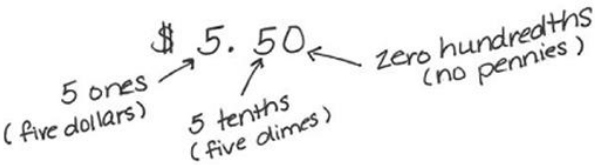
Question 2.
The long-jump pit was recently rebuilt to make it level with the runway. Volunteers provided pieces of
wood to frame the pit. Each piece of wood provided measures 6 feet, which is approximately 1.8287
meters.

a. Determine the amount of wood, in meters, needed to rebuild the frame.
Answer:

b. How many boards did the volunteers supply? Round your calculations to the nearest hundredth, and then provide the whole number of boards supplied.
Answer:

Question 3.
Andy runs 436.8 meters in 62.08 seconds.
a. If Andy runs at a constant speed, how far does he run in one second? Give your answer to the nearest tenth of a second.
Answer:

b. Use place value, multiplication with powers of 10, or equivalent fractions to explain what is happening mathematically to the decimal points in the divisor and dividend before dividing.
Answer:
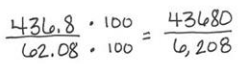
When you write the problem as a fraction, multiply the numerator and denominator by 100. Multiplying each by 100 resulted in both numbers being whole numbers.
436.8 ÷ 62.08 is the same as 43,680 ÷ 6,208.
c. In the following expression, place a decimal point in the divisor and the dividend to create a new problem with the same answer as in 3(a). Then, explain how you know the answer will be the same.
43.68 ÷ 6.208
Answer:
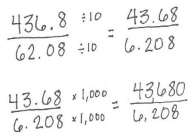
Multiplying or dividing the dividend and divisor by the same power of ten yields the same quotient.
Question 4.
The PTA created a cross-country trail for the meet.
a. The PTA placed a trail marker in the ground every four hundred yards. Every nine hundred yards, the PTA set up a water station. What is the shortest distance a runner will have to run to see both a water station and trail marker at the same location?
Answer:
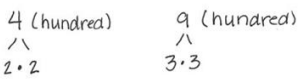
LCM 2 . 2 . 3 . 3 = 36 hundred
36 hundred yards
b. There are 1,760 yards in one mile. About how many miles will a runner have to run before seeing both a water station and trail marker at the same location? Calculate the answer to the nearest hundredth of a mile.
Answer:
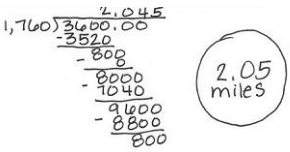
c. The PTA wants to cover the wet areas of the trail with wood chips. They find that one bag of wood
chips covers a 3\(\frac{1}{2}\)-yard section of the trail. If there is a wet section of the trail that is approximately 50\(\frac{1}{4}\) yards long, how many bags of wood chips are needed to cover the wet section of the trail?
Answer:

Question 5.
The Art Club wants to paint a rectangle-shaped mural to celebrate the winners of the track and field meet. They design a checkerboard background for the mural where they will write the winners’ names. The rectangle measures 432 inches in length and 360 inches in width. Apply Euclid’s algorithm to determine the side length of the largest square they can use to fill the checkerboard pattern completely without overlap or gaps.
Answer:
