Eureka Math Grade 5 Module 5 Lesson 15 Answer Key

Engage NY Eureka Math 5th Grade Module 5 Lesson 15 Answer Key

Eureka Math Grade 5 Module 5 Lesson 15 Problem Set Answer Key

Question 1.
The length of a flowerbed is 4 times as long as its width. If the width is “\(\frac{3}{8}\) meter, what is the area?
Answer:

Given,

The width of the flower bed = 3/8 meters

The length of the flower bed is 4 times as long as its width

Which means, 3/8 x 4 = 12/ 8 = 3/2

Now, Area = length x width

A= 3/2 x 3/8

A = 9/16

Therefore, the area of the flowerbed is 9/16 m².

Question 2.
Mrs. Johnson grows herbs in square plots. Her basil plot measures \(\frac{5}{8}\) yd on each side.
a. Find the total area of the basil plot.

b. Mrs. Johnson puts a fence around the basil. If the fence is 2 ft from the edge of the garden on each side, what is the perimeter of the fence in feet?
c. What is the total area, in square feet, that the fence encloses?
Answer:

a.

Given,

The measurement of basil plot on each side = 5/9 yard

Now, Area = length x width

A= 5/8 x 5/8 = 25/64

Therefore, the area of the basil plot = 25/64 yd²

b.

The measurement of basil plot in each side = 5/9 yard

= 5/8 x 3

=  15/8 or 1 7/8 feet

Now, the length of one side

2 feet + 2 feet + 1 7/8 feet

= 5 7/8

Perimetre = 4 x sides

= 4 x 5 7/8

= 20 + 3 4/8

= 23 1/2

Therefore, the perimetre of the fence = 23 1/2 feet.

c.

The total area that the fence encloses

= length x width

= 5 7/8 x 5 7/8

=  ( 5 x 5 ) + ( 5 x 7/8 ) +( 5 x 7/8 ) + ( 7/8 x 7/8 )

= 25 + 4 3/8 + 4 3/8 + 49/64

= 33 + 48/64 + 49/64

= 33 + 97/64

= 34 33/64

Therefore, the area that fence encloses = 34 33/64 square feet.

Question 3.
Janet bought 5 yards of fabric 2\(\frac{1}{4}\)-feet wide to make curtains. She used \(\frac{1}{3}\) of the fabric to make a long set of curtains and the rest to make 4 short sets.
a. Find the area of the fabric she used for the long set of curtains.
b. Find the area of the fabric she used for each of the short sets.
Answer:

a.

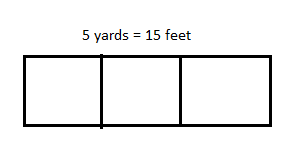
Area = length x width

= 5 x 2 1/4

= 10 + 5/4

= 11 1/4 square feet

Therefore, the area of long set is 11 1/4 square feet

b.

15 feet – 5 feet = 10 feet

1/4 of 10 is 2 1/2 feet

Now, the area of each set of shorter curtain

A = 2 1/2 x 2 1/2

( 2 x 2 ) + ( 2 x 1/2 ) + ( 2 x 1/2 ) + ( 1/2 x 1/2 )

= 4 + 1/2 + 1 + 1/8

= 5 + 1/2 +1/8

= 5 5/8 square feet

Therefore, the area of each set of shorter curtain is 5 5/8 square feet.

 

Question 4.
Some wire is used to make 3 rectangles: A, B, and C. Rectangle bs dimensions are \(\frac{3}{5}\) cm larger than Rectangle A’s dimensions, and Rectangle C’s dimensions are \(\frac{3}{5}\) cm larger than Rectangle B’s dimensions. Rectangle A is 2 cm by 3\(\frac{1}{5}\) cm.
a. What is the total area of all three rectangles?
b. If a 40-cm coil of wire was used to form the rectangles, how much wire is left?
Answer:

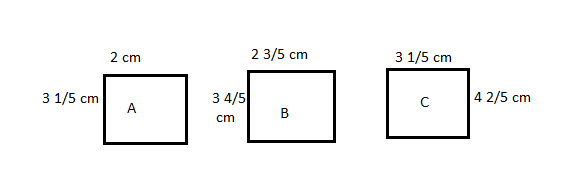
a.

The area of rectangle A =

Area = length x width

A = 2 X 3 1/5

=  6 + 2/5

= 6 2/5 square centimetres

Area of of rectangle B =

A = 2 3/5 cm x 3 4/5 cm

= 6 + 8/5 + 9/5 + 12/25

= 9 + 21/5 + 12/25

= 9 22/25 square centimetres

Area of rectangle C =

A =  3 1/5 cm x 4 2/5 cm

= 12 + 6/5 + 4/5 + 2/25

= 14 2/25 square centimetres

Total area of three rectangles =

= 6 2/5 + 9 22/25 + 14 2/25

= 29 + 2/5 + 24/25

= 29 +10/25 +24/25

= 30 9/25 square centimetres

Therefore, the area of three rectangles = 30 9/25 square centimetres.

b.

Perimeter of rectangle A =

2 + 2 + 3 1/5 + 3 1/5

= 6 2/5  centimetres

Perimeter of rectangle B =

2 3/5 + 2 3/5 + 3 4/5 + 3 4/5

= 12 4/5 centimetres

Perimeter of rectangle C =

3 1/5 + 3 1/5 + 4 2/5 + 4 2/5

= 15 1/5 centimetres

Total perimeter =

1 2/5 cm + 12 4/5 cm + 15 1/5 cm

= 38 2/5 cm

Now, according to the given condition :

40 cm – 38 2/5 cm

= 1 3/5 cm

Therefore, the leftover wire length = 1 3/5 cm.

Eureka Math Grade 5 Module 5 Lesson 15 Exit Ticket Answer Key

Wheat grass is grown in planters that are 3\(\frac{1}{2}\) inch by 1\(\frac{3}{4}\) inch. If there is a 6 × 6 array of these planters with no space between them, what is the area covered by the planters?
Answer:

The area of planter =

3 1/2 x 1 3/4

( 3 x  1 ) + ( 3 x 3/4 ) + ( 1 x 1/2 ) + ( 1/2 x 3/4 )

= 3 + 9/4 + 1/2 + 3/8

= 24 + 18/8 + 4/8 + 3/8

=49/8 = 6 1/8

According to given condition

6 x 6 = 36

= 36 x  6 1/8

216 9/8

= 200 + 1/2

= 200 1/2

Therefore, the area covered by the planters = 200 1/2 square inches.

Eureka Math Grade 5 Module 5 Lesson 15 Homework Answer Key

Question 1.
The width of a picnic table is 3 times its length. If the length is \(\frac{5}{6}\)-yd long, what is the area of the picnic table in square feet?
Answer:

1 yard = 3 feet

The area of the picnic table =

5/6 x 3= 15/6 = 5/2 = 2 1/2 feet

Area = 2 1/2 x 7 1/2

A = 5/2 x 15 1/2

= 75/4

= 18 3/4  square feet

Therefore, the area of the table = 2 1/2 square yards.

Question 2.
A painting company will paint this wall of a building. The owner gives them the following dimensions:

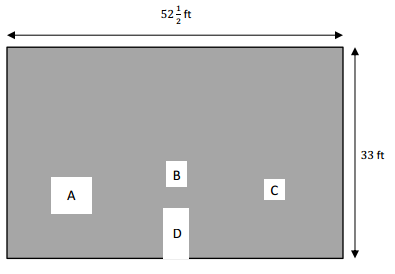
Window A is 6\(\frac{1}{4}\) ft × 5\(\frac{3}{4}\) ft.
Window B is 3\(\frac{1}{8}\) ft × 4 ft.
Window C is 9\(\frac{1}{2}\) ft².
Door D is 4 ft × 8 ft.
What is the area of the painted part of the wall?
Answer:

The area of window A =

= 6 1/4 x  5 3/4

= 30 x  1 1/4 + 4 2/4 + 3/16

= 35 + 3/4 + 3/16

= 35 + 15/16

= 35 15/16 square feet

The area of window B =

3 1/8 x 4

= 12 + 4/8

= 12 1/2 square feet

The area of D  =

4 x 8 = 32 square feet

The total area of the wall =

52 1/2 x 33

= 1716 + 33/2

= 1732 1/2 square feet

Now, the total area of A,B,C A and D

= 35 15/16 +12 1/2 + 32 + 9 1/2

= 22 + 35 15/16 +32

= 89 15/16

Now, the area of the painted wall =

1732 1/2 sq. ft – 89 15/16

= 1642 9/16 square feet

Therefor, the area of the wall painted = 1642 9/16 square feet.

Question 3.
A decorative wooden piece is made up of four rectangles as shown to the right. The smallest rectangle measures 4\(\frac{1}{2}\) inches by 7\(\frac{3}{4}\) inches. If 2\(\frac{1}{4}\) inches are added to each dimension as the rectangles get larger, what is the total area of the entire piece?

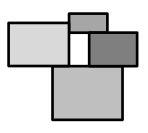
Answer:

The area of the smallest rectangle =

4 1/2 x 7 3/4

= 24 + 3 + 3 1/2 + 3/8

= 34 7/8 square inches

b. Now,

4 1/2 + 2 1/4

= 4 2/4 + 2 1/4

= 6 3/4

7 3/4 + 2 1/4 = 10

36 3/4 x 10

= 60 + 7 2/4

= 67 1/2 square inches

c.

6 3/4 + 2 1/4 =9

10 + 2 1/4

= 12 1/4

9 x 12 1/4 =

= 108 + 2 1/4 = 110 1/4 square inches

D.

d. 9 + 2 1/4 = 11 1/4

12 1/4 + 2 1/4 = 14 2/4

11 1/4 x 14 2/4

= 154 + 3 2/4 + 5 1/2 + 1/8

= 163 1/8 square inches.

So, the total area of the figure = 110 + 34 + 67 + 163

= 374 + 1 3/4

= 375 3/4 square inches