Eureka Math Grade 4 Module 6 End of Module Assessment Answer Key

Engage NY Eureka Math 4th Grade Module 6 End of Module Assessment Answer Key

Eureka Math Grade 4 Module 6 End of Module Assessment Task Answer Key

Question 1.
Decompose each fraction into hundredths using area models. Then, write the equivalent number sentence using decimals.
a. \(\frac{8}{10}\) = 0.8

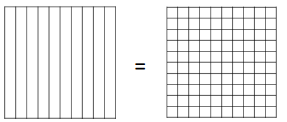
Answer:
8/10 = 0.8.

Explanation:
In the above-given question,
given that,
\(\frac{8}{10}\).
8/10 = 0.8.

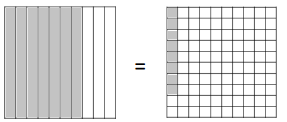
b. \(\frac{18}{10}\) = 1.8

Answer:
18/10 = 1.8.

Explanation:
In the above-given question,
given that,
\(\frac{18}{10}\).
18/10 = 1.8.

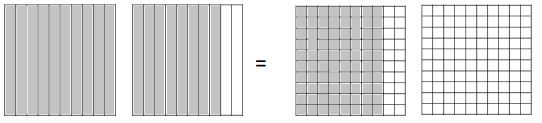
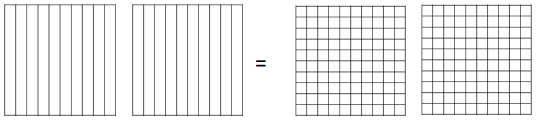
Decompose each fraction into hundredths. Then, write the equivalent number sentence for each part using decimals.
c. \(\frac{2}{10}\) = 0.2
d. \(\frac{5}{10}\) = 0.5

Answer:
2/10 = 0.2.

Explanation:
In the above-given question,
given that,
\(\frac{2}{10}\).
2/10 = 0.2.

Answer:
5/10 = 0.5.

Explanation:
In the above-given question,
given that,
\(\frac{5}{10}\).
5/10 = 0.5.

Question 2.
Several points are plotted on the number lines below. Identify the decimal number associated with each point.

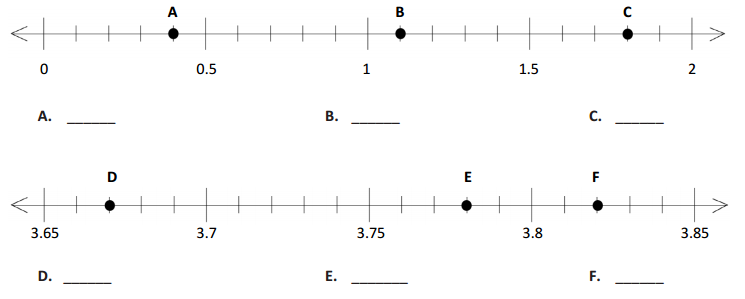
Answer:
0.4

Explanation:
In the above-given question,
given that,
\(\frac{5}{10}\).
5/10 = 0.5.

Answer:
1.1

Explanation:
In the above-given question,
given that,
\(\frac{11}{10}\).
11/10 = 1.1.

Answer:
1.8

Explanation:
In the above-given question,
given that,
\(\frac{18}{10}\).
18/10 = 1.8.

Answer:
3.67

Explanation:
In the above-given question,
given that,
\(\frac{365}{100}\).
365/100 = 3.67.

Answer:
3.78

Explanation:
In the above-given question,
given that,
\(\frac{378}{100}\).
378/100 = 3.75.

Answer:
3.82

Explanation:
In the above-given question,
given that,
\(\frac{382}{100}\).
382/100 = 3.82.

Question 3.
Use the symbols >, =, or < to compare the following. Justify your conclusions using pictures, numbers, or words.
a. a. 0.02 < 0.22
b. 0.6 = 0.60
c. 17 tenths = 1.7
d. 1.04 > 1\(\frac{4}{10}\)
e. 0.38 > \(\frac{38}{10}\)
f. 4.05 = 4\(\frac{5}{100}\)
g. 3 tenths + 2 hundredths > 1 tenth + 13 hundredths
h. 8 hundredths + 7 tenths > 6 tenths + 17 hundredths

Answer:
0.02 < 0.22.
0.6 = 0.60.
17 tenths = 1.7
1.04 > 1.4
0.38 > 3.8
4.05 = 4.05
3 tenths + 2 hundredths > 1 tenth + 13 hundredths.
8 hundredths + 7 tenths > 6 tenths + 17 hundredths.

Explanation:
In the above-given question,
given that,
0.02 < 0.22.
0.6 = 0.60.
17 tenths = 1.7
17/10 = 1.7
1.04 > 1.4
0.38 > 3.8
4.05 = 4.05
3 tenths + 2 hundredths > 1 tenth + 13 hundredths.
3/10 + 2/100 = 0.3 + 0.02 = 0.32.
1/10 + 13/100 = 0.1 + 0.13 = 0.23.
8 hundredths + 7 tenths > 6 tenths + 17 hundredths.
8/100 + 7/10 = 0.7 + 0.08 = 0.78.
6/10 + 17/100 = 0.6 + 0.17 = 0.77.

Question 4.
Solve.
a. Express your solution as a fraction of a meter. 0.3 m + 1.45 m
b. Express your solution as a fraction of a liter. 1.7 L + 0.82 L
c. Express your solution as a fraction of a dollar. 4 dimes 1 penny + 77 pennies

Answer:
3/10 + 145/100.
17/10 + 82/100.
41/10 + 77/100.

Explanation:
In the above-given question,
given that,
0.3 m + 1.45 m.
3/10 + 145/100.
17/10 = 1.7.
82/100 = 0.82.
41/10 = 4.1.
77/100 = 0.77.

Question 5.
Solve.
a. \(\frac{7}{10}+\frac{8}{100}\)
b. \(\frac{4}{10}+\frac{51}{100}\)
c. \(\frac{5}{10}+\frac{68}{100}\)
d. \(\frac{98}{100}+\frac{2}{10}\)
e. \(\frac{12}{100}+\frac{12}{10}\)
f. \(\frac{1}{10}+\frac{13}{100}+\frac{8}{10}\)

Answer:
7/10 + 8/100 = 0.78.
4/10 + 51/100 = 0.91.
5/10 + 68/100 = 1.18.
2/10 + 98/100 = 1.18.
12/10 + 12/100 = 1.32.
1/10 + 8/10 + 13/100 = 1.13.

Explanation:
In the above-given question,
given that,
7/10 + 8/100 = 0.78.
4/10 + 51/100 = 0.91.
5/10 + 68/100 = 1.18.
2/10 + 98/100 = 1.18.
12/10 + 12/100 = 1.32.
1/10 + 8/10 + 13/100 = 1.13.

Question 6.
Answer the following questions about a track meet.
a. Jim and Joe ran in a relay race. Jim had a time of 9.8 seconds. Joe had a time of 10.32 seconds. Together, how long did it take them to complete the race? Record your answer as a decimal.

Answer:
The long did it take them to complete the race = 21.12 seconds.

Explanation:
In the above-given question,
given that,
Jim and role ran in a relay race.
Jim had a time of 9.8 seconds.
Joe had a time of 10.32 seconds.
9.8 + 10.32 = 21.12 seconds.

b. The times of the 5 fastest runners were 7.11 seconds, 7.06 seconds, 7.6 seconds, 7.90 seconds, and 7.75 seconds. Locate these times on the number line. Record the times as decimals and fractions. One has been completed for you.

Answer:
7.11, 7.06, 7.6, 7.90, 7.75.

Explanation:
In the above-given question,
given that,
7.11 = 7 x 11/100.
7.06 = 7 x 6/100.
7.6 = 7 x 6/10.
7.90 = 7 x 9/100.
7.75 = 7 x 75/100.

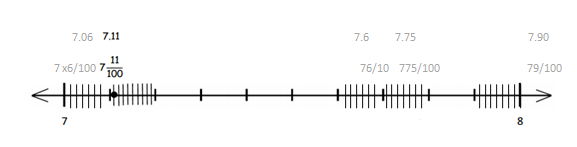
c. Natalie threw a discus 32.04 meters. She threw 3.8 meters farther on her next throw. Write a statement to compare the two distances that Natalie threw the discus using >, <, or =.

Answer:
32.04 > 3.8.

Explanation:
In the above-given question,
given that,
Natalie threw a discus 32.04 meters.
she threw 3.8 meters farther on her next throw.
32.04 is greater than 3.8.

d. At the concession stand, Marta spent 89 cents on a bottle of water and 5 dimes on a bag of chips. Shade the area models to represent the cost of each item.

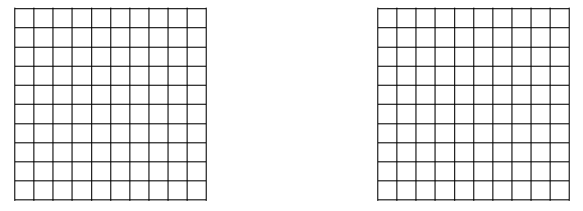
Answer:
89 cents.
5 dimes.

Explanation:
In the above-given question,
given that,
89 cents.
5 dimes.

e. Write a number sentence in fraction form to find the total cost of a water bottle and a bag of chips. After solving, write the complete number sentence in decimal form.

Answer:
89 cents = 0.89.
5 dimes = 0.05.

Explanation:
In the above-given question,
given that,
89 cents.
5 dimes.

f. Brian and Sonya each have a container. They mark their containers to show tenths. Brian and Sonya both fill their containers with 0.7 units of juice. However, Brian has more juice in his container. Explain how this is possible.

Answer:
The brain has more juice in its container.

Explanation:
In the above-given question,
given that,
Brain and Sonya each have a container.
They mark their containers to show tenths.
Brain and Sonya both fill their containers with 0.7 units of juice.