Engage NY Eureka Math 4th Grade Module 5 Lesson 4 Answer Key
Eureka Math Grade 4 Module 5 Lesson 4 Problem Set Answer Key
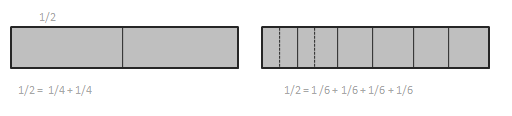
Question 1.
The total length of each tape diagram represents 1. Decompose the shaded unit fractions as the sum of smaller unit fractions in at least two different ways. The first one has been done for you.
a. 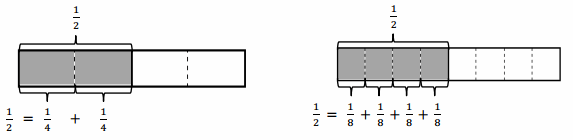
Answer:
1/2 = 1/4 + 1/4 .
1/2 = 1/8 + 1/8 + 1/8 + 1/8.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/2 = 1/4 + 1/4 .
1/2 = 1/8 + 1/8 + 1/8 + 1/8.
b. 
Answer:
1/3 = 1/6 + 1/6.
1/3 = 1/12 + 1/12 + 1/12 + 1/12.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/3 = 1/6 + 1/6.
1/3 = 1/12 + 1/12 + 1/12 + 1/12.
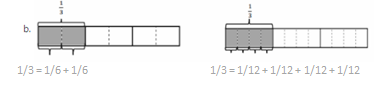
c. 
Answer:
1/4 = 1/8 + 1/8.
1/4 = 1/ 16+ 1/16 + 1/16 + 1/16.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/4 = 1/8 + 1/8.
1/4 = 1/ 16+ 1/16 + 1/16 + 1/16.
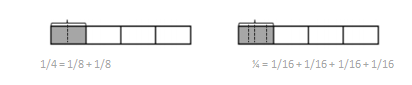
d. 
Answer:
1/5 = 1/10 + 1/10.
1/5 = 1/ 15+ 1/15 + 1/15 + 1/15.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/5 = 1/10 + 1/10.
1/5 = 1/ 15+ 1/15 + 1/15 + 1/15.
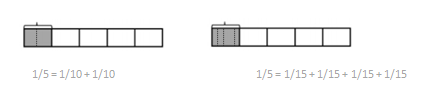
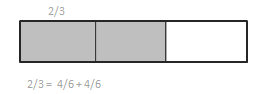
Question 2.
The total length of each tape diagram represents 1. Decompose the shaded fractions as the sum of smaller unit fractions in at least two different ways.
a. 
Answer:
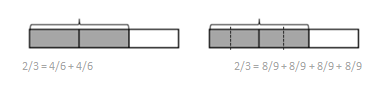
2/3 = 4/6 + 4/6.
2/3 = 8/ 9+ 8/9 + 8/9 + 8/9.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/3 = 4/6 + 4/6.
2/3 = 8/9 + 8/9 + 8/9 + 8/9.
b. 
Answer:
3/5 =6/10 + 6/10.
3/5 = 9/ 15+ 9/15 + 9/15 + 9/15.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
3/5 = 6/10 + 6/10.
3/5 = 9/ 15 + 9/15 + 9/15.
Question 3.
Draw and label tape diagrams to prove the following statements. The first one has been done for you.
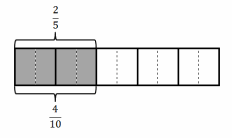
a. \(\frac{2}{5}\) = \(\frac{4}{10}\)
Answer:
2/5 = 4/10 + 4/10.
2/5 = 8/ 20+ 8/20 + 8/20 + 8/20.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/5 = 4/10 + 4/10.
2/5 = 8/ 20+ 8/20 + 8/20 + 8/20
b. \(\frac{2}{6}\) = \(\frac{4}{12}\)
Answer:
2/6 = 4/12 + 4/12.
2/6 = 4/18 + 4/18 + 4/18 + 4/18.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/6 = 4/12 + 4/12.
2/6 = 4/18 + 4/18 + 4/18 + 4/18.

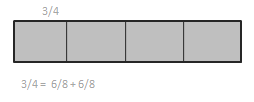
c. \(\frac{3}{4}\) = \(\frac{6}{8}\)
Answer:
3/4 = 6/8 + 6/8.
3/4 = 9/12 + 9/12 + 9/12 + 9/12.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
3/4 = 6/8 + 6/8.
3/4 = 9/12 + 9/12 + 9/12 + 9/12.
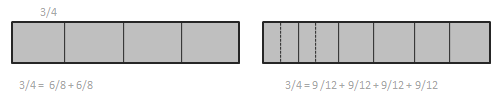
d. \(\frac{3}{4}\) = \(\frac{9}{12}\)
Answer:
3/4 = 6/8 + 6/8.
3/4 = 9/12 + 9/12 + 9/12 + 9/12.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
3/4 = 6/8 + 6/8.
3/4 = 9/12 + 9/12 + 9/12 + 9/12.
Question 4.
Show that \(\frac{1}{2}\) is equivalent to \(\frac{4}{8}\) using a tape diagram and a number sentence.
Answer:
1/2 = 1/4 + 1/4.
1/2 = 1/8 + 1/8 + 1/8 + 1/8 = 4/8.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/2 = 1/4 + 1/4.
1/2 = 1/8 + 1/8 + 1/8 + 1/8 = 4/8.
Question 5.
Show that \(\frac{2}{3}\) is equivalent to \(\frac{6}{9}\) using a tape diagram and a number sentence.
Answer:
2/3 = 4/6 + 4/6.
2/3 = 6/9 + 6/9 + 6/9 + 6/9 = 6/9.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/3 = 4/6 + 4/6.
2/3 = 6/9 + 6/9 + 6/9 + 6/9 = 6/9.

Question 6.
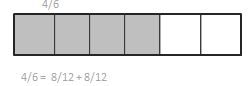
Show that \(\frac{4}{6}\) is equivalent to \(\frac{8}{12}\) using a tape diagram and a number sentence.
Answer:
4/6 = 8/12 + 8/12.
4/6 = 12/18 + 12/18.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
4/6 = 8/12 + 8/12.
4/6 = 12/18 + 12/18.
Engage NY Math 4th Grade Module 5 Lesson 4 Exit Ticket Answer Key
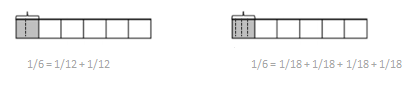
Question 1.
The total length of the tape diagram represents 1. Decompose the shaded unit fraction as the sum of smaller unit fractions in at least two different ways.

Answer:
1/6 = 1/12 + 1/12 .
1/6 = 1/18 + 1/18 + 1/18 + 1/18.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/6 = 1/12 + 1/12 .
1/6 = 1/18 + 1/18 + 1/18 + 1/18.
Question 2.
Draw a tape diagram to prove the following statement.
\(\frac{2}{3}\) = \(\frac{4}{6}\)
Answer:
2/3 = 4/6 + 4/6.
2/3 = 8/12 + 8/12 + 8/12 + 8/12.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/3 = 4/6 + 4/6.
2/3 = 8/12 + 8/12 + 8/12 + 8/12.
Eureka Math 4th Grade Module 5 Lesson 4 Homework Answer Key
Question 1.
The total length of each tape diagram represents 1. Decompose the shaded unit fractions as the sum of smaller unit fractions in at least two different ways. The first one has been done for you.
a. 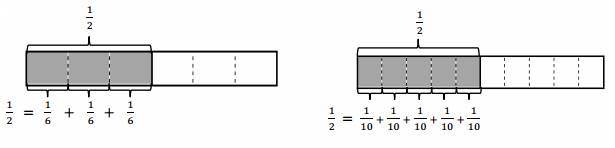
Answer:
1/2 = 1/6 + 1/6 + 1/6.
1/2 = 1/10 + 1/10 + 1/10 + 1/10 + 1/10.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/2 = 1/6 + 1/6 + 1/6.
1/2 = 1/10 + 1/10 + 1/10 + 1/10 + 1/10.
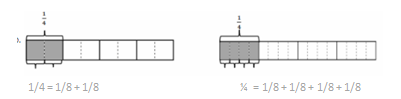
b. 
Answer:
1/4 = 1/8 + 1/8.
1/4 = 1/12 + 1/12 + 1/12 + 1/12.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/4 = 1/8 + 1/8.
1/4 = 1/12 + 1/12 + 1/12 + 1/12.
Question 2.
The total length of each tape diagram represents 1. Decompose the shaded fractions as the sum of smaller unit fractions in at least two different ways.
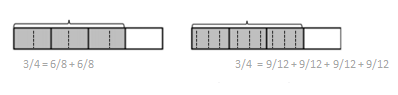
a. 
Answer:
3/4 = 6/8 + 6/8.
3/4 = 9/12 + 9/12 + 9/12 + 9/12.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
3/4 = 6/8 + 6/8.
3/4 = 9/12 + 9/12 + 9/12 + 9/12
b. 
Answer:
4/5 = 8/10 + 8/10.
4/5 = 12/15 + 12/15 + 12/15 + 12/15.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
4/5 = 8/10 + 8/10.
4/5 = 12/15 + 12/15 + 12/15 + 12/15.
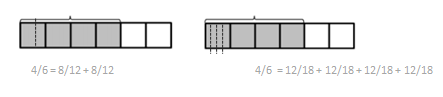
c. 
Answer:
4/6 = 8/12 + 8/12.
4/6 = 12/18 + 12/18 + 12/18 + 12/18.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
4/6 = 8/12 + 8/12.
4/6 = 12/18 + 12/18 + 12/18 + 12/18.
Question 3.
Draw tape diagrams to prove the following statements. The first one has been done for you.
a. \(\frac{2}{5}\) = \(\frac{4}{10}\)
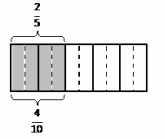
Answer:
2/5 = 4/10 + 4/10.
2/5 = 4/10 + 4/10 + 4/10 + 4/10.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/5 = 4/10 + 4/10.
2/5 = 4/10 + 4/10 + 4/10 + 4/10.
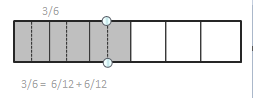
b. \(\frac{3}{6}\) = \(\frac{6}{12}\)
Answer:
3/6 = 6/12 + 6/12.
3/6 = 12/24 + 12/24 + 12/24 + 12/24.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
3/6 = 6/12 + 6/12.
3/6 = 12/24 + 12/24 + 12/24 + 12/24.
c. \(\frac{2}{6}\) = \(\frac{6}{18}\)
Answer:
2/6 = 4/12 + 4/12.
2/6 = 6/18 + 6/18 + 6/18 + 6/18.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/6 = 4/12 + 4/12.
2/6 = 6/18 + 6/18 + 6/18 + 6/18.

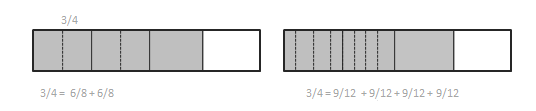
d. \(\frac{3}{4}\) = \(\frac{12}{16}\)
Answer:
3/4 = 6/8 + 6/8.
3/4 = 12/16 + 12/16 + 12/16 + 12/16.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
3/4 = 6/8 + 6/8.
3/4 = 12/16 + 12/16 + 12/16 + 12/16.
Question 4.
Show that \(\frac{1}{2}\) is equivalent to \(\frac{6}{12}\) using a tape diagram and a number sentence.
Answer:
1/2 = 1/4 + 1/4.
1/2 = 1/8 + 1/8 + 1/8 + 1/8.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
1/2 = 1/4 + 1/4.
1/2 = 1/8 + 1/8 + 1/8 + 1/8
Question 5.
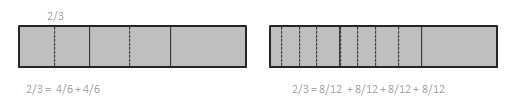
Show that \(\frac{2}{3}\) is equivalent to \(\frac{8}{12}\) using a tape diagram and a number sentence.
Answer:
2/3 = 4/6 + 4/6.
2/3 = 8/12 + 8/12 + 8/12 + 8/12.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
2/3 = 4/6 + 4/6.
2/3 = 8/12 + 8/12 + 8/12 + 8/12.
Question 6.
Show that \(\frac{4}{5}\) is equivalent to \(\frac{12}{15}\) using a tape diagram and a number sentence.
Answer:
4/5 = 8/10 + 8/10.
4/5 = 12/15 + 12/15 + 12/15 + 12/15.
Explanation:
In the above-given question,
given that,
shaded unit fraction as the sum of smaller unit fractions in at least two different ways.
4/5 = 8/10 + 8/10.
4/5 = 12/15 + 12/15 + 12/15 + 12/15.
