Engage NY Eureka Math 4th Grade Module 4 Lesson 4 Answer Key
Eureka Math Grade 4 Module 4 Lesson 4 Problem Set Answer Key
Question 1.
On each object, trace at least one pair of lines that appear to be parallel.
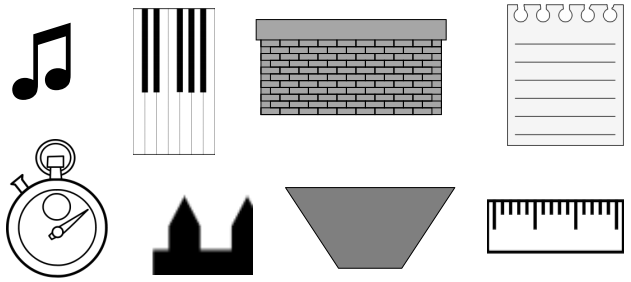
Answer:
As the parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other.
Explanation:
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. These parallel lines are seen in our real-life are zebra crossing, railway tracks, staircases, etc. So in the above image, we have traced the parallel lines to all the images.
Question 2.
How do you know if two lines are parallel?
Answer:
To know the lines are parallel or not, we will see that which are on the same plane are equal at some distance but never meet each other. These parallel lines are seen in our real-life are zebra crossing, railway tracks, staircases, etc. So in the above image, we have traced the parallel lines to all the images.
Question 3.
In the square and triangular grids below, use the given segments in each grid to draw a segment that is parallel using a straightedge.
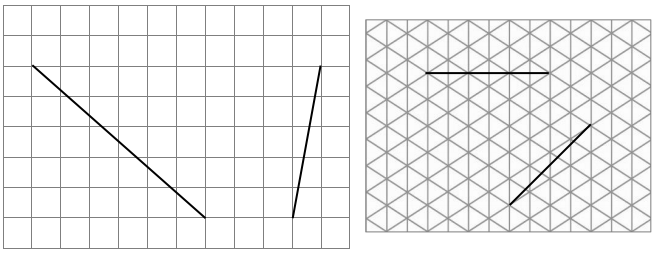
Answer:
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other.
Explanation:
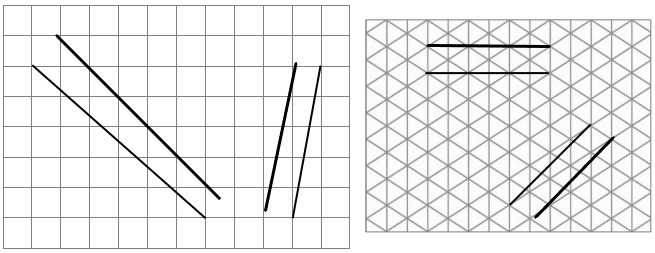
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. These parallel lines are seen in our real-life are zebra crossing, railway tracks, staircases, etc. So in the above image, we have traced the parallel lines to all the images.
Question 4.
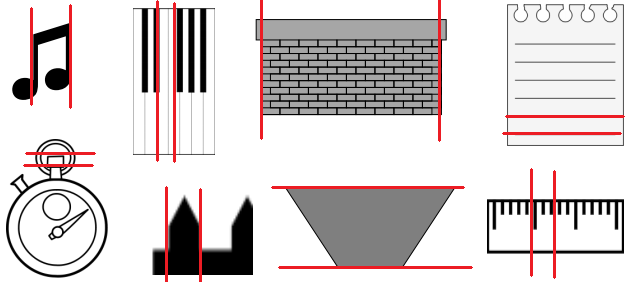
Determine which of the following figures have sides that are parallel by using a straightedge and the right angle template that you created. Circle the letter of the shapes that have at least one pair of parallel sides. Mark each pair of parallel sides with arrowheads, and then identify the parallel sides with a statement modeled after the one in 4(a).
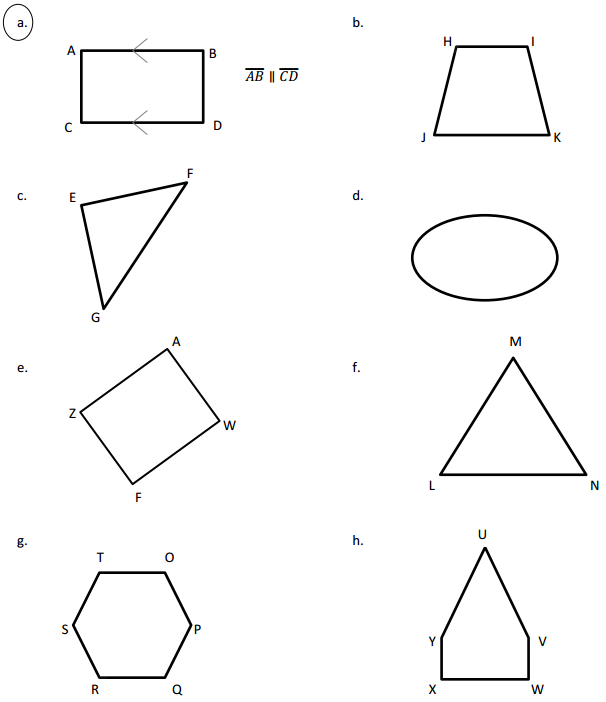
Answer:
The parallel lines in image a are AB and CD and AC and BD.
The parallel lines in image b are HI and JK.
There are no parallel lines in image c.
There are no parallel lines in image d.
The parallel lines in the image e are ZF and AW, ZA and FW.
There are no parallel lines in image f.
The parallel lines in the image g are TO and RQ, ST and QP, RS and OP.
The parallel lines in the image h are YX and VW.
Explanation:
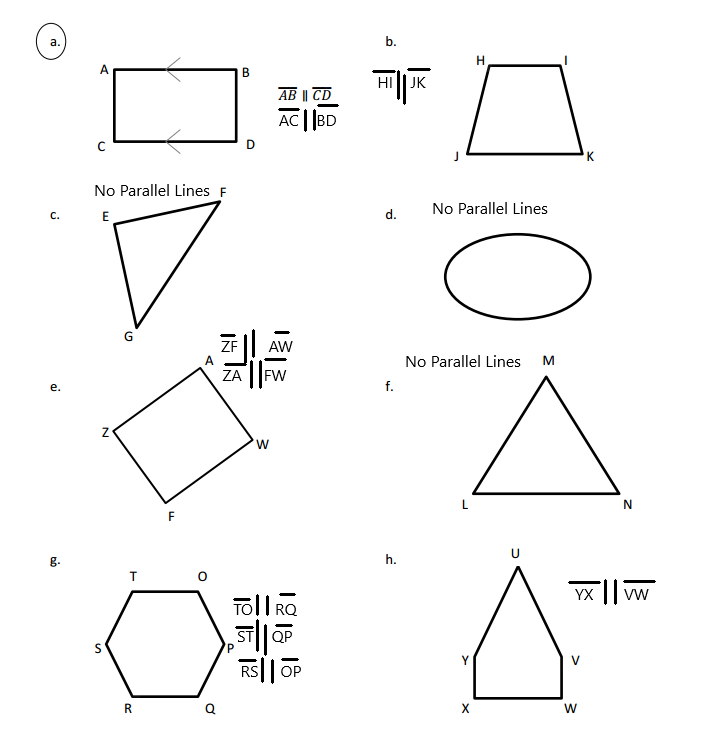
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. These parallel lines are seen in our real-life are zebra crossing, railway tracks, staircases, etc. So the parallel lines in the image we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the parallel lines are AB and CD and AC and BD. In image b we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the parallel lines are HI and JK. In image c we can see that there are no set of two lines that are on the same plane are equal at some distance but never meet each other so there are no parallel lines. In image d we can see that there no set of two lines that are on the same plane that are equal at some distance but never meet each other so there no parallel lines. In image e we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the parallel lines are ZF and AW, ZA and FW. In image f we can see that there are no set of two lines that are on the same plane are equal at some distance but never meet each other so there will be no parallel lines. In image g we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the parallel lines are TO and RQ, ST and QP, RS and OP. In image h we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the YX and VW.
Question 5.
True or false? A triangle cannot have sides that are parallel. Explain your thinking.
Answer:
Yes, it is true. As the triangle does not have a set of two lines that are on the same plane are equal at some distance but never meet each other.
Question 6.
Explain why \(\overline{A B}\) and \(\overline{C D}\) are parallel, but \(\overline{E F}\) and \(\overline{G H}\) are not.

Answer:
Here in the above image, we can see that AB and CD are parallel because there are set of two lines that are on the same plane are equal at some distance but never meet each other. And we did not see the set of two lines that are on the same plane are equal at some distance but never meet each other in EF and Gh so those lines are not parallel.
Question 7.
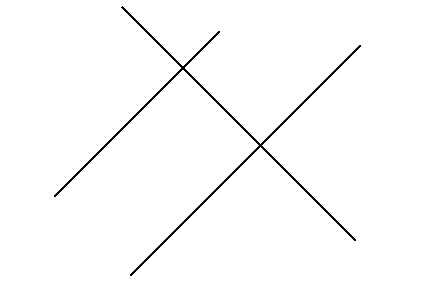
Draw a line using your straightedge. Now, use your right angle template and straightedge to construct a line parallel to the first line you drew.
Answer:
As the parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other.
Explanation:
As the parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. Here, we will draw a line using a straightedge, and then we will use the right-angle template and straightedge to construct a parallel line. So the image will be
Eureka Math Grade 4 Module 4 Lesson 4 Exit Ticket Answer Key
Look at the following pairs of lines. Identify if they are parallel, perpendicular, or intersecting.
Question 1.
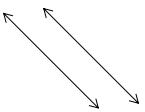
____________________
Answer:
The lines are parallel.
Explanation:
In the above image, there are set of two lines that are on the same plane are equal at some distance but never meet each other. So the lines are parallel lines.
Question 2.
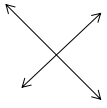
____________________
Answer:
The lines are perpendicular to each other.
Explanation:
When two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. In the above images, we have traced out the perpendicular lines and the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. So those lines are perpendicular.
Question 3.
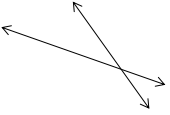
____________________
Answer:
The lines are intersecting each other.
Explanation:
In the above image, we can see that two lines intersect each other, as the two lines cross in a plane and share a common point that exists on all the intersecting lines. So the lines are intersecting each other.
Question 4.
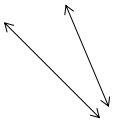
____________________
Answer:
The lines are parallel to each other.
Explanation:
In the above image, there are set of two lines that are on the same plane are equal at some distance but never meet each other. So the lines are parallel lines.
Eureka Math Grade 4 Module 4 Lesson 4 Homework Answer Key
Question 1.
On each object, trace at least one pair of lines that appear to be parallel.
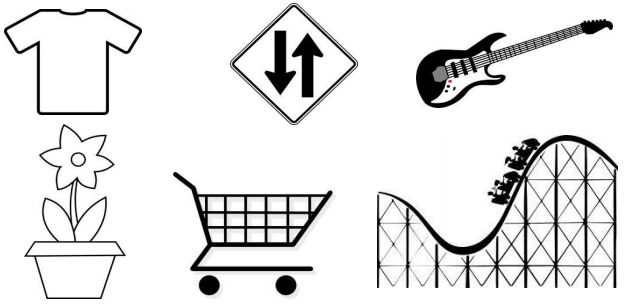
Answer:
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other.
Explanation:
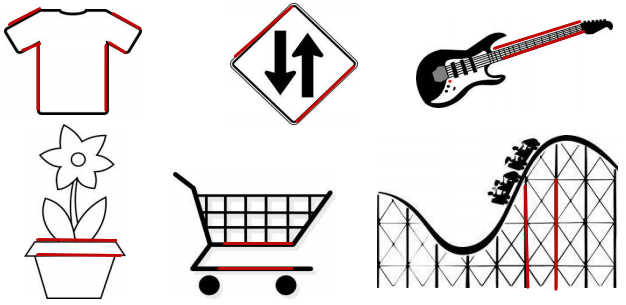
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. These parallel lines are seen in our real-life are zebra crossing, railway tracks, staircases, etc. So in the above image, we have traced the parallel lines to all the images.
Question 2.
How do you know if two lines are parallel?
Answer:
We know that the two lines are parallel by seeing that the set of two lines that are on the same plane are equal at some distance but never meet each other.
Question 3.
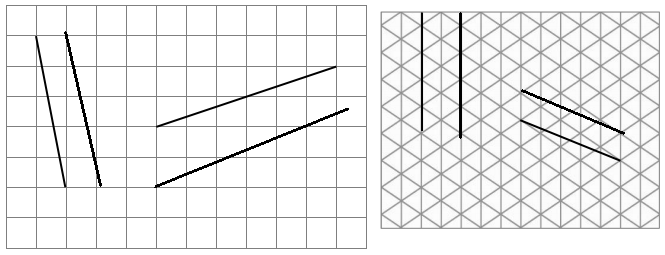
In the square and triangular grids below, use the given segments in each grid to draw a segment that is parallel using a straightedge.
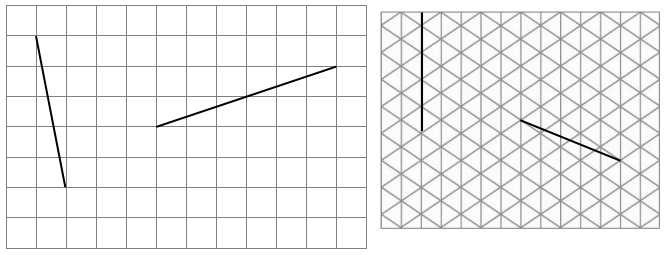
Answer:
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other.
Explanation:
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. These parallel lines are seen in our real-life are zebra crossing, railway tracks, staircases, etc. So in the above image, we have traced the parallel lines to all the images.
Question 4.
Determine which of the following figures have sides that are parallel by using a straightedge and the right angle template that you created. Circle the letter of the shapes that have at least one pair of parallel sides. Mark each pair of parallel sides with arrows, and then identify the parallel sides with a statement modeled after the one in 4(a).
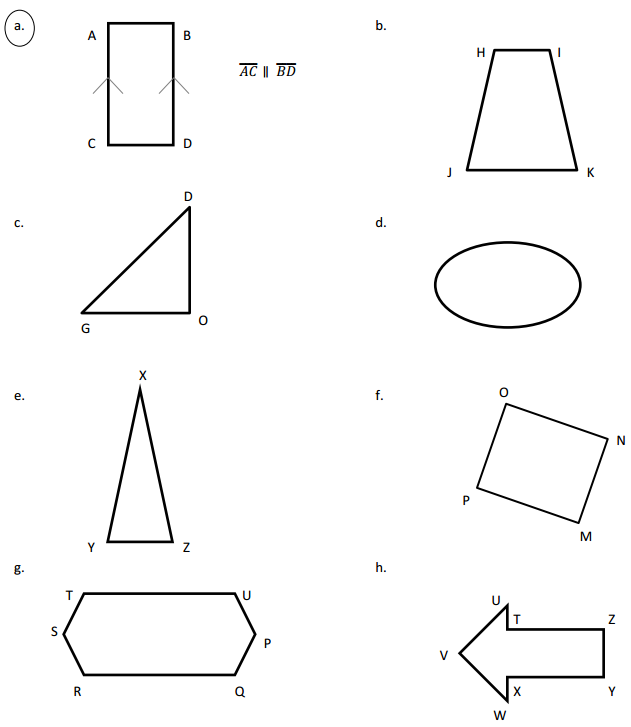
Answer:
The parallel lines in image a are AC and BD.
The parallel lines in image b are HI and JK.
There are no parallel lines in image c.
There are no parallel lines in image d.
There are no parallel lines in image e.
The parallel lines in the image f are OP and NM.
The parallel lines in the image g are ST and QP.
The parallel lines in the image h are UT and ZY.
Explanation:
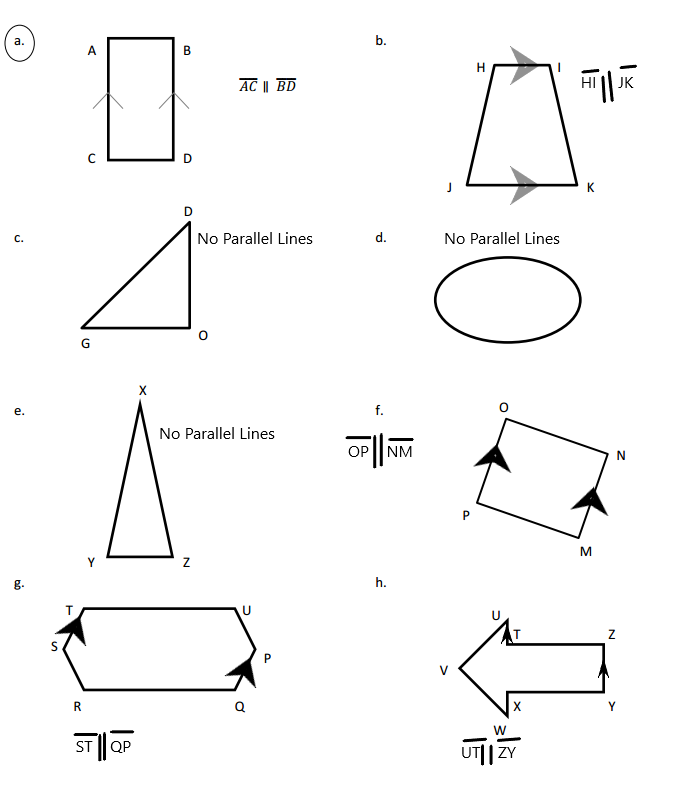
The parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. These parallel lines are seen in our real-life are zebra crossing, railway tracks, staircases, etc. So the parallel lines in the image we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the parallel lines are AC and BD. In image b we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the parallel lines are HI and JK. In image c we can see that there are no set of two lines that are on the same plane are equal at some distance but never meet each other so there are no parallel lines. In image d we can see that there no set of two lines that are on the same plane that are equal at some distance but never meet each other so there no parallel lines. In image e we can see that there are no set of two lines that are on the same plane are equal at some distance but never meet each other so there are no parallel lines. In image f we can see that there are no set of two lines that are on the same plane are equal at some distance but never meet each other so there will be no parallel lines. In image g we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the parallel lines are ST and QP. In image h we can see the set of two lines that are on the same plane are equal at some distance but never meet each other so the UT and ZY.
Question 5.
True or false? All shapes with a right angle have sides that are parallel. Explain your thinking.
Answer:
No, it’s not true. As the right angle does not have a set of two lines that are on the same plane are equal at some distance but never meet each other. So it is false.
Question 6.
Explain why \(\overline{A B}\) and \(\overline{C D}\) are parallel, but \(\overline{E F}\) and \(\overline{G H}\) are not.

Answer:
In the above image, we can see that AB and CD lines are parallel lines, as if we extend the lines they will never intersect. And the lines EF and GH are not parallel as if we extend those lines they will intersect, so these lines are not parallel.
Question 7.
Draw a line using your straightedge. Now, use your right angle template and straightedge to construct a line parallel to the first line you drew.
Answer:
As the parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other.
Explanation:
As the parallel lines are defined as the set of two lines that are on the same plane are equal at some distance but never meet each other. Here, we will draw a line using a straightedge, and then we will use the right-angle template and straightedge to construct a parallel line. So the image will be