Eureka Math Grade 4 Module 3 Lesson 1 Answer Key

Engage NY Eureka Math 4th Grade Module 3 Lesson 1 Answer Key

Eureka Math Grade 4 Module 3 Lesson 1 Problem Set Answer Key

Question 1.
Determine the perimeter and area of rectangles A and B.

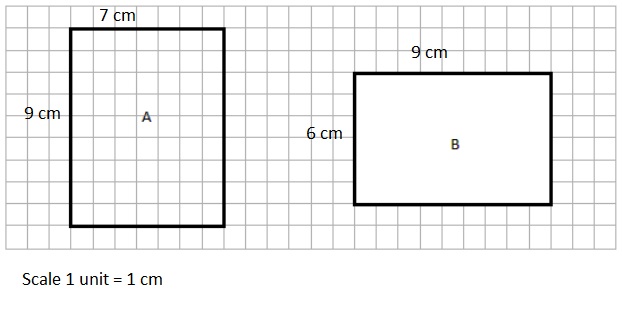
a. A = _____63 cm²__________     A = ______54 cm²_________

b. P = ______32 cm_________     P = ______30 cm_________
Answer:

Answer:
a. A = 63 cm² , A = 54 cm²,

Explanation:
As shown in figure A length = 9 cm , breadth = 7 cm,
Area of rectangle is = l × b = 9 cm × 7 cm = 63 square cm,
and in figure B length = 6 cm , breadth = 9 cm,
Area of rectangle is = l × b = 6 cm × 9 cm = 54 square cm.

b. P = 32 cm,  P = 30 cm,

Explanation:
As shown in figure A length = 9 cm , breadth = 7 cm,
Perimeter of rectangle is =2 × (l + b) = 2(9 cm + 7 cm) =
2 × (16 cm) = 32 cm,
and in figure B length = 6 cm , breadth = 9 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (6 cm + 9 cm) =
2 × (15 cm) = 30 cm.

Question 2.
Determine the perimeter and area of each rectangle.
a.

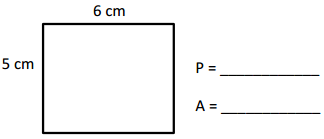
P = _____22 cm_______
A = _____30 cm²_______
Answer:
Perimeter = 22 cm,
Area = 30 cm²,

Explanation:
Given length = 5 cm and breadth = 6 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (5 cm + 6 cm) =
2 × (11 cm) = 22 cm,
Area of rectangle is = l × b = 5 cm × 6 cm = 30 square cm.

b.

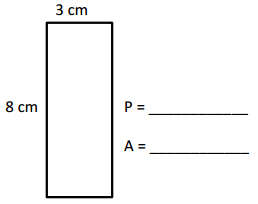
P = ____22 cm_______
A = ____ 24 cm²________
Answer:
Perimeter = 22 cm,
Area = 24 cm²,

Explanation:
Given length = 8 cm and breadth = 3 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (8 cm + 3 cm) =
2 × (11 cm) = 22 cm,
Area of rectangle is = l × b = 8 cm × 3 cm = 24 square cm.

Question 3.
Determine the perimeter of each rectangle.
a.

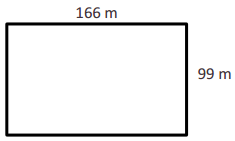
P = ____530 m________
Answer:
Perimeter = 530 m,

Explanation:
Given length = 99 m and breadth = 166 m,
Perimeter of rectangle is =2 × (l + b) = 2 × (99 m + 166 m)
= 2 × ( 265 m) = 530 m.

b.

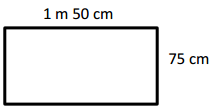
P = ____450 cm________
Answer:
Perimeter =  450 cm,

Explanation:
Given length = 75 cm and breadth = 1 m 50 cm,
we know 1 m = 100 cm ,
so breadth =  1 × 100 cm + 50 cm =150 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (75 cm + 150 cm)
= 2 × (225 cm) = 450 cm.

Question 4.
Given the rectangle’s area, find the unknown side length.
a.

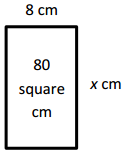
x = ____10 cm________
Answer:
Unknown side length = 10 cm,

Explanation:
Given width of rectangle as 8 cm and area as 80 square cm,
and unknow side length is x cm, we know area of rectangle is
length × breadth, So 80 sq cm = 8 cm × x cm,
So x cm = 80 sq cm ÷ 8 cm = 10 cm,
therefore unknown side length = 10 cm.

b.

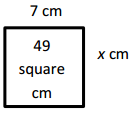
x = ____7 cm________
Answer:
Unknown side length = 7 cm,

Explanation:
Given width of rectangle as 7 cm and area as 49 square cm,
and unknow side length is x cm, we know area of rectangle is
length × breadth, So 49 sq cm = 7 cm × x cm,
So x cm = 49 sq cm ÷ 7 cm = 7 cm,
therefore unknown side length = 7 cm.

Question 5.
Given the rectangle’s perimeter, find the unknown side length.
a. P = 120 cm

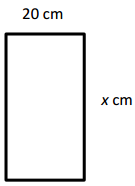
Answer:
Unknown side length = 40 cm,

Explanation:
Given width of rectangle as 20 cm and perimeter as 120 cm,
and unknow side length is x cm, we know perimeter of
rectangle is 2 × (length + breadth),
So 120 cm = 2 × (x cm + 20 cm),
120 cm ÷ 2 = (x cm + 20 cm),
60 cm = (x cm + 20 cm),
So x cm = 60 cm – 20 cm = 40 cm,
therefore unknown side length = 40 cm.

b. p = 1000 m

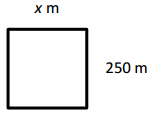
Answer:
Unknown side width = 250 m,

Explanation:
Given length of rectangle as 250 m and perimeter as 1000 m,
and unknow side width is x m, we know perimeter of
rectangle is 2 × (length + breadth),
So 1000 m = 2 × (250 m + x m),
1000 m ÷ 2 = (250 m + x m ),
500 m = 250 m + x m ,
So x m = 500 m – 250 m = 250 m,
therefore unknown side length = 250 m.

Question 6.
Each of the following rectangles has whole number side lengths.
Given the area and perimeter, find the length and width.
a. P = 20 cm

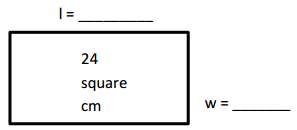
Answer:
The whole number side lengths are
If the length of the rectangle is 4 cm then the width is 6 cm or
length of the rectangle is 6 cm then the width is 4 cm,

Explanation:
Given area = 24 square cm and perimeter = 20 cm of rectangles,
lets take length as l and width as w and we know
area of rectangle = length × width , 24 sq cm = l × w and
perimeter = 2 × (length + width) ,
20 cm = 2 × ( l + w), l + w = 20 cm ÷ 2 =10 cm,
so l = 10 cm – w, now 24 = (10 – w) × w,
we get w²– 10 w + 24 = 0,
So w²– 6 w – 4 w + 24 = 0,
w(w – 6) – 4(w – 6) = 0, therefore w = 6 cm or w = 4 cm,
So l = 10 cm – 6 cm = 4 cm or l = 10 cm  – 4 cm = 6 cm,
Therfore, If length of rectangle is 4 cm then width is 6 cm or
length of rectangle is 6 cm then width is 4 cm.

b. P = 28 m

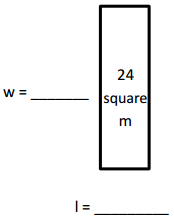
Answer:
The whole number side lengths are
If the length of the rectangle is 2 m then the width is 12 m or
The length of the rectangle is 12 m the width is 2 m.

Explanation:
Given area = 24 square m and perimeter = 28 m of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 24 sq m = l X w and
perimeter = 2 × (length + width) ,
28 m = 2 × ( l + w), l + w = 28 m ÷ 2 =14 m,
so l = 14 m – w, now 24 = (14 – w) × w,
we get w²– 14 w + 24 = 0,
So w²– 12 w – 2 w + 24 = 0,
w(w – 12) – 2(w – 12) = 0, therefore w = 12 m or w = 2 m,
So l = 14 m – 12 m = 2 m or l = 14 m – 2 m = 12 m,
Therfore, If length of rectangle is 2 m then width is 12 m or
length of rectangle is 12 m then width is 2 m.

Eureka Math Grade 4 Module 3 Lesson 1 Exit Ticket Answer Key

Question 1.
Determine the area and perimeter of the rectangle.

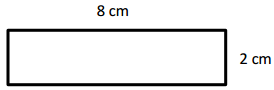
Answer:
Area = 16 cm²,
Perimeter = 20 cm,

Explanation:
Given length = 8 cm and breadth = 2 cm,
Area of rectangle is = l × b = 8 cm × 2 cm = 16 square cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (8 cm + 2 cm) =
2 × (10 cm) = 20 cm.

Question 2.
Determine the perimeter of the rectangle.

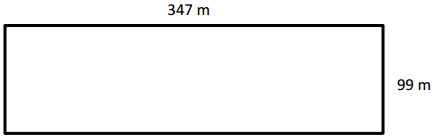
Answer:
Perimeter = 892 m,

Explanation:
Given length = 347 m and breadth = 99 m,
Perimeter of rectangle is =2 × (l + b) = 2 × (347 m + 99 m) =
2 × (446 m) = 892 m.

Eureka Math Grade 4 Module 3 Lesson 1 Homework Answer Key

Question 1.
Determine the perimeter and area of rectangles A and B.

a. A = _____40 cm²__________    A = ______35 cm²_________

b. P = ______26 cm_________    P = _______24 cm________
Answer:

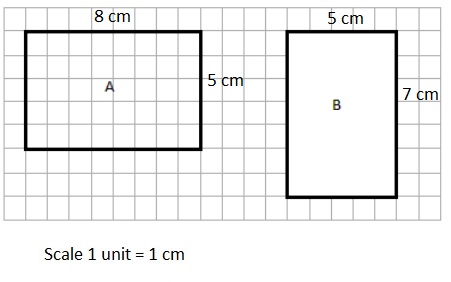
a. A = 40 cm² , A = 35 cm²,

Explanation:
As shown in figure A length = 8 cm , breadth = 5 cm,
Area of rectangle is = l × b = 8 cm × 5 cm = 40 square cm,
and in figure B length = 5 cm , breadth = 7 cm,
Area of rectangle is = l × b = 5 cm × 7 cm = 35 square cm,

b. P = 26 cm,  P = 24 cm,

Explanation:
As shown in figure A length = 8 cm , breadth = 5 cm,
Perimeter of rectangle is =2 × (l + b) = 2(8 cm + 5 cm) =
2 × (13 cm) = 26 cm,
and in figure B length = 5 cm , breadth = 7 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (5 cm + 7 cm) =
2 × (12 cm) = 24 cm.

Question 2.
Determine the perimeter and area of each rectangle.
a.

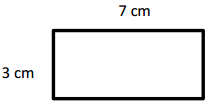
P = ____20 cm________
A = ___ 21 cm²____
Answer:
Perimeter = 20 cm,
Area = 21 cm²,

Explanation:
Given length = 7 cm and breadth = 3 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (7 cm + 3 cm) =
2 × (10 cm) = 20 cm,
Area of rectangle is = l × b = 7 cm × 3 cm = 21 square cm,

b.

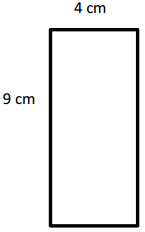
P = ___26 cm_________
A = ______36 cm²______
Answer:
Perimeter = 26 cm,
Area = 36 cm²,

Explanation:
Given length = 9 cm and breadth = 4 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (9 cm + 4 cm) =
2 × (13 cm) = 26 cm,
Area of rectangle is = l × b = 9 cm × 4 cm = 36 square cm,

Question 3.
Determine the perimeter of each rectangle.
a.

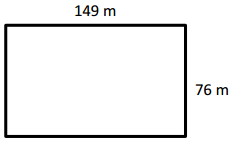
P = _____850 m_______
Answer:
Perimeter = 850 m,

Explanation:
Given length = 76 m and breadth = 149 m,
Perimeter of rectangle is =2 × (l + b) = 2 × (76 m + 149 cm) =
2 × ( 425 m) = 850 m.

b.

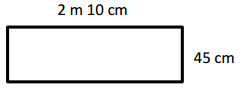
P = ____510 cm________
Answer:
Perimeter =  510 cm,

Explanation:
Given length = 45 cm and breadth = 2 m 10 cm,
we know 1 m = 100 cm ,
so breadth =  2 × 100 cm + 10 cm = 200 cm + 10 cm = 210 cm,
Perimeter of rectangle is =2 × (l + b) = 2 × (45 cm + 210 cm) =
2 × (255 cm) = 510 cm.

Question 4.
Given the rectangle’s area, find the unknown side length.
a.

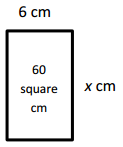
x = _____10 cm_______
Answer:
Unknown side length = 10 cm,

Explanation:
Given width of rectangle as 6 cm and area as 60 square cm,
and unknow side length is x cm, we know area of rectangle is
length × breadth, So 60 sq cm = 6 cm × x cm,
So x cm = 60 sq cm ÷ 6 cm = 10 cm,
therefore unknown side length = 10 cm.

b.

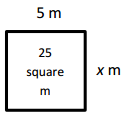
x = _____5 m_______
Answer:
Unknown side length = 5 m,

Explanation:
Given width of rectangle as 5 m and area as 25 square m,
and unknown side length is x m, we know the area of the rectangle is length × breadth, So 25 sq m = 5 m × x m,
So x m = 25 sq m ÷ 5 m = 5 m,
therefore unknown side length = 5 m.

Question 5.
Given the rectangle’s perimeter, find the unknown side length.
a. P = 180 cm

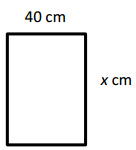
x = ____40 cm________
Answer:
Unknown side length = 40 cm,

Explanation:
Given width of rectangle as 40 cm and perimeter as 180 cm,
and unknow side length is x cm, we know perimeter of
rectangle is 2 × (length + breadth),
So 180 cm = 2 × (x cm + 40 cm),
180 cm ÷ 2 = (x cm + 40 cm),
90 cm = (x cm + 40 cm),
So x cm = 90 cm – 40 cm = 50 cm,
therefore unknown side length = 50 cm.

b. P = 1,000 m

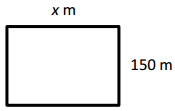
x = ____350 m________
Answer:
Unknown side width = 350 m,

Explanation:
Given length of rectangle as 150 m and perimeter as 1000 m,
and unknow side width is x m, we know perimeter of
rectangle is 2 X (length + breadth),
So 1000 m = 2 X (150 m + x m),
1000 m ÷ 2 = (150 m + x m ),
500 m = 150 m + x m ,
So x m = 500 m – 150 m = 350 m,
therefore unknown side length = 350 m.

Question 6.
Each of the following rectangles has whole number side lengths. Given the area and perimeter, find the length and width.
a. A = 32 square cm
P = 24 cm

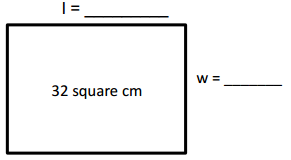
Answer:
The whole number side lengths are
If the length of the rectangle is 4 cm then the width is 8 cm or
length of the rectangle is 8 cm then the width is 4 cm,

Explanation:
Given area = 32 square cm and perimeter = 24 cm of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 32 sq cm = l X w and
perimeter = 2 × (length + width) ,
24 cm = 2 × ( l + w), l + w = 24 cm ÷ 2 =12 cm,
so l = 12 cm – w, now 32 = (12 – w) × w,
we get w²– 12 w + 32 = 0,
So w²– 8 w – 4 w + 32 = 0,
w(w – 8) – 4(w – 8) = 0, therefore w = 8 cm or w = 4 cm,
So l = 12 cm – 8 cm = 4 cm or l = 12 cm  – 4 cm = 8 cm,
Therfore, If length of recatangle is 4 cm then width is 8 cm or
length of rectangle is 8 cm then width is 4 cm.

b. A = 36 square m
P = 30 m

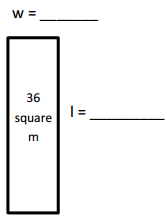
Answer:
The whole number side lengths are
If the length of the rectangle is 3 m then the width is 12 m or
The length of the rectangle is 12 m the width is 3 m.

Explanation:
Given area = 36 square m and perimeter = 30 m of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 36 sq m = l X w and
perimeter = 2 × (length + width) ,
30 m = 2 × ( l + w), l + w = 30 m ÷ 2 =15 m,
so l = 15 m – w, now 36 = (15 – w) X w,
we get w²– 15 w + 36 = 0,
So w²– 12 w – 3 w + 24 = 0,
w(w – 12) – 3(w – 12) = 0, therefore w = 12 m or w = 3 m,
So l = 15 m – 12 m = 3 m or l = 15 m – 3 m = 12 m,
Therfore, If length of rectangle is 3 m then width is 12 m or length of rectangle is 12 m then width is 3 m.