Engage NY Eureka Math 3rd Grade Module 7 Lesson 29 Answer Key
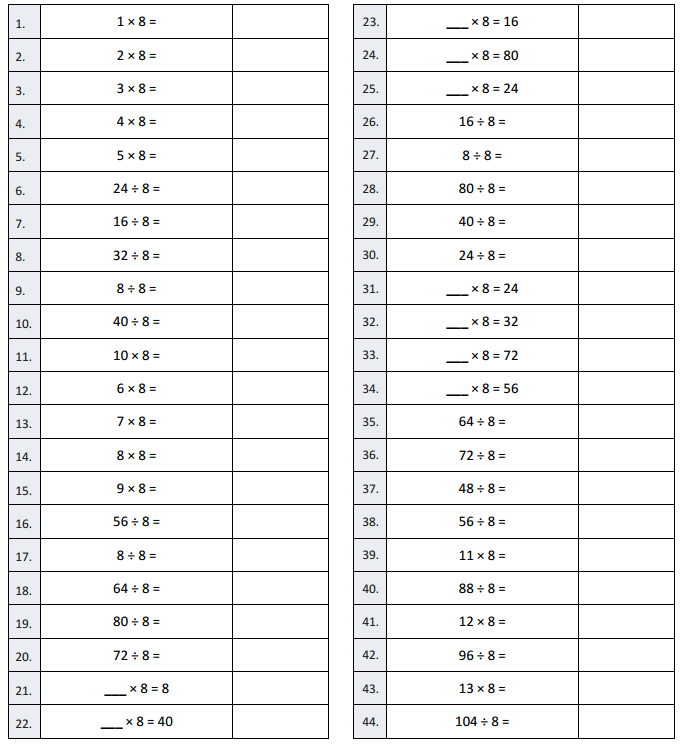
Eureka Math Grade 3 Module 7 Lesson 29 Sprint Answer Key
A
Multiply or Divide by 8

Answer:

Question 1.
2 × 8 =
Answer:
2 × 8 = 16.
Question 2.
3 × 8 =
Answer:
3 × 8 = 24.
Question 3.
4 × 8 =
Answer:
4 × 8 = 32.
Question 4.
5 × 8 =
Answer:
5 × 8 = 40.
Question 5.
1 × 8 =
Answer:
1 × 8 = 8.
Question 6.
16 ÷ 8 =
Answer:
16 ÷ 8 = 2.
Question 7.
24 ÷ 8 =
Answer:
24 ÷ 8 = 3.
Question 8.
40 ÷ 8 =
Answer:
40 ÷ 8 = 5.
Question 9.
8 ÷ 8 =
Answer:
8 ÷ 8 = 1.
Question 10.
32 ÷ 8 =
Answer:
32 ÷ 8 = 4.
Question 11.
6 × 8 =
Answer:
6 × 8 = 48.
Question 12.
7 × 8 =
Answer:
7 × 8 = 56.
Question 13.
8 × 8 =
Answer:
8 × 8 = 64.
Question 14.
9 × 8 =
Answer:
9 × 8 = 72.
Question 15.
10 × 8 =
Answer:
10 × 8 = 80.
Question 16.
64 ÷ 8 =
Answer:
64 ÷ 8 = 8.
Question 17.
56 ÷ 8 =
Answer:
56 ÷ 8 = 7.
Question 18.
72 ÷ 8 =
Answer:
72 ÷ 8 = 9.
Question 19.
48 ÷ 8 =
Answer:
48 ÷ 8 = 6.
Question 20.
80 ÷ 8 =
Answer:
80 ÷ 8 = 10.
Question 21.
___ × 8 = 40
Answer:
5 × 8 = 40.
Question 22.
___ × 8 = 8
Answer:
1 × 8 = 8.
Question 23.
___ × 8 = 80
Answer:
10 × 8 = 80.
Question 24.
___ × 8 = 16
Answer:
2 × 8 = 16.
Question 25.
___ × 8 = 24
Answer:
3 × 8 = 24.
Question 26.
80 ÷ 8 =
Answer:
80 ÷ 8 = 10.
Question 27.
40 ÷ 8 =
Answer:
40 ÷ 8 = 5.
Question 28.
8 ÷ 8 =
Answer:
8 ÷ 8 = 1.
Question 29.
16 ÷ 8 =
Answer:
16 ÷ 8 = 2.
Question 30.
24 ÷ 8 =
Answer:
24 ÷ 8 = 3.
Question 31.
___ × 8 = 48
Answer:
6 × 8 = 48.
Question 32.
___ × 8 = 56
Answer:
7 × 8 = 56.
Question 33.
___ × 8 = 72
Answer:
9 × 8 = 72.
Question 34.
___ × 8 = 64
Answer:
8 × 8 = 64.
Question 35.
56 ÷ 8 =
Answer:
56 ÷ 8 = 7.
Question 36.
72 ÷ 8 =
Answer:
72 ÷ 8 = 9.
Question 37.
48 ÷ 8 =
Answer:
48 ÷ 8 = 6.
Question 38.
64 ÷ 8 =
Answer:
64 ÷ 8 = 8.
Question 39.
11 × 8 =
Answer:
11 × 8 = 88.
Question 40.
88 ÷ 8 =
Answer:
88 ÷ 8 = 11.
Question 41.
12 × 8 =
Answer:
12 × 8 = 96.
Question 42.
96 ÷ 8 =
Answer:
96 ÷ 8 = 12.
Question 43.
14 × 8 =
Answer:
14 × 8 = 112.
Question 44.
112 ÷ 8 =
Answer:
112 ÷ 8 = 14.
B
Multiply or Divide by 8
Answer:
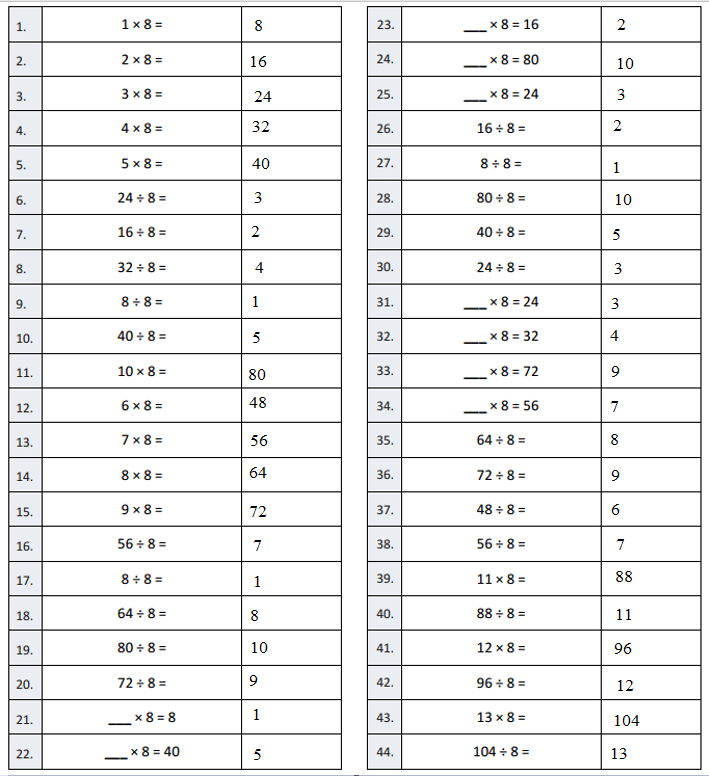
Question 1.
1× 8 =
Answer:
1× 8 = 8.
Question 2.
2 × 8 =
Answer:
2 × 8 = 16.
Question 3.
3 × 8 =
Answer:
3 × 8 = 24.
Question 4.
4 × 8 =
Answer:
4 × 8 = 32.
Question 5.
5 × 8 =
Answer:
5 × 8 = 40.
Question 6.
24 ÷ 8 =
Answer:
24 ÷ 8 = 3.
Question 7.
16 ÷ 8 =
Answer:
16 ÷ 8 = 2.
Question 8.
32 ÷ 8 =
Answer:
32 ÷ 8 = 4.
Question 9.
8 ÷ 8 =
Answer:
8 ÷ 8 = 1.
Question 10.
40 ÷ 8 =
Answer:
40 ÷ 8 = 5.
Question 11.
10 × 8 =
Answer:
10 × 8 = 80.
Question 12.
6 × 8 =
Answer:
6 × 8 = 48.
Question 13.
7 × 8 =
Answer:
7 × 8 = 56.
Question 14.
8 × 8 =
Answer:
8 × 8 = 64.
Question 15.
9 × 8 =
Answer:
9 × 8 = 72.
Question 16.
56 ÷ 8 =
Answer:
56 ÷ 8 = 7.
Question 17.
8 ÷ 8 =
Answer:
8 ÷ 8 = 1.
Question 18.
64 ÷ 8 =
Answer:
64 ÷ 8 = 8.
Question 19.
80 ÷ 8 =
Answer:
80 ÷ 8 = 10.
Question 20.
72 ÷ 8 =
Answer:
72 ÷ 8 = 9.
Question 21.
___ × 8 = 8
Answer:
1 × 8 = 8.
Question 22.
___ × 8 = 40
Answer:
5 × 8 = 40.
Question 23.
___ × 8 = 16
Answer:
2 × 8 = 16.
Question 24.
___ × 8 = 80
Answer:
10 × 8 = 80.
Question 25.
___ × 8 = 24
Answer:
3 × 8 = 24.
Question 26.
16 ÷ 8 =
Answer:
16 ÷ 8 = 2.
Question 27.
8 ÷ 8 =
Answer:
8 ÷ 8 = 1.
Question 28.
80 ÷ 8 =
Answer:
80 ÷ 8 = 10.
Question 29.
40 ÷ 8 =
Answer:
40 ÷ 8 = 5.
Question 30.
24 ÷ 8 =
Answer:
24 ÷ 8 = 3.
Question 31.
___ × 8 = 24
Answer:
3 × 8 = 24.
Question 32.
___ × 8 = 32
Answer:
4 × 8 = 32.
Question 33.
___ × 8 = 72
Answer:
9 × 8 = 72.
Question 34.
___ × 8 = 56
Answer:
7 × 8 = 56.
Question 35.
64 ÷ 8 =
Answer:
64 ÷ 8 = 8.
Question 36.
72 ÷ 8 =
Answer:
72 ÷ 8 = 9.
Question 37.
48 ÷ 8 =
Answer:
48 ÷ 8 = 6.
Question 38.
56 ÷ 8 =
Answer:
56 ÷ 8 = 7.
Question 39.
11 × 8 =
Answer:
11 × 8 = 88.
Question 40.
88 ÷ 8 =
Answer:
88 ÷ 8 = 11.
Question 41.
12 × 8 =
Answer:
12 × 8 = 96.
Question 42.
96 ÷ 8 =
Answer:
96 ÷ 8 = 12.
Question 43.
13 × 8 =
Answer:
13 × 8 = 104.
Question 44.
104 ÷ 8 =
Answer:
104 ÷ 8 = 13.
Eureka Math Grade 3 Module 7 Lesson 29 Problem Set Answer Key
Question 1.
Kyle puts two rectangles together to make the L-shaped figure below. He measures some of the side lengths and records them as shown.
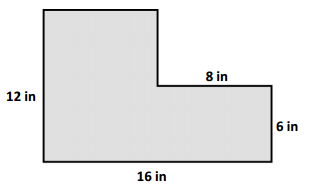
a. Find the perimeter of Kyle’s shape.
b. Find the area of Kyle’s shape.
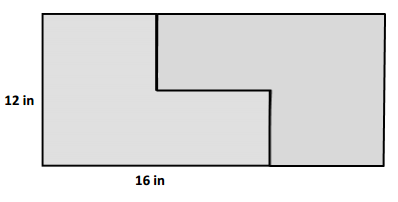
c. Kyle makes two copies of the L-shaped figure to create the rectangle shown below. Find the perimeter of the rectangle.
Answer:
a. Perimeter of ABCDEF Kyle’s shape = 56 in.
b. Area of ABCDEF Kyle’s shape = 144 in.
c. Perimeter of ABCD rectangle = 56 in.
Explanation:
a. 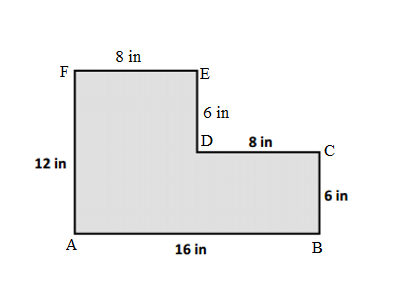
Length of AB side of ABCDEF Kyle’s shape = 16 in
Length of BC side of ABCDEF Kyle’s shape = 6 in
Length of CD side of ABCDEF Kyle’s shape = 8 in
Length of DE side of ABCDEF Kyle’s shape = 6 in
Length of EF side of ABCDEF Kyle’s shape = 8 in
Length of FA side of ABCDEF Kyle’s shape = 12 in
Perimeter of ABCDEF Kyle’s shape = Length of AB side of ABCDEF Kyle’s shape + Length of BC side of ABCDEF Kyle’s shape + Length of CD side of ABCDEF Kyle’s shape + Length of DE side of ABCDEF Kyle’s shape + Length of EF side of ABCDEF Kyle’s shape +
Length of FA side of ABCDEF Kyle’s shape
= 16 in + 6 in + 8 in + 6 in + 8 in + 12 in
= 22 in + 8 in + 6 in + 8 in + 12 in
= 30 in + 6 in + 8 in + 12 in
= 36 in + 8 in + 12 in
= 44 in + 12 in
= 56 in.
b. 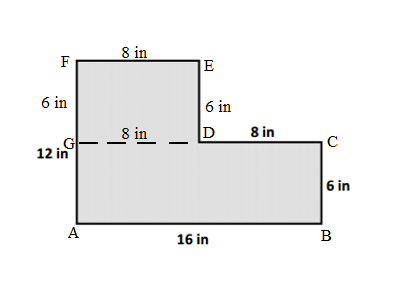
Length of ABCG Kyle’s shape = 16 in
Width of ABCG Kyle’s shape = 6 in
Area of ABCG Kyle’s shape = Length × Width
= 16 in × 6 in
= 96 in.
Length of DEFG Kyle’s shape = 8 in
Width of DEFG Kyle’s shape = 6 in
Area of DEFG Kyle’s shape = Length × Width
= 8 in × 6 in
= 48 in.
Area of ABCDEF Kyle’s shape = Area of ABCG Kyle’s shape + Area of DEFG Kyle’s shape
= 96 in + 48 in
= 144 in.
c. 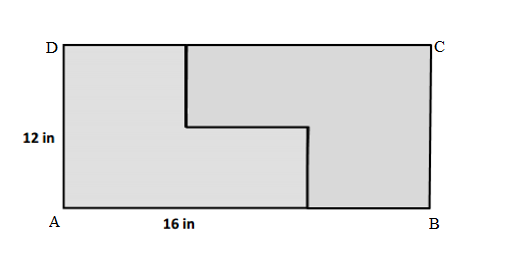
Length of ABCD rectangle = 16 in
Width of ABCD rectangle = 12 in
Perimeter of ABCD rectangle = 2 ( Length + Width )
= 2 ( 16 in + 12 in )
= 2 × 28 in
= 56 in.
Question 2.
Jeremiah and Hayley use a piece of rope to mark a square space for their booth at the science fair. The area of their space is 49 square feet. What is the length of the rope that Jeremiah and Hayley use if they leave a 3-foot opening so they can get in and out of the space?
Answer:
Length of the rope that Jeremiah and Hayley use if they leave a 3-foot opening so they can get in and out of the space = 25 feet.
Explanation:
Area of the square space = 49 square feet.
Area of the square space = Side × Side
= 49 square feet = 7 feet × 7 feet
Length of the rope that Jeremiah and Hayley = 7 feet.
Length of the rope that Jeremiah and Hayley use if they leave a 3-foot opening so they can get in and out of the space = (4 × Length of the rope that Jeremiah and Hayley) – 3 foot
= 28 feet – 3 foot
= 25 feet.
Question 3.
Vivienne draws four identical rectangles as shown below to make a new, larger rectangle. The perimeter of one of the small rectangles is 18 centimeters, and the length is 6 centimeters. What is the perimeter of the new, larger rectangle?
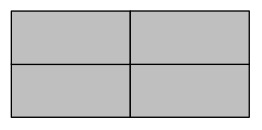
Answer:
Perimeter of the new, larger rectangle = 36 cm.
Explanation:
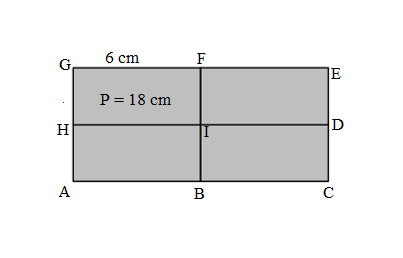
Width of the small rectangle = ??
Length of the small rectangle = 6 cm
Perimeter of the small rectangle = 2 ( Length + Width )
=> 18 cm = 2 ( 6 cm + Width )
=> 18 cm = 12 cm + 2 Width
=> 18 cm – 12 cm = 2 Width
=> 6 cm = 2 Width
=>6 cm ÷ 2 = Width
= 3 cm = Width.
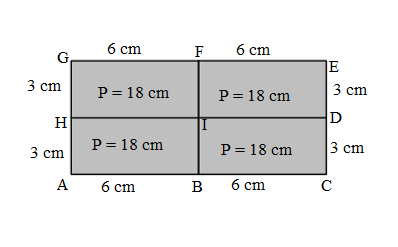
Length of ACEG larger Rectangle = AB + BC = 6 cm + 6 cm = 12 cm.
Width of ACEG larger Rectangle = ED + DC = 3 cm + 3 cm = 6 cm.
Perimeter of the new, larger rectangle = 2 ( Length + Width )
= 2 ( 12 cm + 6 cm )
= 2 × 18 cm
= 36 cm.
Question 4.
A jogging path around the outside edges of a rectangular playground measures 48 yards by 52 yards. Maya runs 3\(\frac{1}{2}\) laps on the jogging path. What is the total number of yards Maya runs?
Answer:
The total number of yards Maya runs = 700 yards.
Explanation:

Length of the jogging rectangular playground = 52 yards
Width of the jogging rectangular playground = 48 yards
Perimeter of the jogging rectangular playground = 2 ( Length + Width )
= 2 ( 52 yards + 48 yards )
= 2 × 100 yards
= 200 yards.
Half of Perimeter of the jogging rectangular playground = 200 yards ÷ 2 = 100 yards.
Perimeter of 3\(\frac{1}{2}\) = (3 × Perimeter of the jogging rectangular playground ) + Half of Perimeter of the jogging rectangular playground
= (3 × 200 yards) + 100 yards
= 600 yards + 100 yards
= 700 yards.
Eureka Math Grade 3 Module 7 Lesson 29 Exit Ticket Answer Key
Jeannette draws four identical squares as shown below to make a new, larger square. The length of one of the small square sides is 8 centimeters. What is the perimeter of the new, larger square?
Answer:
Perimeter of ACEG Jeannette new, larger square = 64 cm.
Explanation:
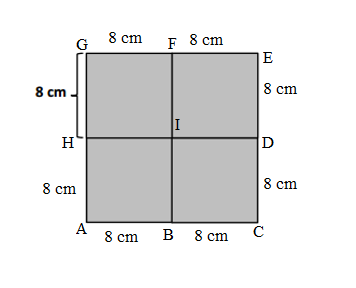
Length of AC side the ACEG Jeannette new, larger square = AB + BC = 8 cm + 8 cm = 16 cm.
Length of CE side the ACEG Jeannette new, larger square = CD + DE = 8 cm + 8 cm = 16 cm.
Length of EG side the ACEG Jeannette new, larger square = EF + FG = 8 cm + 8 cm = 16 cm.
Length of GA side the ACEG Jeannette new, larger square = GH + HA = 8 cm + 8 cm = 16 cm.
Perimeter of ACEG Jeannette new, larger square = Length of AC side the ACEG new, larger square + Length of CE side the ACEG new, larger square + Length of EG side the ACEG new, larger square + Length of GA side the ACEG new, larger square
= 16 cm + 16 cm + 16 cm + 16 cm
= 32 cm + 16 cm + 16 cm
= 48 cm + 16 cm
= 64 cm.
Eureka Math Grade 3 Module 7 Lesson 29 Homework Answer Key
Question 1.
Katherine puts two squares together to make the rectangle below. The side lengths of the squares measure 8 inches.
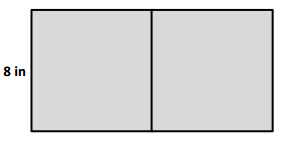
a. What is the perimeter of the rectangle Katherine made with her 2 squares?
b. What is the area of Katherine’s rectangle?
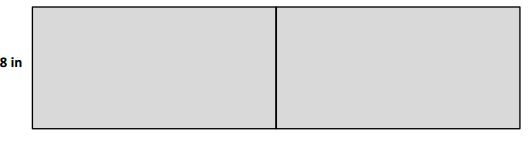
c. Katherine decides to draw another rectangle of the same size. What is the area of the new, larger rectangle?
Answer:
a. Perimeter of the ACDF Katherine’s rectangle = 32 in.
b. Area of the ACDF Katherine’s rectangle = 64 square in.
c. Area of the OQRT new, Katherine’s larger rectangle = 64 square in.
Explanation:
a. 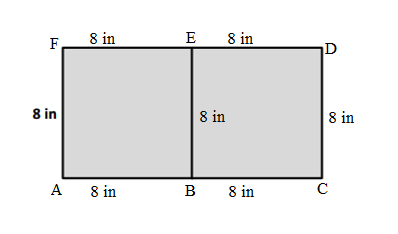
Length of the AC side of ACDF Katherine’s rectangle = 8 in
Length of the CD side of ACDF Katherine’s rectangle = 8 in
Length of the DF side of ACDF Katherine’s rectangle = 8 in
Length of the AF side of ACDF Katherine’s rectangle = 8 in
Perimeter of ACDF Katherine’s rectangle = Length of the AC side of ACDF Katherine’s rectangle + Length of the CD side of ACDF Katherine’s rectangle + Length of the DF side of ACDF Katherine’s rectangle + Length of the AF side of ACDF Katherine’s rectangle
= 8 in + 8 in + 8 in + 8 in
= 16 in + 8 in + 8 in
= 24 in + 8 in
= 32 in.
b. Length of the AC side of the ACDF Katherine’s rectangle = 8 in
Width of the side FG of the ACDF Katherine’s rectangle = 8 in
Area of the ACDF Katherine’s rectangle = Length × Width
= 8 in × 8 in
= 64 square in.
c. 
Length of the OQ side of the OQRT new, Katherine’s larger rectangle = 8 in
Width of the QR side of the OQRT new, Katherine’s larger rectangle = 8 in
Area of the OQRT new, Katherine’s larger rectangle = Length × Width
= 8 in × 8 in
= 64 square in.
Question 2.
Daryl draws 6 equal-sized rectangles as shown below to make a new, larger rectangle. The area of one of the small rectangles is 12 square centimeters, and the length of the small rectangle is 4 centimeters..
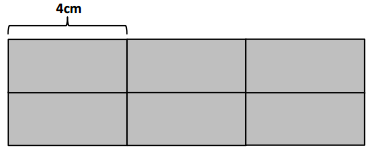
a. What is the perimeter of Daryl’s new rectangle?
b. What is the area of Daryl’s new rectangle?
Answer:
a. Perimeter of the ADFI Daryl’s new rectangle = 36cm.
b. Area of the ADFI Daryl’s new rectangle = 72 square cm.
Explanation:
a. 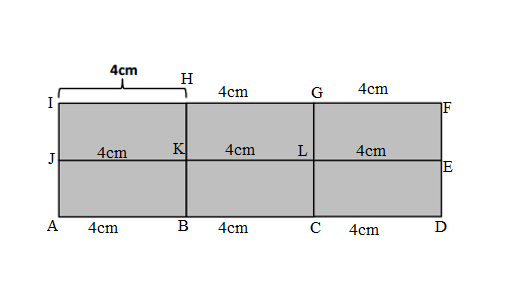
Area of the small rectangles = 12 square centimeters.
Length of the small rectangles = 4 centimeters
Width of the small rectangles = ??
Area of the small rectangles = Length × Width
=> 12 square centimeters = 4cm × Width
=> 12 square centimeters ÷ 4cm= Width
=> 3cm = Width.
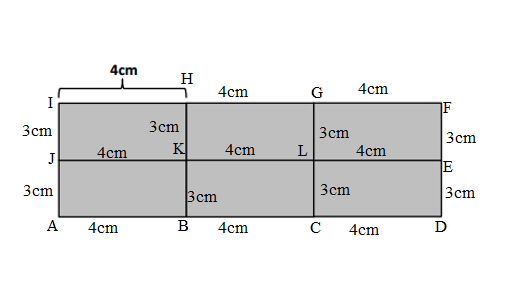
Length of the AD Side of the ADFI Daryl’s new rectangle = AB + BC + CD = 4cm + 4cm + 4cm = 8cm + 4cm = 12cm.
Width of the DF side of the ADFI Daryl’s new rectangle = ED + EF = 3cm + 3cm = 6cm.
Perimeter of the ADFI Daryl’s new rectangle = 2 ( Length + Width )
= 2 ( 12cm + 6cm )
= 2 × 18cm
= 36cm.
b. Length of the AD Side of the ADFI Daryl’s new rectangle = AB + BC + CD = 4cm + 4cm + 4cm = 8cm + 4cm = 12cm.
Width of the DF side of the ADFI Daryl’s new rectangle = ED + EF = 3cm + 3cm = 6cm.
Area of the ADFI Daryl’s new rectangle = Length × Width
= 12cm × 6cm
= 72 square cm
Question 3.
The recreation center soccer field measures 35 yards by 65 yards. Chris dribbles the soccer ball around the perimeter of the field 4 times. What is the total number of yards Chris dribbles the ball?
Answer:
Total number of yards Chris dribbles the ball = 800 yards.
Explanation:
Length of the recreation center soccer field = 65 yards
Width of the recreation center soccer field = 35 yards
Perimeter of the recreation center soccer field = 2 ( Length + Width )
= 2 ( 65 yards + 35 yards )
= 2 × 100 yards
= 200 yards.
Chris dribbles the soccer ball around the perimeter of the field 4 times.
Total number of yards Chris dribbles the ball = Perimeter of the recreation center soccer field × 4
= 200 yards × 4
= 800 yards.