Engage NY Eureka Math 3rd Grade Module 5 Lesson 27 Answer Key
Eureka Math Grade 3 Module 5 Lesson 27 Sprint Answer Key
A
Subtract by Seven




Question 1.
17 – 7 =
Answer :
17 – 7 = 10
Question 2.
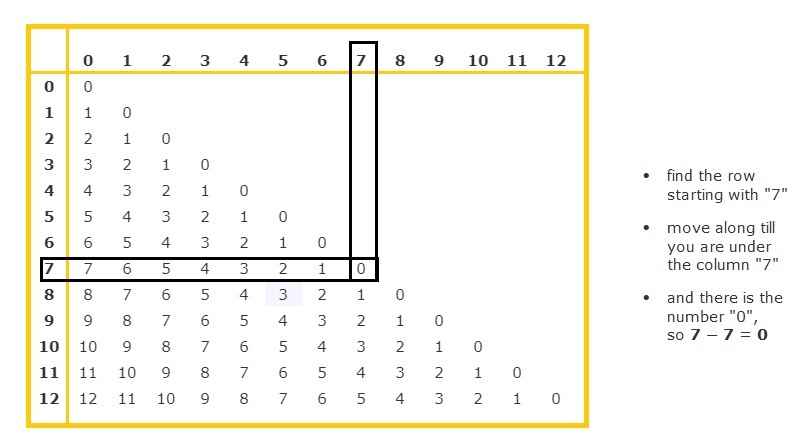
7 – 7 =
Answer :
7 – 7 = 0
Explanation :
Question 3.
27 – 7 =
Answer :
27 – 7 = 20
Question 4.
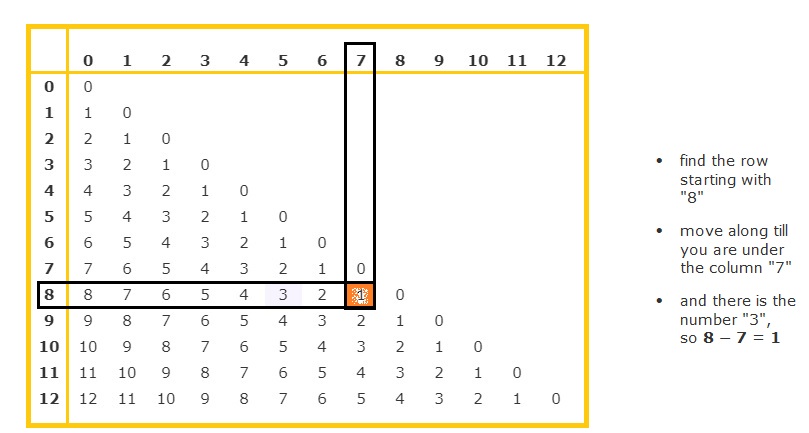
8 – 7 =
Answer :
8 – 7 = 1
Explanation :
Question 5.
18 – 7 =
Answer :
18 – 7 = 11
Question 6.
38 – 7 =
Answer :
38 – 7 = 31
Question 7.
9 – 7 =
Answer :
9 – 7 = 2
Question 8.
19 – 7 =
Answer :
19 – 7 = 2
Question 9.
49 – 7 =
Answer :
49 – 7 = 42
Question 10.
10 – 7 =
Answer :
10 – 7 = 3
Question 11.
20 – 7 =
Answer :
20 – 7 =13
Question 12.
60 – 7 =
Answer :
60 – 7 =53
Question 13.
11 – 7 =
Answer :
11 – 7 = 4
Question 14.
21 – 7 =
Answer :
21 – 7 = 14
Question 15.
71 – 7 =
Answer :
71 – 7 = 64
Question 16.
12 – 7 =
Answer :
12 – 7 = 5
Question 17.
22 – 7 =
Answer :
22 – 7 = 15
Question 18.
82 – 7 =
Answer :
82 – 7 = 75
Question 19.
13 – 7 =
Answer :
13 – 7 = 6
Question 20.
23 – 7 =
Answer :
23 – 7 = 16
Question 21.
83 – 7 =
Answer :
83 – 7 = 76
Question 22.
14 – 7 =
Answer :
14 – 7 = 7
Question 23.
24 – 7 =
Answer :
24 – 7 = 17
Question 24.
34 – 7 =
Answer :
34 – 7 = 27
Question 25.
64 – 7 =
Answer :
64 – 7 = 57
Question 26.
84 – 7 =
Answer :
84 – 7 = 77
Question 27.
15 – 7 =
Answer :
15 – 7 = 8
Question 28.
25 – 7 =
Answer :
25 – 7 = 18
Question 29.
35 – 7 =
Answer :
35 – 7 = 28
Question 30.
75 – 7 =
Answer :
75 – 7 = 68
Question 31.
55 – 7 =
Answer :
55 – 7 = 48
Question 32.
16 – 7 =
Answer :
16 – 7 = 9
Question 33.
26 – 7 =
Answer :
26 – 7 = 19
Question 34.
36 – 7 =
Answer :
36 – 7 = 29
Question 35.
86 – 7 =
Answer :
86 – 7 = 79
Question 36.
66 – 7 =
Answer :
66 – 7 = 59
Question 37.
90 – 7 =
Answer :
90 – 7 = 83
Question 38.
53 – 7 =
Answer :
53 – 7 = 46
Question 39.
42 – 7 =
Answer :
42 – 7 = 35
Question 40.
71 – 7 =
Answer :
71 – 7 = 64
Question 41.
74 – 7 =
Answer :
74 – 7 = 67
Question 42.
56 – 7 =
Answer :
56 – 7 = 49
Question 43.
95 – 7 =
Answer :
95 – 7 = 88
Question 44.
92 – 7 =
Answer :
92 – 7 = 85
B
Subtract by Seven

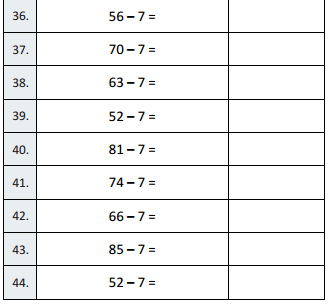
Question 1.
7 – 7 =
Answer :
7 – 7 = 0
Question 2.
17 – 7 =
Answer :
17 – 7 = 10
Question 3.
27 – 7 =
Answer :
27 – 7 = 20
Question 4.
8 – 7 =
Answer :
8 – 7 = 1
Question 5.
18 – 7 =
Answer :
18 – 7 = 9
Question 6.
68 – 7 =
Answer :
68 – 7 = 61
Question 7.
9 – 7 =
Answer :
9 – 7 = 2
Question 8.
19 – 7 =
Answer :
19 – 7 = 12
Question 9.
79 – 7 =
Answer :
79 – 7 = 72
Question 10.
10 – 7 =
Answer :
10 – 7 = 3
Question 11.
20 – 7 =
Answer :
20 – 7 = 13
Question 12.
90 – 7 =
Answer :
90 – 7 = 83
Question 13.
11 – 7 =
Answer :
11 – 7 = 4
Question 14.
21 – 7 =
Answer :
21 – 7 = 14
Question 15.
91 – 7 =
Answer :
91 – 7 = 84
Question 16.
12 – 7 =
Answer :
12 – 7 = 5
Question 17.
22 – 7 =
Answer :
22 – 7 = 15
Question 18.
42 – 7 =
Answer :
42 – 7 = 35
Question 19.
13 – 7 =
Answer :
13 – 7 = 6
Question 20.
23 – 7 =
Answer :
23 – 7 = 16
Question 21.
43 – 7 =
Answer :
43 – 7 = 36
Question 22.
14 – 7 =
Answer :
14 – 7 = 7
Question 23.
24 – 7 =
Answer :
24 – 7 = 17
Question 24.
34 – 7 =
Answer :
34 – 7 = 24
Question 25.
54 – 7 =
Answer :
54 – 7 = 47
Question 26.
74 – 7 =
Answer :
74 – 7 = 67
Question 27.
15 – 7 =
Answer :
15 – 7 = 8
Question 28.
25 – 7 =
Answer :
25 – 7 = 18
Question 29.
35 – 7 =
Answer :
35 – 7 = 28
Question 30.
65 – 7 =
Answer :
65 – 7 = 58
Question 31.
45 – 7 =
Answer :
45 – 7 = 38
Question 32.
16 – 7 =
Answer :
16 – 7 = 9
Question 33.
26 – 7 =
Answer :
26 – 7 = 19
Question 34.
36 – 7 =
Answer :
36 – 7 = 29
Question 35.
76 – 7 =
Answer :
76 – 7 = 69
Question 36.
56 – 7 =
Answer :
56 – 7 = 49
Question 37.
70 – 7 =
Answer :
70 – 7 = 63
Question 38.
63 – 7 =
Answer :
63 – 7 = 56
Question 39.
52 – 7 =
Answer :
52 – 7 = 45
Question 40.
81 – 7 =
Answer :
81 – 7 = 74
Question 41.
74 – 7 =
Answer :
74 – 7 = 67
Question 42.
66 – 7 =
Answer :
66 – 7 = 59
Question 43.
85 – 7 =
Answer :
85 – 7 = 78
Question 44.
52 – 7 =
Answer :
52 – 7 = 45
Eureka Math Grade 3 Module 5 Lesson 27 Problem Set Answer Key
Question 1.
Use the pictures to model equivalent fractions. Fill in the blanks, and answer the questions.
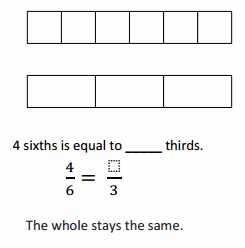
What happened to the size of the equal parts when there were fewer equal parts?
What happened to the number of equal parts when the equal parts became larger?
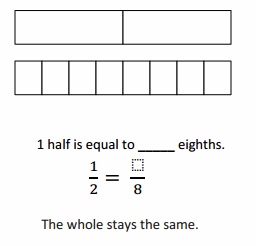
What happened to the size of the equal parts when there were more equal parts?
What happened to the number of equal parts when the equal parts became smaller?
Answer :
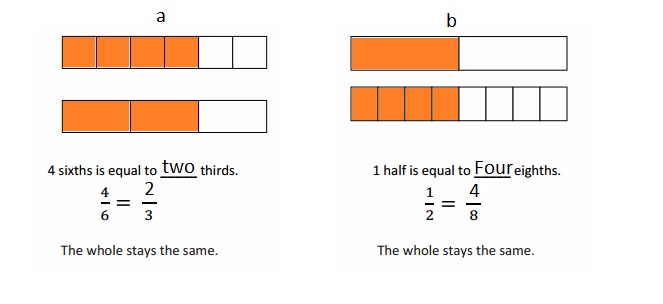
Explanation :
In figure a
When there are fewer parts the size of the equal parts are bigger .
When the equal parts became larger The number of equal parts will become fewer .
In figure b
when there were more equal parts the size of the equal parts are smaller .
when the equal parts became smaller the number of equal parts will become more .
Question 2.
6 friends want to share 3 chocolate bars that are all the same size, which are represented by the 3 rectangles below. When the bars are unwrapped, the friends notice that the first chocolate bar is cut into 2 equal parts, the second is cut into 4 equal parts, and the third is cut into 6 equal parts. How can the 6 friends share the chocolate bars equally without breaking any of the pieces?

Answer :
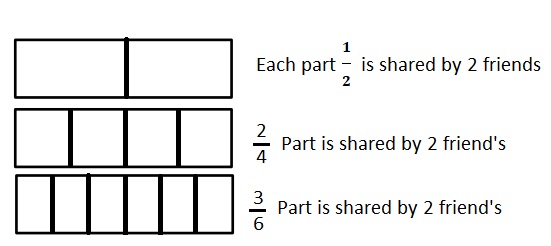
Explanation :
The First Chocolate is shared by 2 friend’s with \(\frac{1}{2}\) part each .
The Second chocolate is shared by 2 friend’s with\(\frac{2}{4}\) part each .
The Third chocolate is shared by 2 friend’s with\(\frac{3}{6}\) part each .
That means each friend will get \(\frac{1}{2}\) of one chocolate .
Question 3.
When the whole is the same, why does it take 6 copies of 1 eighth to equal 3 copies of 1 fourth? Draw a model to support your answer.
Answer :

Explanation :
It takes Six one-Eighths to make Three one Fourths.
\(\frac{3}{4}\) is equivalent to \(\frac{6}{8}\) .
Question 4.
When the whole is the same, how many sixths does it take to equal 1 third? Draw a model to support your answer.
Answer :
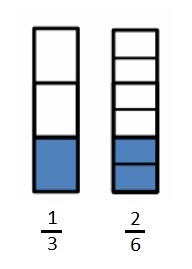
Explanation :
It takes two one-sixths to make a third. and we can see that there are \(\frac{1}{6}\) = 6 sixths in a whole.
Question 5.
You have a magic wand that doubles the number of equal parts but keeps the whole the same size. Use your magic wand. In the space below, draw to show what happens to a rectangle that is partitioned in fourths after you tap it with your wand. Use words and numbers to explain what happened.

Answer :
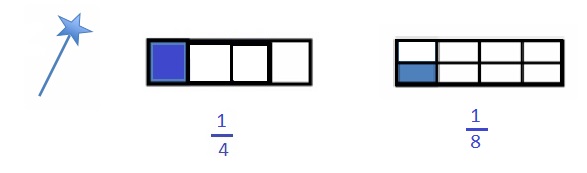
Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in Fourths. after magic the Rectangular strip is partitioned into eigths with same length by dividing the rectangular strip in middle as shown in above figure .
Eureka Math Grade 3 Module 5 Lesson 27 Exit Ticket Answer Key
Question 1.
Solve.
2 thirds is equal to __ twelfths
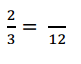
Answer :
2 thirds is equal to 8 twelfths
Question 2.
Draw and label two models that show fractions equivalent to those in Problem 1.
Answer :
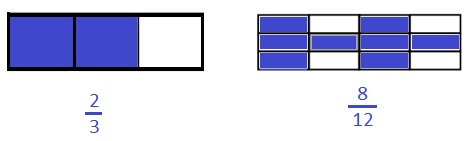
Explanation :
2 thirds is equal to 8 twelfths
Question 3.
Use words to explain why the two fractions in Problem 1 are equal.
Answer :
Both the wholes have same length .
The Rectangular strip is partitioned in Thirds. The Same Rectangular strip is partitioned into twelfths with same length by dividing the rectangular strip in middle into by 2 strips as shown in above figure .
Eureka Math Grade 3 Module 5 Lesson 27 Homework Answer Key
Question 1.
Use the pictures to model equivalent fractions. Fill in the blanks, and answer the questions.
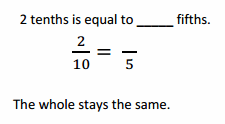
What happened to the size of the equal parts when there were fewer equal parts?
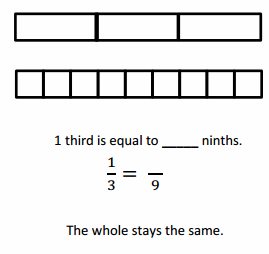
What happened to the size of the equal parts when there were more equal parts?
Answer :
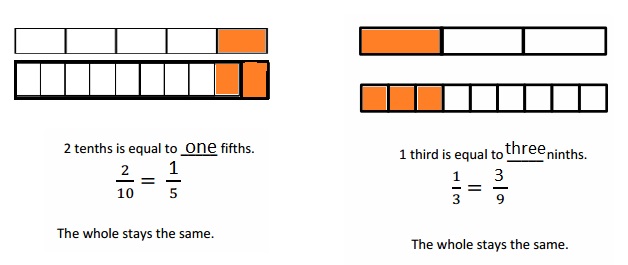
Explanation :
when there were fewer equal parts the number of parts are bigger .
when there were more equal parts the number of parts are smaller .
Question 2.
8 students share 2 pizzas that are the same size, which are represented by the 2 circles below. They notice that the first pizza is cut into 4 equal slices, and the second is cut into 8 equal slices. How can the 8 students share the pizzas equally without cutting any of the pieces?
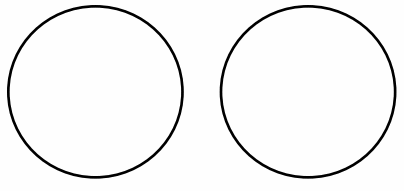
Answer :
Explanation :
Each student gets \(\frac{1}{4}\) or \(\frac{2}{8}\) of the pizza . From 1 st pizza 4 students get \(\frac{1}{4}\) of the pizza and from 2nd pizza 4 students get \(\frac{2}{8}\) of the pizza .
Question 3.
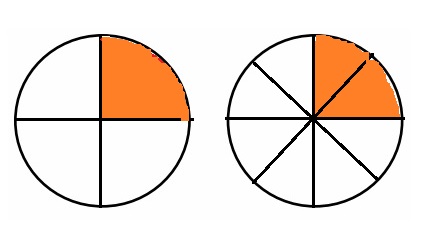
When the whole is the same, why does it take 4 copies of 1 tenth to equal 2 copies of 1 fifth? Draw a model to support your answer.
Answer :
Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in fifths. The Another Rectangular strip is partitioned into tenths with same length by dividing the rectangular strip in middle as shown in above figure .
two one fifths is equal to four one tenths .
Question 4.
When the whole is the same, how many eighths does it take to equal 1 fourth? Draw a model to support your Answer.
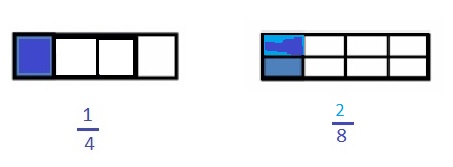
Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in fourths. The Another Rectangular strip is partitioned into Eigths with same length by dividing the rectangular strip in middle as shown in above figure .
one fourths is equal to four two Eighths .
Question 5.
Mr. Pham cuts a cake into 8 equal slices. Then, he cuts every slice in half. How many of the smaller slices does he have? Use words and numbers to explain your answer.
Answer :
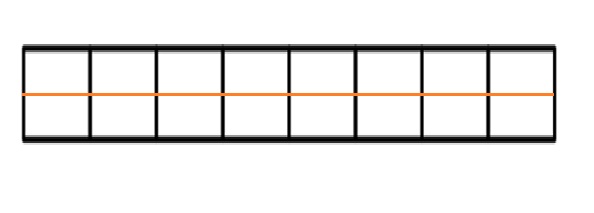
Explanation :
The figure shows a cake of 8 slices .the middle orange line shows the cake is sliced in half , creating 16 small slices .