Eureka Math Geometry Module 5 Lesson 9 Answer Key

Engage NY Eureka Math Geometry Module 5 Lesson 9 Answer Key

Eureka Math Geometry Module 5 Lesson 9 Example Answer Key

Example 1.
a. What is the length of the arc that measures 60° in a circle of radius 10 cm?

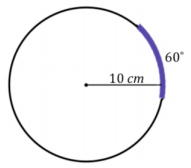
Answer:
Arc length = \(\frac{1}{6}\) (2π×10)
Arc length = \(\frac{10 \pi}{3}\)
The marked arc length is \(\frac{10 \pi}{3}\) cm.

b. Given the concentric circles with center A and with m∠A = 60°, calculate the arc length intercepted by ∠A on each circle. The inner circle has a radius of 10, and each circle has a radius 10 units greater than the previous circle.

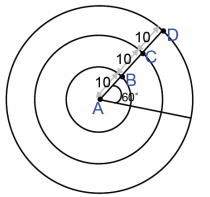
Answer:
Arc length of circle with radius \(\overline{A B}\) = (\(\frac{60}{360}\))(2π)(10) = \(\frac{10 \pi}{3}\)
Arc length of circle with radius \(\overline{A C}\) = (\(\frac{60}{360}\))(2π)(20) = \(\frac{20 \pi}{3}\)
Arc length of circle with radius \(\overline{A D}\) = (\(\frac{60}{360}\))(2π)(30) = \(\frac{30 \pi}{3}\) = 10π

c. An arc, again of degree measure 60°, has an arc length of 5π cm. What is the radius of the circle on which the arc sits?
Answer:
\(\frac{1}{6}\) (2π×r) = 5π
2πr = 30π
r = 15
The radius of the circle on which the arc sits is 15 cm.

d. Give a general formula for the length of an arc of degree measure x° on a circle of radius r.
Answer:
Arc length = (\(\frac{x}{360}\))2πr

e. Is the length of an arc intercepted by an angle proportional to the radius? Explain.
Answer:
Yes, the arc length is a constant \(\frac{2 \pi x}{360}\) times the radius when x is a constant angle measure, so it is proportional to the radius of an arc intercepted by an angle.

SECTOR: Let \(\widehat{A B}\) be an arc of a circle with center O and radius r. The union of all segments \(\overline{O P}\), where P is any point of \(\widehat{A B}\), is called a sector.

Answer:
→ We can use the constant of proportionality \(\frac{\pi}{180}\) to define a new angle measure, a radian. A radian is the measure of the central angle of a sector of a circle with arc length of one radius length. Say that with me.
→ A radian is the measure of the central angle of a sector of a circle with arc length of one radius length.
→ So, 1° = \(\frac{\pi}{180}\) radians. What does 180° equal in radian measure?
π radians
→ What does 360° or a rotation through a full circle equal in radian measure?
2π radians
→ Notice, this is consistent with what we found above. You will learn more about radian measure and why it was developed in Algebra II and Calculus.

Example 2.
a. Circle O has a radius of 10 cm. What is the area of the circle? Write the formula.
Answer:
Area = π(10 cm)² = 100π cm²

b. What is the area of half of the circle? Write and explain the formula.
Answer:
Area = \(\frac{1}{2}\) (π(10 cm)²) = 50π cm². 10 cm is the radius of the circle, and \(\frac{1}{2}\) = \(\frac{180}{360}\), which is the fraction of the circle.

c. What is the area of a quarter of the circle? Write and explain the formula.
Answer:
Area = \(\frac{1}{4}\) (π(10 cm)²) = 25π cm². 10 cm is the radius of the circle, and \(\frac{1}{4}\) = \(\frac{90}{360}\), which is the fraction of the circle.

d. Make a conjecture about how to determine the area of a sector defined by an arc measuring 60°.
Answer:
Area(sector AOB) = \(\frac{60}{360}\) (π(10 cm)²) = \(\frac{1}{6}\) (π(10 cm)²); the area of the circle times the arc measure divided by 360
Area(sector AOB) = \(\frac{50\pi}{3}\) cm²
The area of the sector AOB is \(\frac{50\pi}{3}\) cm².

e. Circle O has a minor arc \(\widehat{A C}\) with an angle measure of 60°. Sector AOB has an area of 24π. What is the radius of circle O?
Answer:
24π = \(\frac{1}{6}\) (πr²)
144π = (πr²)
r = 12
The radius has a length of 12 units.

f. Give a general formula for the area of a sector defined by an arc of angle measure x° on a circle of radius r.
Answer:
Area of sector = (\(\frac{x}{360}\))πr²

Eureka Math Geometry Module 5 Lesson 9 Exercise Answer Key

Exercise 1.
The radius of the following circle is 36 cm, and the m∠ABC = 60°.

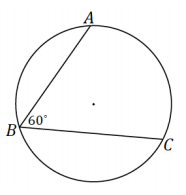
a. What is the arc length of \(\widehat{A C}\)?
The degree measure of \(\widehat{A C}\) is 120°. Then the arc length of \(\widehat{A C}\) is calculated by
Arc length = \(\frac{1}{3}\) (2π ∙ 36)
Arc length = 24π.
The arc length of \(\widehat{A C}\) is 24π cm.

b. What is the radian measure of the central angle?
Answer:
Arc length = (angle measure of central angle in radians)(radius)
Arc length = (angle measure of central angle in radians)(36)
24π = 36(angle measure of central angle in radians)
(angle measure of central angle in radians) = \(\frac{24\pi}{36}\) = \(\frac{2\pi}{3}\)
The measure of the central angle is \(\frac{2\pi}{3}\) radians.

Exercises 2–3
Exercise 2.
The area of sector AOB in the following image is 28π cm². Find the measurement of the central angle labeled x°.

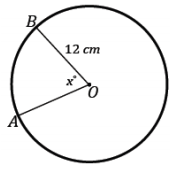
Answer:
28π = \(\frac{x}{360}\) (π(12)² )
x = 70
The central angle has a measurement of 70°.

Exercise 3.
In the following figure of circle O, m∠AOC = 108° and \(\widehat{A B}\) = \(\widehat{A C}\) = 10 cm.

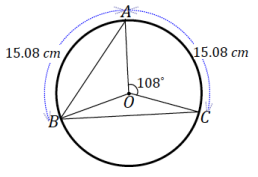
a. Find m∠OAB.
Answer:
36°

b. Find \(m\widehat{B C}\).
Answer:
144°

c. Find the area of sector BOC.
Answer:
Area(sector BOC) = \(\frac{144}{360}\) (π(5.305)²)
Area(sector BOC) ≈ 35.37
The area of sector BOC is 35.37 cm².

Eureka Math Geometry Module 5 Lesson 9 Problem Set Answer Key

Question 1.
P and Q are points on the circle of radius 5 cm, and the measure of \(\widehat{P Q}\) is 72°. Find, to one decimal place, each of the following.

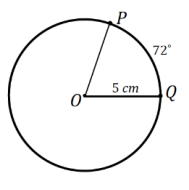
a. The length of \(\widehat{P Q}\)
Answer:
Arc length(\(\widehat{P Q}\)) = \(\frac{72}{360}\) (2π×5)
Arc length(\(\widehat{P Q}\)) = 2π
The arc length of \(\widehat{P Q}\) is 2π cm or approximately 6.3 cm.

b. The ratio of the arc length to the radius of the circle
Answer:
\(\frac{\pi}{180}\) ∙ 72 = \(\frac{2\pi}{5}\) radians

c. The length of chord \(\overline{P Q}\)
Answer:

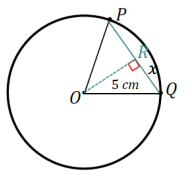
The length of \(\overline{P Q}\) is twice the value of x in △OQR.
x = 5 sin⁡36°
PQ = 2x = 10 sin⁡36°
Chord \(\overline{P Q}\) has a length of 10 sin⁡36 cm or approximately 5.9 cm.

d. The distance of the chord \(\overline{P Q}\) from the center of the circle
Answer:

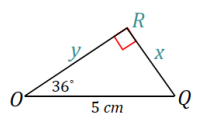
The distance of chord \(\overline{P Q}\) from the center of the circle is labeled as y in △OQR.
y = 5 cos⁡36°
The distance of chord \(\overline{P Q}\) from the center of the circle is 5 cos⁡36 cm, or approximately 4 cm.

e. The perimeter of sector POQ
Answer:
Perimeter(sector POQ) = 5 + 5 + 2π
Perimeter(sector POQ) = 10 + 2π
The perimeter of sector POQ is (10 + 2π) cm, or approximately 16.3 cm.

f. The area of the wedge between the chord \(\overline{P Q}\)and \(\widehat{P Q}\)
Answer:
Area(wedge) = Area(sector POQ) – Area(△POQ)
Area(△POQ) = \(\frac{1}{2}\) (10 sin⁡36 )(5 cos⁡36 )
Area(sector POR) = \(\frac{72}{360}\) (π(5)²)
Area(wedge) = \(\frac{72}{360}\) (π(5)² ) – \(\frac{1}{2}\) (10 sin⁡36 )(5 cos⁡36 )
The area of wedge between chord \(\overline{P Q}\)and the arc PQ is approximately 3.8 cm².

g. The perimeter of this wedge
Answer:
Perimeter(wedge) = 2π + 10 sin⁡36
The perimeter of the wedge is approximately 12.2 cm.

Question 2.
What is the radius of a circle if the length of a 45° arc is 9π?
Answer:
9π = \(\frac{45}{360}\) (2πr)
r = 36
The radius of the circle is 36.

Question 3.
\(\widehat{A B}\) and \(\widehat{C D}\) both have an angle measure of 30°, but their arc lengths are not the same. OB = 4 and BD = 2.

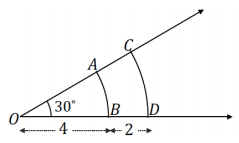
a. What are the arc lengths of \(\widehat{A B}\) and \(\widehat{C D}\)?
Arc length(\(\widehat{A B}\) ) = \(\frac{30}{360}\) (2π)(4)
Arc length(\(\widehat{A B}\) ) = \(\frac{2}{3}\) π
The arc length of \(\widehat{A B}\) is \(\frac{2}{3}\) π.
Arc length(\(\widehat{C D}\) ) = \(\frac{30}{360}\) (2π)(6)
Arc length(\(\widehat{C D}\) ) = π
The arc length of \(\widehat{C D}\) is π.

b. What is the ratio of the arc length to the radius for both of these arcs? Explain.
Answer:
\(\frac{30\pi}{180}\) = \(\frac{\pi}{6}\) radians. The angle is constant, so the ratio of arc length to radius will be the angle measure, 30°, multiplied by \(\frac{\pi}{180}\).

c. What are the areas of the sectors AOB and COD?
Answer:
Area(sector AOB) = \(\frac{30}{360}\) (π(4)²)
Area(sector AOB) = \(\frac{4}{3}\) π
The area of the sector AOB is \(\frac{4}{3}\) π.
Area(sector COD) = \(\frac{30}{360}\) (π(6)²)
The area of the sector COD is 3π.

Question 4.
In the circles shown, find the value of x. Figures are not drawn to scale.
a. The circles have central angles of equal measure.

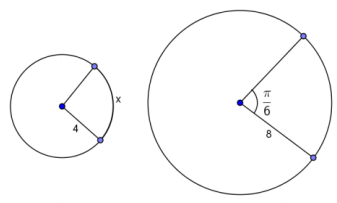
Answer:
x = (4)(\(\frac{\pi}{6}\)) = \(\frac{2\pi}{3}\)
\(\frac{2\pi}{3}\) radians

b.

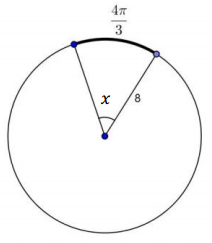
Answer:
x = \(\frac{\pi}{6}\)
\(\frac{\pi}{6}\) radians

c.

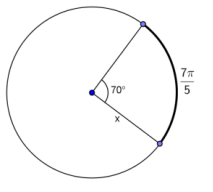
Answer:
x = \(\frac{18}{5}\)

d.

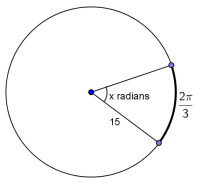
Answer:
x = \(\frac{2\pi}{45}\)

Question 5.
The concentric circles all have center A. The measure of the central angle is 45°. The arc lengths are given.

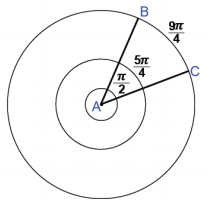
a. Find the radius of each circle.
Answer:
Radius of inner circle: \(\frac{\pi}{2}\) = \(\frac{45\pi}{180}\) r, r = 2
Radius of middle circle: \(\frac{5\pi}{4}\) = \(\frac{45\pi}{180}\) r, r = 5
Radius of outer circle: \(\frac{9\pi}{4}\) = \(\frac{45\pi}{180}\) r, r = 9

b. Determine the ratio of the arc length to the radius of each circle, and interpret its meaning.
Answer:
\(\frac{\pi}{4}\) is the ratio of the arc length to the radius of each circle. It is the measure of the central angle in radians.

Question 6.
In the figure, if the length of \(\widehat{P Q}\) is 10 cm, find the length of \(\widehat{Q R}\).

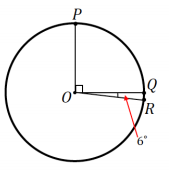
Answer:
Since 6° is \(\frac{1}{15}\) of 90°, then the arc length of \(\widehat{Q R}\) is \(\frac{1}{15}\) of 10 cm; the arc length of \(\widehat{Q R}\) is \(\frac{2}{3}\) cm.

Question 7.
Find, to one decimal place, the areas of the shaded regions.
a.

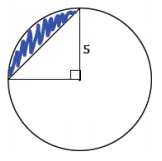
Answer:
Shaded Area = Area of sector – Area of Triangle
(or \(\frac{1}{4}\) (Area of circle) – Area of triangle)
Shaded Area = \(\frac{90}{360}\) (π(5)² ) – \(\frac{1}{2}\)(5)(5)
Shaded Area = 6.25π – 12.5

The shaded area is approximately 7.13.

b. The following circle has a radius of 2.

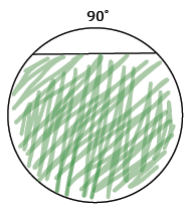
Answer:

Shaded Area = \(\frac{3}{4}\) (Area of circle) + Area of triangle
Note: The triangle is a 45° – 45° – 95° triangle with legs of length 2 (the legs are comprised by the radii, like the triangle in the previous question).
Shaded Area = \(\frac{3}{4}\) (π(2)² ) + \(\frac{1}{2}\)(2)(2)
Shaded Area = 3π + 2
The shaded area is approximately 11.4.

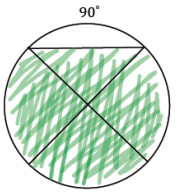
c.

Answer:

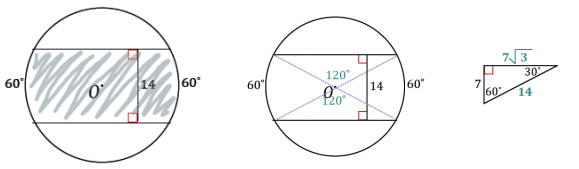
Shaded Area = (Area of 2 sectors) + (Area of 2 triangles)
Shaded Area = 2(\(\frac{98}{3}\) π) + 4(\(\frac{49 \sqrt{3}}{2}\))
Shaded Area = \(\frac{196}{3}\) π + 98\(\sqrt{3}\)
The shaded area is approximately 374.99.

Eureka Math Geometry Module 5 Lesson 9 Exit Ticket Answer Key

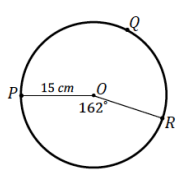
Question 1.
Find the arc length of \(\widehat{P Q R}\).
Answer:
Arc length(\(\widehat{P R}\)) = \(\frac{162}{360}\) (2π)(15)
Arc length(\(\widehat{P R}\)) = 13.5π
Circumference(circle O) = 30π
The arc length of \(\widehat{P Q R}\) is (30π – 13.5π) cm or 16.5π cm.

Question 2.
Find the area of sector POR.
Answer:
Area(sector POR) = \(\frac{162}{360}\) (π(15)² )
Area(sector POR) = 101.25π
The area of sector POR is 101.25π cm².