Eureka Math Geometry Module 5 Lesson 6 Answer Key

Engage NY Eureka Math Geometry Module 5 Lesson 6 Answer Key

Eureka Math Geometry Module 5 Lesson 6 Exercise Answer Key

Opening Exercise
In a circle, a chord \(\overline{D E}\) and a diameter \(\overline{A B}\) are extended outside of the circle to meet at point C. If m∠DAE = 46°, and m∠DCA = 32°, find m∠DEA.

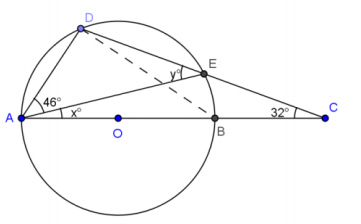
Let m∠DEA = y˚, m∠EAB = x˚

In △ABD, m∠DBA =
Reason:
Answer:
In △ABD, m∠DBA = y˚
Reason: angles inscribed in same arc are congruent

m∠ADB =
Reason:
Answer:
m∠ADB = 90° Reason: angle inscribed in semicircle

∴46 + x + y + 90 =
Reason:
Answer:
∴46 + x + y + 90 = 180 Reason: sum of angles of triangle is 180°

x + y =
Answer:
x + y = 44

In △ACE, y = x + 32
Reason:
Answer:
In △ACE, y = x + 32
Reason: Exterior angle of a triangle is equal to the sum of the remote interior angles

x + x + 32 =
Reason:
Answer:
x + x + 32 = 44
Reason: substitution

x =
Answer:
x = 6

y =
Answer:
y = 38

m∠DEA =
Answer:
m∠DEA = 38°

Exercises
Find the value of x in each figure below, and describe how you arrived at the answer.

Exercise 1.
Hint: Thales’ theorem

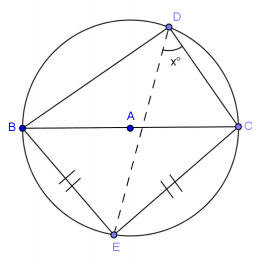
Answer:
m∠BEC = 90° inscribed in a semicircle
m∠EBC = m∠ECB = 45° base angles of an isosceles triangle are congruent and sum of angles of a triangle = 180°
m∠EBC = m∠EDC = 45° angles inscribed in the same arc are congruent
x = 45

Exercise 2.

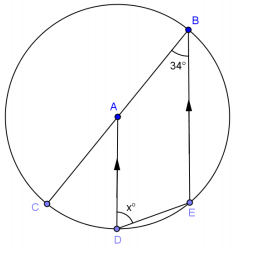
Answer:
m∠BAD = 146˚, if parallel lines cut by a transversal, then interior angles on the same side are supplementary. Then the \(m \widehat{B D}\) = 146˚, because ∠BAD is a central angle intercepting \(\widehat{B D}\). Then remaining arc of the circle, \(\widehat{B C D}\), has a measure of 214°. Then m∠BED = 107˚ since it is an inscribed angle intercepting \(\widehat{B C D}\). The angle sum of a quadrilateral is 360°, which means x = 73.

Exercise 3.

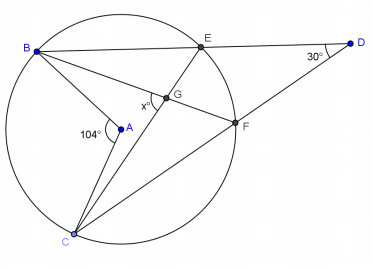
Answer:
m∠BEC = m∠CFB = \(\frac{1}{2}\) m∠BAC = 52°
Inscribed angles are half the measure of the central angle intercepting the same arc.
m∠DEG = 128° linear pair with ∠BEC
m∠GFD = 128° linear pair with ∠CFB
m∠EGF = 74° sum of angles of a quadrilateral
x = 74 vertical angles

Exercise 4.

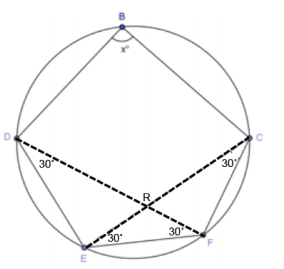
Answer:
The measures of arcs \(\widehat{D E}\), \(\widehat{E F}\), and \(\widehat{F C}\) are each 60˚, since the intercepted arc of an inscribed angle is double the measure of the angle. This means \(\widehat{m D E} C\) = 180˚, or \(\widehat{D E C}\) is a semicircle. This means x is 90, since ∠DBC is inscribed in a semicircle.

Eureka Math Geometry Module 5 Lesson 6 Problem Set Answer Key

In Problems 1–5, find the value x.
Question 1.

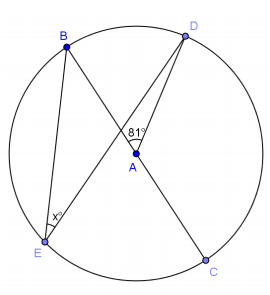
Answer:
x = 40.5

Question 2.

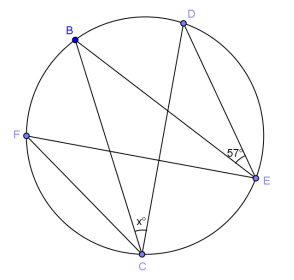
Answer:
x = 57

Question 3.

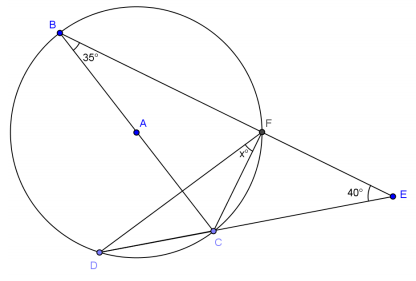
Answer:
x = 15

Question 4.

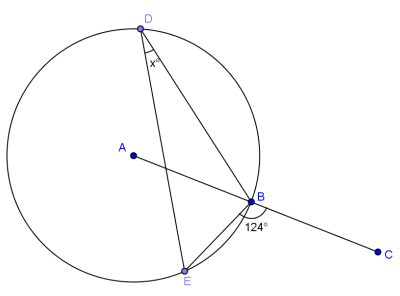
Answer:
x = 34

Question 5.

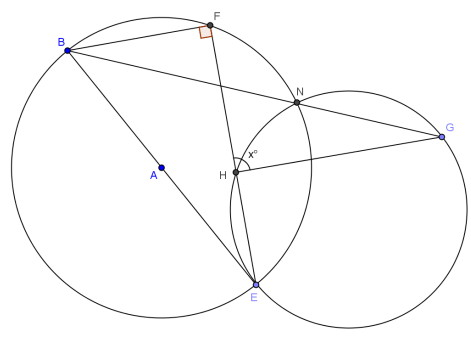
Answer:
x = 90

Question 6.
If BF = FC, express y in terms of x.

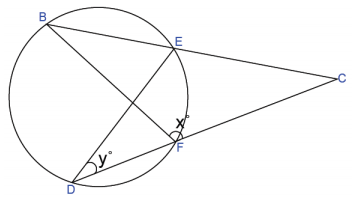
Answer:
y = 90 – \(\frac{x}{2}\)

Question 7.
a. Find the value of x.

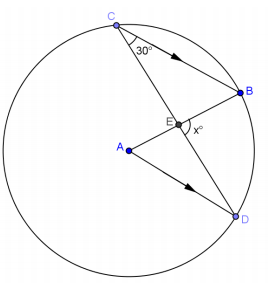
Answer:
x = 90

b. Suppose the m∠C = a°. Prove that m∠DEB = 3a°.
Answer:
m∠D = a° (alternate angles are equal in measure), m∠A = 2a° (inscribed angles half the central angle), a° + 2a° + m∠AED = 180° (the sum of the angles of triangle is 180°), m∠AED = (180 – 3a)°, m∠AED + m∠DEB = 180° (angles form line), (180 – 3a)° + m∠DEB = 180° (substitution), m∠DEB = 3a°

Question 8.
In the figure below, three identical circles meet at B, F, C, and E, respectively. BF = CE. A, B, C and F, E, D lie on straight lines.
Prove ACDF is a parallelogram.

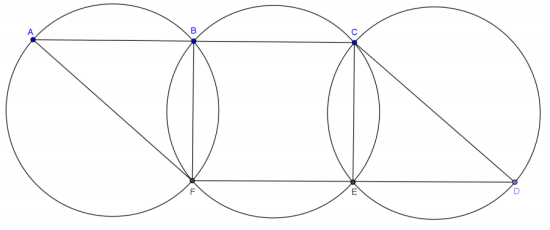
PROOF:

Join BE and CF.
BF = CE Reason: ______________________________
a = __________ = __________ = __________ = d Reason: ______________________________
__________ = __________ Alternate interior angles are equal in measure.
\(\overline{A C}\) ∥ \(\overline{F D}\)
__________ = __________ Corresponding angles are equal in measure.
\(\overline{A F}\) ∥ \(\overline{B E}\)
__________ = __________ Corresponding angles are equal in measure.
\(\overline{B E}\) ∥ \(\overline{C D}\)
\(\overline{A F}\) ∥ \(\overline{B E}\)∥\(\overline{C D}\)
ACDF is a parallelogram.
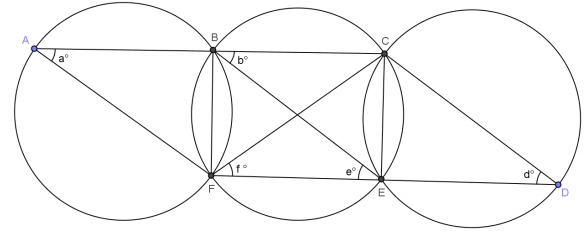
Answer:
Join BE and CF.
BF = CE       Reason: Given
a = b = f = e = d       Reason: Angles inscribed in congruent arcs are equal in
m∠CBE = m∠FEB       Alternate interior angles are equal in measure.
\(\overline{A C}\) ∥ \(\overline{F D}\)
m∠A = m∠CBE         Corresponding angles are equal in measure.
\(\overline{A F}\) ∥ \(\overline{B E}\)
m∠D = m∠BEF           Corresponding angles are equal in measure.
\(\overline{B E}\) ∥ \(\overline{C D}\)
\(\overline{A F}\) ∥ \(\overline{B E}\)∥\(\overline{C D}\)
ACDF is a parallelogram.

Eureka Math Geometry Module 5 Lesson 6 Exit Ticket Answer Key

Question 1.
Find the measure of angles x and y. Explain the relationships and theorems used.

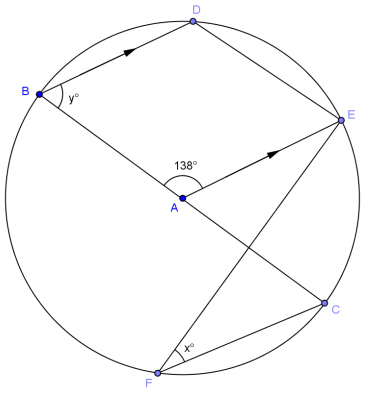
Answer:
m∠EAC = 42° (linear pair with ∠BAE). m∠EFC = \(\frac{1}{2}\) m∠EAC = 21° (inscribed angle is half measure of central angle with same intercepted arc). x = 21.
m∠ABD = m∠EAC = 42° (corresponding angles are equal in measure). y = 42.