Engage NY Eureka Math Geometry Module 5 Lesson 5 Answer Key
Eureka Math Geometry Module 5 Lesson 5 Example Answer Key
Example 1.
A and C are points on a circle with center O.
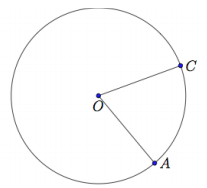
a. What is the intercepted arc of ∠COA? Color it red.
Answer:
\(\widehat{A C}\)
b. Draw triangle AOC. What type of triangle is it? Why?
Answer:
An isosceles triangle because OC = OA (they are radii of the same circle).
c. What can you conclude about m∠OCA and m∠OAC? Why?
Answer:
They are equal because base angles of an isosceles triangle are equal in measure.
d. Draw a point B on the circle so that O is in the interior of the inscribed angle ABC.
Answer:
The diagram should resemble the inside case of the discussion diagrams.
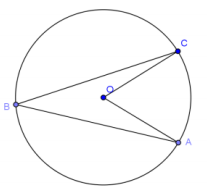
e. What is the intercepted arc of ∠ABC? Color it green.
Answer:
\(\widehat{A C}\)
f. What do you notice about \(\widehat{A C}\)?
Answer:
It is the same arc that was intercepted by the central angle.
g. Let the measure of ∠ABC be x and the measure of ∠AOC be y. Can you prove that y = 2x? (Hint: Draw the diameter that contains point B.)
Answer:
Let \(\overline{B D}\) be a diameter. Let x1, y1, x2, and y2 be the measures of ∠CBD, ∠COD, ∠ABD, and ∠AOD, respectively. We can express x and y in terms of these measures: x = x1 + x2, and y = y1 + y2. By the Opening Exercise, y1 = 2x1, and y2 = 2x2. Thus, y = 2x.
h. Does your conclusion support the inscribed angle theorem?
Answer:
Yes, even when the center of the circle is in the interior of the inscribed angle, the measure of the inscribed angle is equal to half the measure of the central angle that intercepts the same arc.
i. If we combine the Opening Exercise and this proof, have we finished proving the inscribed angle theorem?
Answer:
No. We still have to prove the case where the center is outside the inscribed angle.
Example 2.
A and C are points on a circle with center O.

a. Draw a point B on the circle so that O is in the exterior of the inscribed angle ABC.
Answer:
The diagram should resemble the outside case of the discussion diagrams.
b. What is the intercepted arc of ∠ABC? Color it yellow.
Answer:
\(\widehat{A C}\)
c. Let the measure of ∠ABC be x and the measure of ∠AOC be y. Can you prove that y = 2x? (Hint: Draw the diameter that contains point B.)
Answer:
Let \(\overline{B D}\) be a diameter. Let x1, y1, x2, and y2 be the measures of ∠CBD, ∠COD, ∠ABD, and ∠AOD, respectively. We can express x and y in terms of these measures: x = x2 – x1 and y = y2 – y1. By the Opening Exercise, y1 = 2x1 and y2 = 2x2. Thus, y = 2x.
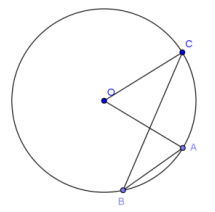
d. Does your conclusion support the inscribed angle theorem?
Answer:
Yes, even when the center of the circle is in the exterior of the inscribed angle, the measure of the inscribed angle is equal to half the measure of the central angle that intercepts the same arc.
e. Have we finished proving the inscribed angle theorem?
Answer:
We have shown all cases of the inscribed angle theorem (central angle version). We do have one more case to study in Lesson 7, but it is ok not to mention it here. The last case is when the location of B is on the minor arc between A and C.
Eureka Math Geometry Module 5 Lesson 5 Exercise Answer Key
Opening Exercise
a. A and C are points on a circle with center O.
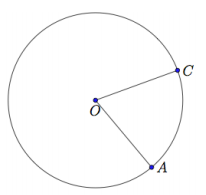
i. Draw a point B on the circle so that \(\overline{A B}\) is a diameter. Then draw the angle ABC.
ii. What angle in your diagram is an inscribed angle?
Answer:
∠ABC
iii. What angle in your diagram is a central angle?
Answer:
∠AOC
iv. What is the intercepted arc of ∠ABC?
Answer:
\(\widehat{A C}\)
v. What is the intercepted arc of ∠AOC ?
Answer:
\(\widehat{A C}\)
b. The measure of the inscribed angle ACD is x, and the measure of the central angle CAB is y. Find m∠CAB in terms of x.
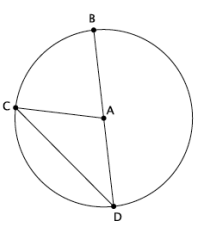
Answer:
We are given that m∠ACD is x. We know that AB = AC = AD, so △CAD is an isosceles triangle, which means that m∠ADC is also x. The sum of the angles of a triangle is 180˚, so m∠CAD = 180˚ – 2x. ∠CAD and ∠CAB are supplementary meaning that m∠CAB = 180˚ – (180˚ – 2x) = 2x; therefore, y = 2x.
Exercises
Exercise 1.
Find the measure of the angle with measure x. Diagrams are not drawn to scale.
a. m∠D = 25°
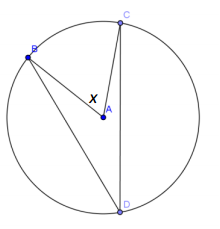
Answer:
50°
b. m∠D = 15°
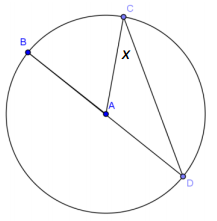
Answer:
15°
c. m∠BAC = 90°
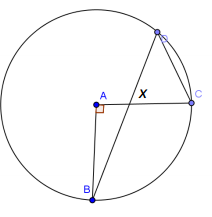
Answer:
45°
d. m∠B = 32°
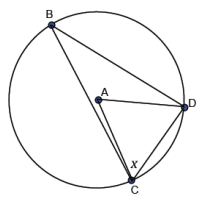
Answer:
58°
e. BD = AB
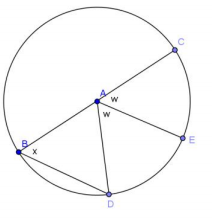
Answer:
x = w = 60°
f. m∠D = 19°
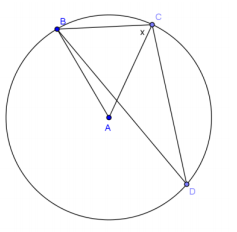
Answer:
71°
Exercise 2.
Toby says △BEA is a right triangle because m∠BEA = 90°. Is he correct? Justify your answer.
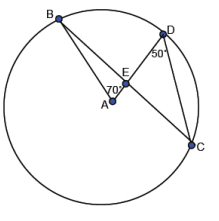
Answer:
Toby is not correct. m∠BEA = 95°. ∠BCD is inscribed in the same arc as the central angle, so it has a measure of 35°. This means that m∠DEC = 95° because the sum of the angles of a triangle is 180°. m∠BEA = m∠DEC since they are vertical angles, so the triangle is not right.
Exercise 3.
Let’s look at relationships between inscribed angles.
a. Examine the inscribed polygon below. Express x in terms of y and y in terms of x. Are the opposite angles in any quadrilateral inscribed in a circle supplementary? Explain.
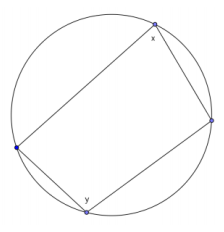
Answer:
x = 180˚ – y; y = 180˚ – x. The angles are supplementary.
b. Examine the diagram below. How many angles have the same measure, and what are their measures in terms of x˚?
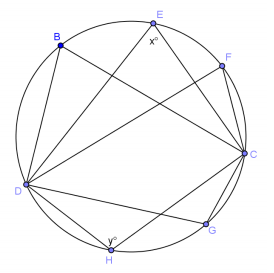
Answer:
Let C and D be the points on the circle that the original angles contain. All the angles intercepting the minor arc between C and D have measure x˚, and the angles intercepting the major arc between C and D measure 180° – x.
Exercise 4.
Find the measures of the labeled angles.
a.
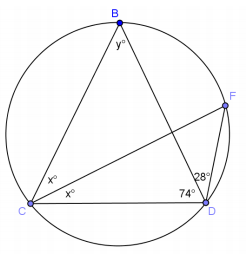
Answer:
x = 28, y = 50
b.
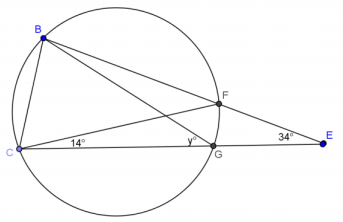
Answer:
y = 48
c.
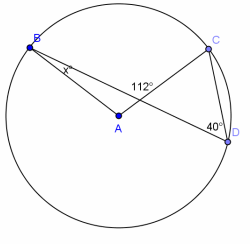
Answer:
x = 32
d.
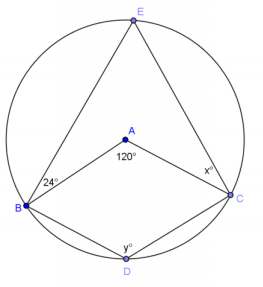
Answer:
x = 36, y = 120
e.
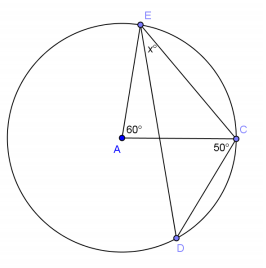
Answer:
x = 40
f.
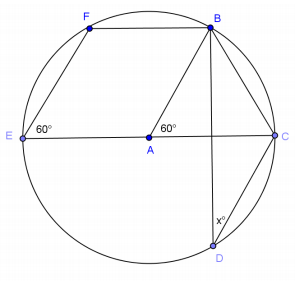
Answer:
x = 30
Eureka Math Geometry Module 5 Lesson 5 Problem Set Answer Key
For Problems 1–8, find the value of x. Diagrams are not drawn to scale.
Question 1.
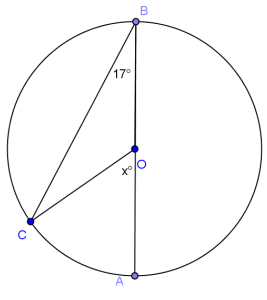
Answer:
x = 34
Question 2.
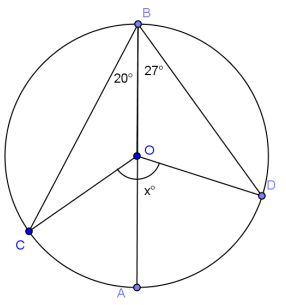
Answer:
x = 94
Question 3.
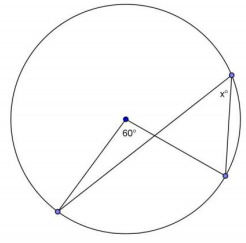
Answer:
x = 30
Question 4.
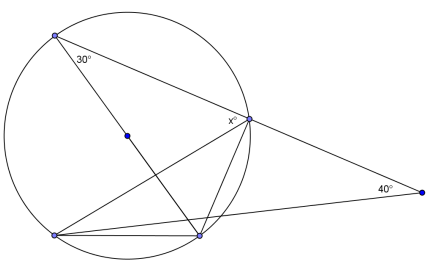
Answer:
x = 70
Question 5.
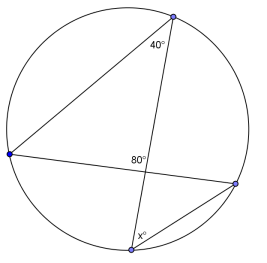
Answer:
x = 60
Question 6.
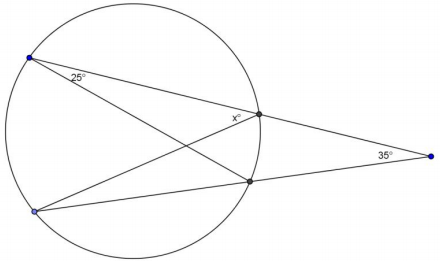
Answer:
x = 60
Question 7.
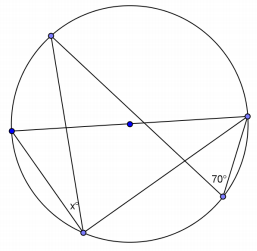
Answer:
x = 20
Question 8.
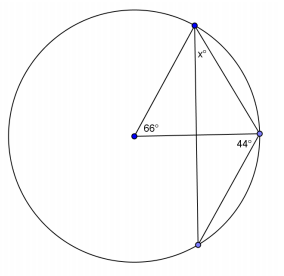
Answer:
x = 46
Question 9.
a. The two circles shown intersect at E and F. The center of the larger circle, D, lies on the circumference of the smaller circle. If a chord of the larger circle, (FG) ̅, cuts the smaller circle at H, find x and y.
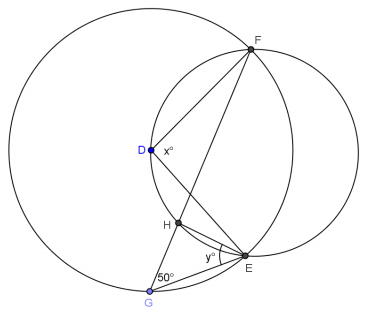
Answer:
x = 100; y = 50
b. How does this problem confirm the inscribed angle theorem?
Answer:
∠FDE is a central angle of the larger circle and is double ∠FGE, the inscribed angle of the larger circle. ∠FDE is inscribed in the smaller circle and equal in measure to ∠FHE, which is also inscribed in the smaller circle.
Question 10.
In the figure below, \(\overline{E D}\) and \(\overline{B C}\) intersect at point F.
Prove: m∠DAB + m∠EAC = 2(m∠BFD)
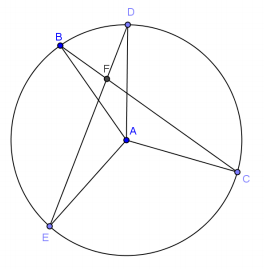
Proof:
Join \(\overline{B E}\).
m∠BED = \(\frac{1}{2}\)(m∠___________)
m∠EBC = \(\frac{1}{2}\)(m∠___________)
In △EBF,
m∠BEF + m∠EBF = m∠___________
\(\frac{1}{2}\)(m∠___________) + \(\frac{1}{2}\)(m∠___________) = m∠___________
∴ m∠DAB + m∠EAC = 2(m∠BFD)
Answer:
BAD; EAC; BFD; DAB, EAC, BFD
Eureka Math Geometry Module 5 Lesson 5 Exit Ticket Answer Key
Question 1.
The center of the circle below is O. If angle B has a measure of 15 degrees, find the values of x and y. Explain how you know.
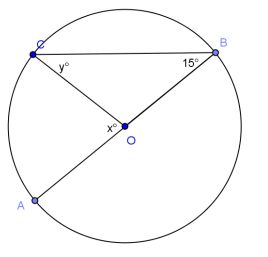
Answer:
y = 15. Triangle COB is isosceles, so base angles ∠OCB and ∠OBC are congruent. m∠OBC = 15˚ = m∠OCB.
x = 30. ∠COA is a central angle inscribed in the same arc as inscribed ∠CBA. So, m∠COA = 2(m∠CBA).