Engage NY Eureka Math Geometry Module 5 Lesson 4 Answer Key
Eureka Math Geometry Module 5 Lesson 4 Exploratory Challenge Answer Key
Exploratory Challenge 1
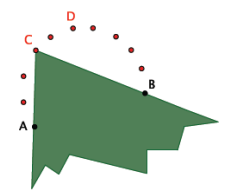
Your teacher will provide you with a straightedge, a sheet of colored paper in the shape of a trapezoid, and a sheet of plain white paper.
Draw two points no more than 3 inches apart in the middle of the plain white paper, and label them A and B.
Use the acute angle of your colored trapezoid to plot a point on the white sheet by placing the colored cutout so that the points A and B are on the edges of the acute angle and then plotting the position of the vertex of the angle. Label that vertex C.
Repeat several times. Name the points D, E, ….
Answer:
The students’ task is as appears below:
Exploratory Challenge 2
a. Draw several of the angles formed by connecting points A and B on your paper with any of the additional points you marked as the acute angle was pushed through the points (C, D, E, …). What do you notice about the measures of these angles?
Answer:
All angles have the same measure—the measure of the acute angle on the trapezoid.
b. Draw several of the angles formed by connecting points A and B on your paper with any of the additional points you marked as the obtuse angle was pushed through the points from above. What do you notice about the measures of these angles?
Answer:
All angles have the same measure—the measure of the obtuse angle on the trapezoid.
Exploratory Challenge 3
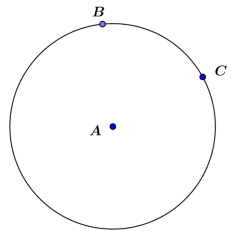
a. Draw a point on the circle, and label it D. Create angle ∠BDC.
b. ∠BDC is called an inscribed angle. Can you explain why?
Answer:
The vertex is on the circle, and the sides of the angle pass through points that are also on the circle.
c. Arc BC is called the intercepted arc. Can you explain why?
Answer:
It is the arc cut in the circle by the inscribed angle.
d. Carefully cut out the inscribed angle, and compare it to the angles of several of your neighbors.
e. What appears to be true about each of the angles you drew?
Answer:
All appear to have the same measure.
f. Draw another point on a second circle, and label it point E. Create ∠BEC, and cut it out. Compare ∠BDC and ∠BEC. What appears to be true about the two angles?
Answer:
All appear to have the same measure.
g. What conclusion may be drawn from this? Will all angles inscribed in the circle from these two points have the same measure?
Answer:
All angles inscribed in the circle from these two points will have the same measure.
h. Explain to your neighbor what you have just discovered.
Exploratory Challenge 4
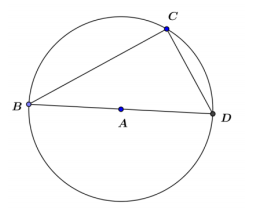
a. In the circle below, draw the angle formed by connecting points B and C to the center of the circle.
b. Is ∠BAC an inscribed angle? Explain.
Answer:
No. The vertex is not on the circle; the vertex is the center of the circle.
c. Is it appropriate to call this the central angle? Why or why not?
Answer:
The acute angle (∠BAC) is formed by connecting points B and C to the center point (A), so it would be appropriate to call this a central angle but not “the” central angle which implies there is only one central angle.
d. What is the intercepted arc?
Answer:
The intercepted arc is \(\widehat{B C}\).
e. Is the measure of ∠BAC the same as the measure of one of the inscribed angles in Exploratory Challenge 2?
Answer:
No, the measure of ∠BAC is greater.
f. Can you make a prediction about the relationship between the inscribed angle and the central angle?
Answer:
The inscribed angle is about half the central angle. The central angle is double the inscribed angle.
Eureka Math Geometry Module 5 Lesson 4 Exercise Answer Key
Opening Exercise
ARC:
Answer:
An arc is a portion of the circumference of a circle.
MINOR AND MAJOR ARC:
Answer:
Let C be a circle with center O, and let A and B be different points that lie on C but are not the endpoints of the same diameter. The minor arc is the set containing A, B, and all points of C that are in the interior of ∠AOB. The major arc is the set containing A, B, and all points of C that lie in the exterior of ∠AOB. Examples: Minor Arc \(\widehat{B E}\), \(\widehat{E D}\). Major Arc \(\widehat{E D B}\), \(\widehat{D C E}\). Answers will vary.
INSCRIBED ANGLE:
Answer:
An inscribed angle is an angle whose vertex is on a circle and each side of the angle intersects the circle in another point. Examples: ∠BDC, ∠ECD. Answers will vary.
CENTRAL ANGLE:
Answer:
A central angle of a circle is an angle whose vertex is the center of a circle. Examples: ∠CAB, ∠BAE. Answers will vary.
INTERCEPTED ARC OF AN ANGLE:
Answer:
An angle intercepts an arc if the endpoints of the arc lie on the angle, all other points of the arc are in the interior of the angle, and each side of the angle contains an endpoint of the arc. Examples: \(\widehat{E D}\), \(\widehat{C F}\). Answers will vary.
Eureka Math Geometry Module 5 Lesson 4 Problem Set Answer Key
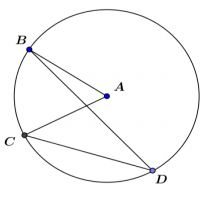
Question 1.
Using a protractor, measure both the inscribed angle and the central angle shown on the circle below.
m∠BCD = __________
Answer:
m∠BCD = 90°
m∠BAD = __________
Answer:
m∠BAD = 180°
Question 2.
Using a protractor, measure both the inscribed angle and the central angle shown on the circle below.
m∠BDC = __________
Answer:
m∠BDC = 30°
m∠BAC = __________
Answer:
m∠BAC = 60°
Question 3.
Using a protractor, measure both the inscribed angle and the central angle shown on the circle below.
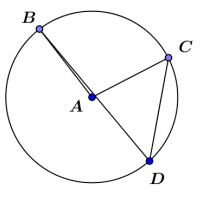
m∠BDC = __________
Answer:
m∠BDC = 50°
m∠BAC = __________
Answer:
m∠BAC = 100°
Question 4.
What relationship between the measure of the inscribed angle and the measure of the central angle that intercepts the same arc is illustrated by these examples?
Answer:
The measure of the inscribed angle appears to be half the measure of the central angle that intercepts the same arc.
Question 5.
Is your conjecture at least true for inscribed angles that measure 90°?
Answer:
Yes, according to Thales’ theorem, if A, B, and C are points on a circle where \(\overline{A C}\) is a diameter of the circle, then ∠ABC is a right angle. Since a diameter represents a 180° angle, our conjecture is always true for angles that measure 90°.
Question 6.
Prove that y = 2x in the diagram below.
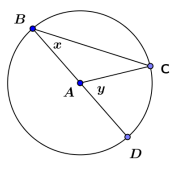
Answer:
△ABC is an isosceles triangle since all radii of a circle are congruent. Therefore, m∠B = m∠C = x. In addition, y = m∠B + m∠C since the measure of an exterior angle of a triangle is equal to the sum of the measures of the opposite interior angles. By substitution, y = x + x, or y = 2x.
Question 7.
Red (R) and blue (B) lighthouses are located on the coast of the ocean. Ships traveling are in safe waters as long as the angle from the ship (S) to the two lighthouses (∠RSB) is always less than or equal to some angle θ called the danger angle. What happens to θ as the ship gets closer to shore and moves away from shore? Why do you think a larger angle is dangerous?
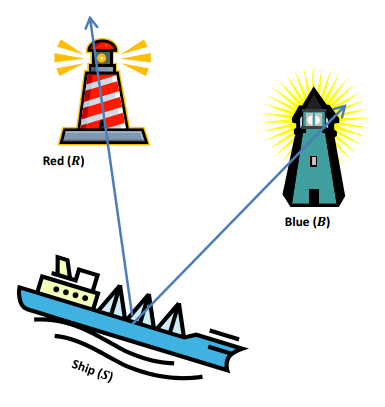
Answer:
The closer the boat is to the shore, the larger θ will be, and as the boat moves away from shore, θ gets smaller. A smaller θ means the ship is in deeper water, which is safer for ships.
Eureka Math Geometry Module 5 Lesson 4 Exit Ticket Answer Key
Joey marks two points on a piece of paper, as we did in the Exploratory Challenge, and labels them A and B. Using the trapezoid shown below, he pushes the acute angle through points A and B from below several times so that the sides of the angle touch points A and B, marking the location of the vertex each time. Joey claims that the shape he forms by doing this is the minor arc of a circle and that he can form the major arc by pushing the obtuse angle through points A and B from above. “The obtuse angle has the greater measure, so it will form the greater arc,” states Joey.
Ebony disagrees, saying that Joey has it backwards. “The acute angle will trace the major arc,” claims Ebony.
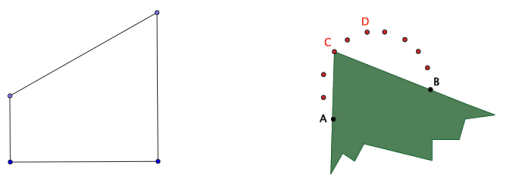
Question 1.
Who is correct, Joey or Ebony? Why?
Answer:
Ebony is correct. The acute angle vertex traces out the major arc of the circle.
Question 2.
How are the acute and obtuse angles of the trapezoid related?
Answer:
They are supplementary.
Question 3.
If Joey pushes one of the right angles through the two points, what type of figure is created? How does this relate to the major and minor arcs created above?
Answer:
A semicircle is created. Both arcs are the same measure (180°).