Engage NY Eureka Math Geometry Module 5 Lesson 3 Answer Key
Eureka Math Geometry Module 5 Lesson 3 Exercise Answer Key
Opening Exercise
Using only a compass and straightedge, find the location of the center of the circle below. Follow the steps provided.
- Draw chord \(\overline{A B}\).
- Construct a chord perpendicular to \(\overline{A B}\) at endpoint B.
- Mark the point of intersection of the perpendicular chord and the circle as point C.
- \(\overline{A C}\)is a diameter of the circle. Construct a second diameter in the same way.
- Where the two diameters meet is the center of the circle.

Answer:
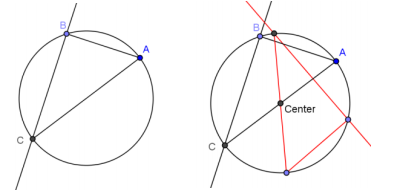
Explain why the steps of this construction work.
Answer:
The center is equidistant from all points on the circle. Since the diameter goes through the center, the intersection of any two diameters is a point on both diameters and must be the center.
Exercises
Exercise 1.
Construct a kite inscribed in the circle below, and explain the construction using symmetry.

Answer:
Construct △ABC as in the Opening Exercise, but this time reflect it across the diameter. It is a kite because, by reflection, there are two opposite pairs of congruent adjacent sides.
Exercise 2.
Given a circle and a rectangle, what must be true about the rectangle for it to be possible to inscribe a congruent copy of it in the circle?
Answer:
The diagonals of the rectangle must be the length of the diameter of the circle.
Exercise 3.
The figure below shows a rectangle inscribed in a circle.
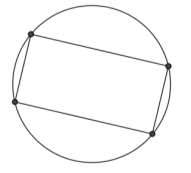
a. List the properties of a rectangle.
Answer:
Opposite sides are parallel and congruent, four right angles, and diagonals are congruent and bisect each other.
b. List all the symmetries this diagram possesses.
Answer:
Opposite sides are congruent, all four angles are congruent, diagonals are congruent, the figure may be reflected onto itself across the perpendicular bisector of the sides of the rectangle, and the figure may be rotated onto itself with either a 180° or a 360° rotation.
c. List the properties of a square.
Answer:
Opposite sides are parallel; all sides are congruent; four right angles; diagonals are congruent, bisect each other, and are perpendicular.
d. List all the symmetries of the diagram of a square inscribed in a circle.
Answer:
In addition to the symmetries listed in (b), all four sides are congruent, the figure may be reflected onto itself across the diagonals of the square, and the figure may be rotated onto itself with either a 90° or a 270° rotation either clockwise or counterclockwise.
Exercise 4.
A rectangle is inscribed into a circle. The rectangle is cut along one of its diagonals and reflected across that diagonal to form a kite. Draw the kite and its diagonals. Find all the angles in this new diagram, given that the acute angle formed by the diagonal of the rectangle in the original diagram was 40°.
Answer:
Draw diagrams such as the following:

Since a reflection is a rigid motion, m∠ADB = m∠BDE = 40°, m∠BAD = m∠BED = 90°, m∠ABD = m∠EBD = 50°. Then, m∠ABE = 100° and m∠ADE = 80°.
Exercise 5.
Challenge: Show that the three vertices of a right triangle are equidistant from the midpoint of the hypotenuse by showing that the perpendicular bisectors of the legs pass through the midpoint of the hypotenuse.
a. Draw the perpendicular bisectors of \(\overline{A B}\) and \(\overline{A C}\).
Answer:
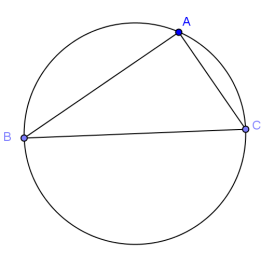
b. Label the point where they meet P. What is point P?
Answer:
The center of the circle
c. What can be said about the distance from P to each vertex of the triangle? What is the relationship between the circle and the triangle?
Answer:
Point P is equidistant from the three vertices of the triangle A, B, and C, so the circle is circumscribed about △ABC.
d. Repeat this process, this time sliding B to another place on the circle and call it B’. What do you notice?
Answer:
You get the same center.
e. Is there a relationship between m∠ABC and m∠AB’C? Explain.
Answer:
As long as B and B’ are on the same side of \(\overline{A C}\), then ∠ABC and ∠AB’C have the same measure because they are inscribed in the same arc. If B and B’ are not on the same side of \(\overline{A C}\), then m∠ABC ≠ m∠AB’ C because they are not inscribed in the same arc.
Eureka Math Geometry Module 5 Lesson 3 Problem Set Answer Key
Question 1.
Using only a piece of 8.5 × 11 inch copy paper and a pencil, find the location of the center of the circle below.
Answer:
Lay the paper across the circle so that its corner lies on the circle. The points where the two edges of the paper cross the circle are the endpoints of a diameter. Mark those points, and draw the diameter using the edge of the paper as a straightedge. Repeat to get a second diameter. The intersection of the two diameters is the center of the circle.
Question 2.
Is it possible to inscribe a parallelogram that is not a rectangle in a circle?
Answer:
No, although it is possible to construct an inscribed polygon with one pair of parallel sides (i.e., a trapezoid); a parallelogram requires that both pairs of opposite sides be parallel and both pairs of opposite angles be congruent. A parallelogram is symmetric by 180° rotation about its center and has NO other symmetry unless it is a rectangle. Two parallel lines and a circle create a figure that is symmetric by a reflection across the line through the center of the circle that is perpendicular to the two lines. If a trapezoid is formed with vertices where the parallel lines meet the circle, the trapezoid has reflectional symmetry. Therefore, it cannot be a parallelogram—unless it is a rectangle.
Question 3.
In the figure, BCDE is a rectangle inscribed in circle A. DE = 8; BE = 12. Find AE.
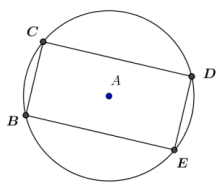
Answer:
2\(\sqrt{13}\)
Question 4.
Given the figure, BC = CD = 8 and AD = 13. Find the radius of the circle.
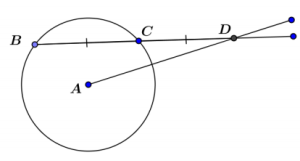
Answer:
Mark the midpoint of \(\overline{B C}\) as point E. BE = EC = 4, so ED = 12. △EAD is a right triangle, so by the Pythagorean theorem, EA = 5. Using the Pythagorean theorem again gives AC = \(\sqrt{41}\).
Question 5.
In the figure, \(\overline{D F}\) and \(\overline{B G}\) are parallel chords 14 cm apart. DF = 12 cm, AB = 10 cm, and \(\overline{E H}\) ⊥ \(\overline{B G}\). Find BG.
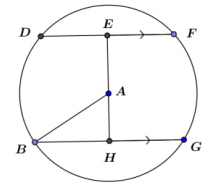
Answer:
Draw △DEA. m∠DEA = 90°, DE = 6 cm, DA = 10 cm. By the Pythagorean theorem, EA = 8 cm. In △ABH, m∠AHB = 90°, AB = 10 cm, AH = 6 cm, so BH = 8 cm. This means BG = 16 cm.
Question 6.
Use perpendicular bisectors of the sides of a triangle to construct a circle that circumscribes the triangle.
Answer:
(Students did a construction similar to this in Geometry, Module 1, Lesson 4.)
Draw any triangle.
Construct the perpendicular bisector of the sides.
The perpendicular bisectors meet at the circumcenter.
Using the center and the distance to one vertex as a radius, draw the circle.
Eureka Math Geometry Module 5 Lesson 3 Exit Ticket Answer Key
Question 1.
Rectangle ABCD is inscribed in circle P. Boris says that diagonal \(\overline{A C}\) could pass through the center, but it does not have to pass through the center. Is Boris correct? Explain your answer in words, or draw a picture to help you explain your thinking.
Answer:
Boris is not correct. Since each vertex of the rectangle is a right angle, the hypotenuse of the right triangle formed by each angle and the diagonal of the rectangle must be the diameter of the circle (by the work done in Lesson 1 of this module). The diameter of the circle passes through the center of the circle; therefore, the diagonal passes through the center.