Eureka Math Geometry Module 5 Lesson 2 Answer Key

Engage NY Eureka Math Geometry Module 5 Lesson 2 Answer Key

Eureka Math Geometry Module 5 Lesson 2 Exercise Answer Key

Opening Exercise
Construct the perpendicular bisector of \(\overline{A B}\) below (as you did in Module 1).

Draw another line that bisects \(\overline{A B}\) but is not perpendicular to it.
List one similarity and one difference between the two bisectors.
Answer:
Answers will vary. Both bisectors divide the segment into two shorter segments of equal length. All points on the perpendicular bisector are equidistant from points A and B. Points on the other bisector are not equidistant from points A and B. The perpendicular bisector meets \(\overline{A B}\) at right angles. The other bisector meets at angles that are not congruent.

Exercises
Exercise 1.
Prove the theorem: If a diameter of a circle bisects a chord, then it must be perpendicular to the chord.
Answer:
Draw a diagram similar to that shown below.

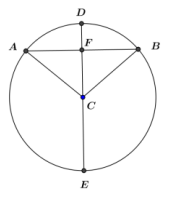
Given: Circle C with diameter \(\overline{D E}\), chord \(\overline{A B}\), and AF = BF
Prove: \(\overline{D E}\)⊥\(\overline{A B}\)
AF = BF        Given
FC = FC       Reflexive property
AC = BC        Radii of the same circle are equal in measure.
△AFC ≅ △BFC      SSS
m∠AFC = m∠BFC      Corresponding angles of congruent triangles are equal in measure.
∠AFC and ∠BFC are right angles Equal angles that form a linear pair each measure 90°.
\(\overline{D E}\) ⊥\(\overline{A B}\) Definition of perpendicular lines
OR
AF = BF    Given
AC = BC       Radii of the same circle are equal in measure.
m∠FAC = m∠FBC      Base angles of an isosceles triangle are equal in measure.
△AFC ≅ △BFC      SAS
m∠AFC = m∠BFC       Corresponding angles of congruent triangles are equal in measure.
∠AFC and ∠BFC are right angles Equal angles that form a linear pair each measure 90°.
\(\overline{D E}\) ⊥ \(\overline{A B}\) Definition of perpendicular lines

Exercise 2.
Prove the theorem: If a diameter of a circle is perpendicular to a chord, then it bisects the chord.
Answer:
Use a diagram similar to that in Exercise 1.
Given: Circle C with diameter \(\overline{D E}\), chord \(\overline{A B}\), and \(\overline{D E}\)⊥\(\overline{A B}\)
Prove: \(\overline{D E}\) bisects \(\overline{A B}\)
\(\overline{D E}\)⊥\(\overline{A B}\) Given
∠AFC and ∠BFC are right angles Definition of perpendicular lines
△AFC and △BFC are right triangles Definition of right triangle
∠AFC ≅∠BFC All right angles are congruent.
FC = FC Reflexive property
AC = BC Radii of the same circle are equal in measure.
△AFC ≅ △BFC HL
AF = BF Corresponding sides of congruent triangles are equal in length.
\(\overline{D E}\) bisects \(\overline{A B}\) Definition of segment bisector
OR
\(\overline{D E}\) ⊥\(\overline{A B}\)Given
∠AFC and ∠BFC are right angles Definition of perpendicular lines
∠AFC ≅∠BFC All right angles are congruent.
AC = BC Radii of the same circle are equal in measure.
m∠FAC = m∠FBC Base angles of an isosceles triangle are congruent.
m∠ACF = m∠BCF Two angles of triangle are equal in measure, so third angles are equal.
△AFC ≅ △BFC ASA
AF = BF Corresponding sides of congruent triangles are equal in length.
\(\overline{D E}\) bisects \(\overline{A B}\) Definition of segment bisector

Exercise 3.
The distance from the center of a circle to a chord is defined as the length of the perpendicular segment from the center to the chord. Note that since this perpendicular segment may be extended to create a diameter of the circle, the segment also bisects the chord, as proved in Exercise 2.
Prove the theorem: In a circle, if two chords are congruent, then the center is equidistant from the two chords.
Use the diagram below.

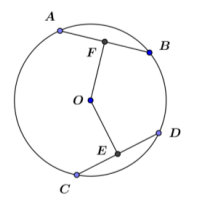
Answer:
Given: Circle O with chords \(\overline{A B}\) and \(\overline{C D}\); AB = CD; F is the midpoint of \(\overline{A B}\)and E is the midpoint of \(\overline{C D}\).
Prove: OF = OE
AB = CD Given
\(\overline{O F}\)and \(\overline{O E}\) are portions of diameters Definition of diameter
\(\overline{O F}\)⊥\(\overline{A B}\); \(\overline{O E}\)⊥\(\overline{C D}\) If a diameter of a circle bisects a chord, then the diameter must be perpendicular to the chord.
∠AFO and ∠DEO are right angles Definition of perpendicular lines
△AFO and △DEO are right triangles Definition of right triangle
E and F are midpoints of \(\overline{C D}\) and \(\overline{A B}\) Given
AF = DE AB = CD and F and E are midpoints of \(\overline{A B}\)and \(\overline{C D}\).
AO = DO All radii of a circle are equal in measure.
△AFO ≅ △DEO HL
OE = OF Corresponding sides of congruent triangles are equal in length.

Exercise 4.
Prove the theorem: In a circle, if the center is equidistant from two chords, then the two chords are congruent.
Use the diagram below.

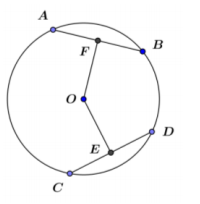
Answer:
Given: Circle O with chords \(\overline{A B}\)and \(\overline{C D}\); OF = OE; F is the midpoint of \(\overline{A B}\)and E is the midpoint of \(\overline{C D}\).
Prove: AB = CD
OF = OE Given
\(\overline{O F}\) and \(\overline{O E}\) are portions of diameters Definition of diameter
\(\overline{O F}\) ⊥\(\overline{A B}\), \(\overline{O E}\)⊥\(\overline{C D}\) If a diameter of a circle bisects a chord, then it must be perpendicular to the chord.
∠AFO and ∠DEO are right angles Definition of perpendicular lines
△AFO and △DEO are right triangles Definition of right triangle
AO = DO All radii of a circle are equal in measure.
△AFO ≅ △DEO HL
AF = DE Corresponding sides of congruent triangles are equal in length.
F is the midpoint of \(\overline{A B}\), and E is the
midpoint of \(\overline{C D}\). Given
AB = CD AF = DE and F and E are midpoints of \(\overline{A B}\) and \(\overline{C D}\).

Exercise 5.
A central angle defined by a chord is an angle whose vertex is the center of the circle and whose rays intersect the circle. The points at which the angle’s rays intersect the circle form the endpoints of the chord defined by the central angle.
Prove the theorem: In a circle, congruent chords define central angles equal in measure.
Use the diagram below.

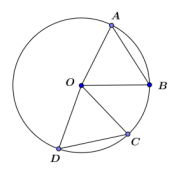
Answer:
We are given that the two chords (\(\overline{A B}\) and \(\overline{C D}\)) are congruent. Since all radii of a circle are congruent, \(\overline{A O}\) ≅ \(\overline{B O}\) ≅ \(\overline{C O}\) ≅ \(\overline{D O}\). Therefore, △ABO ≅ △DCO by SSS. ∠AOB ≅ ∠DOC since corresponding angles of congruent triangles are equal in measure.

Exercise 6.
Prove the theorem: In a circle, if two chords define central angles equal in measure, then they are congruent.
Answer:
Using the diagram from Exercise 5, we now are given that m∠AOB = m∠COD. Since all radii of a circle are congruent, \(\overline{A O}\) ≅ \(\overline{B O}\) ≅ \(\overline{C O}\) ≅ \(\overline{D O}\). Therefore, △ABO≅ △DCO by SAS. \(\overline{A B}\) ≅ \(\overline{D C}\) because corresponding sides of congruent triangles are congruent.

Eureka Math Geometry Module 5 Lesson 2 Problem Set Answer Key

Question 1.
In this drawing, AB = 30, OM = 20, and ON = 18. What is CN?

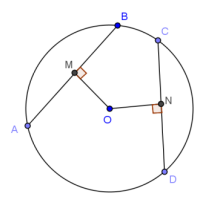
Answer:
\(\sqrt{301}\) ≈ 17.35

Question 2.
In the figure to the right, \(\overline{A C}\)⊥\(\overline{B G}\), \(\overline{D F}\)⊥\(\overline{E G}\), and EF = 12. Find AC.

Answer:
24

Question 3.
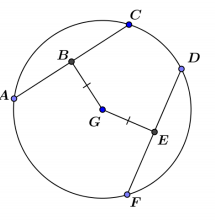
In the figure, AC = 24, and DG = 13. Find EG. Explain your work.

Answer:
5, △ABG is a right triangle with hypotenuse = radius = 13 and AB = 12, so BG = 5 by Pythagorean theorem. BG = GE = 5.

Question 4.
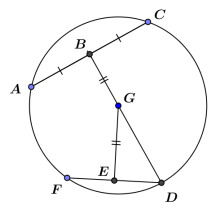
In the figure, AB = 10, and AC = 16. Find DE.

Answer:
4

Question 5.
In the figure, CF = 8, and the two concentric circles have radii of 10 and 17. Find DE.

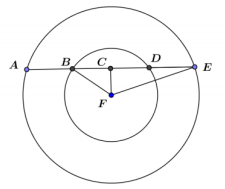
Answer:
9

Question 6.
In the figure, the two circles have equal radii and intersect at points B and D. A and C are centers of the circles. AC = 8, and the radius of each circle is 5. \(\overline{B D}\) ⊥ \(\overline{A C}\). Find BD. Explain your work.

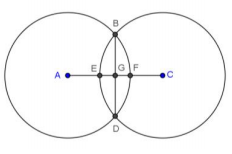
Answer:
6
BA = BC = 5 (radii)
AG = GC = 4
BG = 3 (Pythagorean theorem)
BD = 6

Question 7.
In the figure, the two concentric circles have radii of 6 and 14. Chord (BF) ̅ of the larger circle intersects the smaller circle at C and E. CE = 8. \(\overline{A D}\)⊥\(\overline{B F}\).

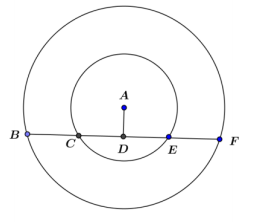
a. Find AD.
2\(\sqrt{5}\)

b. Find BF.
Answer:
8\(\sqrt{11}\)

Question 8.
In the figure, A is the center of the circle, and CB = CD. Prove that \(\overline{A C}\) bisects ∠BCD.

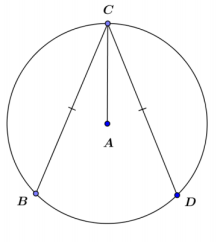
Answer:
Let \(\overline{A E}\) and \(\overline{A F}\) be perpendiculars from A to \(\overline{C B}\) and \(\overline{C D}\), respectively.
CB = CD Given
AE = AF If two chords are congruent, then the center is equidistant from the two chords.
AC = AC Reflexive property
m∠CEA = m∠CFA = 90° Definition of perpendicular
△CEA ≅ △CFA HL
m∠ECA = m∠FCA Corresponding angles of congruent triangles are equal in measure.
\(\overline{A C}\) bisects ∠BCD Definition of angle bisector

Question 9.
In class, we proved: Congruent chords define central angles equal in measure.
a. Give another proof of this theorem based on the properties of rotations. Use the figure from Exercise 5.
Answer:

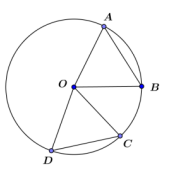
We are given that the two chords (\(\overline{A B}\) and \(\overline{C D}\)) are congruent. Therefore, a rigid motion exists that carries \(\overline{A B}\) to \(\overline{C D}\). The same rotation that carries \(\overline{A B}\) to \(\overline{C D}\) also carries \(\overline{A O}\) to \(\overline{C O}\) and \(\overline{B O}\) to \(\overline{D O}\). The angle of rotation is the measure of ∠AOC, and the rotation is clockwise.

b. Give a rotation proof of the converse: If two chords define central angles of the same measure, then they must be congruent.
Answer:
Using the same diagram, we are given that ∠AOB ≅∠COD. Therefore, a rigid motion (a rotation) carries ∠AOB to ∠COD. This same rotation carries \(\overline{A O}\) to \(\overline{C O}\) and \(\overline{B O}\) to \(\overline{D O}\). The angle of rotation is the measure of ∠AOC, and the rotation is clockwise.

Eureka Math Geometry Module 5 Lesson 2 Exit Ticket Answer Key

Question 1.
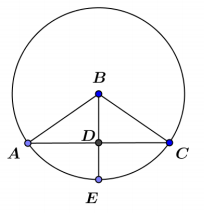
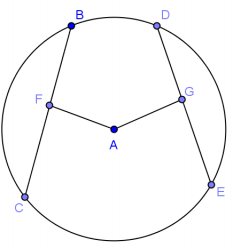
Given circle A shown, AF = AG and BC = 22. Find DE.

Answer:
22

Question 2.
In the figure, circle P has a radius of 10. \(\overline{A B}\)⊥\(\overline{D E}\).

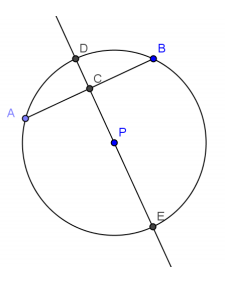
a. If AB = 8, what is the length of \(\overline{A C\)?
Answer:
4

b. If DC = 2, what is the length of \(\overline{A B}\)?
Answer:
12