Engage NY Eureka Math Geometry Module 5 Lesson 18 Answer Key
Eureka Math Geometry Module 5 Lesson 18 Example Answer Key
Example 1.
The following is the equation of a circle with radius 5 and center (1, 2). Do you see why?
x2 – 2x + 1 + y2 – 4y + 4 = 25
Answer:
→ We know that the equation x2 – 2x + 1 + y2 – 4y + 4 = 25 is a circle with radius 5 and center (1, 2) because when we multiply out the equation (x – 1)2 + (y – 2)2 = 52, we get
x2 – 2x + 1 + y2 – 4y + 4 = 25.
→ Provide students time to verify that these equations are equal.
→ Recall the equation for a circle with center (a, b) and radius r from the previous lesson.
(x – a)2 + (y – b)2 = r2
→ Multiply out each of the binomials to write an equivalent equation.
x2 – 2ax + a2 + y2 – 2by + b2 = r2
→ Sometimes equations of circles are presented in this simplified form. To easily identify the center and the radius of the graph of the circle, we sometimes need to factor and/or complete the square in order to rewrite the equation in its standard form (x – a)2 + (y – b)2 = r2.
Example 2.
What is the center and radius of the following circle?
x2 + 4x + y2 – 12y = 41
Answer:
We can complete the square, twice, in order to rewrite the equation in the necessary form.
First, x2 + 4x:
x2 + 4x + 4 = (x + 2)2
Second, y2 – 12y:
y2 – 12y + 36 = (y – 6)2
Then,
x2 + 4x + y2 – 12y = 41
(x2 + 4x + 4) + (y2 – 12y + 36) = 41 + 4 + 36
(x + 2)2 + (y – 6)2 = 81″.”
Therefore, the center is at ( – 2, 6), and the radius is 9.
Example 3.
Could x2 + y2 + Ax + By + C = 0 represent a circle?
Answer:
Let students think about this. Answers will vary.
Eureka Math Geometry Module 5 Lesson 18 Exercise Answer Key
Opening Exercise
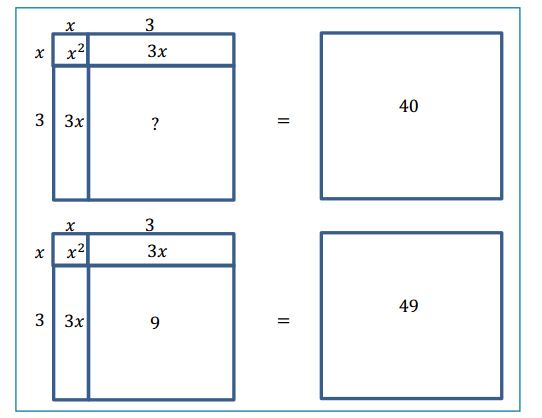
a. Express this as a trinomial: (x – 5)2.
Answer:
(x – 5)2 = x2 – 10x + 25
b. Express this as a trinomial: (x + 4)2.
Answer:
(x + 4)2 = x2 + 8x + 16
c. Factor the trinomial: x2 + 12x + 36.
Answer:
x2 + 12x + 36 = (x + 6)2
d. Complete the square to solve the following equation: x2 + 6x = 40.
Answer:
x2 + 6x = 40
x2 + 6x + 9 = 40 + 9
(x + 3)2 = 49
x + 3 = 7
x = 4
Exercise 1.
Rewrite the following equations in the form (x – a)2 + (y – b)2 = r2.
a. x2 + 4x + 4 + y2 – 6x + 9 = 36
Answer:
(x + 2)2 + (y – 3)2 = 36
b. x2 – 10x + 25 + y2 + 14y + 49 = 4
Answer:
(x – 5)2 + (y + 7)2 = 4
Exercises 2–4
Exercise 2.
Identify the center and radius for each of the following circles.
a. x2 – 20x + y2 + 6y = 35
Answer:
(x – 10)2 + (y + 3)2 = 144
The center is (10, – 3), and the radius is 12.
b. x2 – 3x + y2 – 5y = \(\frac{19}{2}\)
Answer:
(x – \(\frac{3}{2}\))2 + (y – \(\frac{5}{2}\))2 = 18
The center is (\(\frac{3}{2}\), \(\frac{5}{2}\)), and the radius is \(\sqrt{18}\) = 3\(\sqrt{2}\).
Exercise 3.
Could the circle with equation x2 – 6x + y2 – 7 = 0 have a radius of 4? Why or why not?
Answer:
(x – 3)2 + y2 = 16
Yes, the radius is 4.
Exercise 4.
Stella says the equation x2 – 8x + y2 + 2y = 5 has a center of (4, – 1) and a radius of 5. Is she correct? Why or why not?
Answer:
(x – 4)2 + (y + 1)2 = 22
The center is (4, – 1), but the radius is \(\sqrt{22}\). She did not add the values to the right that she added to the left when completing the square.
Exercise 5.
a. Identify the graphs of the following equations as a circle, a point, or an empty set.
Answer:
x2 + y2 + 4x = 0
x2 + 4x + 4 + y2 = 4
(x + 2)2 + y2 = 4
The right side of the equation is positive, so the graph of the equation is a circle.
b. x2 + y2 + 6x – 4y + 15 = 0
Answer:
(x2 + 6x + 9) + (y2 – 4y + 4) + 15 = 13
(x + 3)2 + (y – 2)2 = – 2
The right side of the equation is negative, so the graph of this equation cannot be a circle; it is an empty set.
c. 2x2 + 2y2 – 5x + y + \(\frac{13}{4}\) = 0
Answer:
\(\frac{1}{2}\) (2x2 + 2y2 – 5x + y + \(\frac{13}{4}\)) = 0
x2 – \(\frac{5}{2}\) x + y2 + \(\frac{1}{2}\) y + \(\frac{13}{8}\) = 0
x2 – \(\frac{5}{2}\) x + (\(\frac{5}{4}\))2 + y2 + \(\frac{1}{2}\) y + (\(\frac{1}{4}\))2 + \(\frac{13}{8}\) = (\(\frac{5}{4}\))2 + (\(\frac{1}{4}\))2
(x – \(\frac{5}{4}\))2 + (y + \(\frac{1}{4}\))2 = – \(\frac{13}{8}\) + (\(\frac{5}{4}\))2 + (\(\frac{1}{4}\))2
(x – \(\frac{5}{4}\))2 + (y + \(\frac{1}{4}\))2 = – \(\frac{13}{8}\) + \(\frac{13}{8}\)
(x – \(\frac{5}{4}\))2 + (y + \(\frac{1}{4}\))2 = 0
The right side of the equation is equal to zero, so the graph of the equation is a point.
Eureka Math Geometry Module 5 Lesson 18 Problem Set Answer Key
Question 1.
Identify the centers and radii of the following circles.
a. (x + 25)2 + y2 = 1
Answer:
The center is ( – 25, 0), and the radius is 1.
b. x2 + 2x + y2 – 8y = 8
Answer:
(x + 1)2 + (y – 4)2 = 25
The center is ( – 1, 4), and the radius is 5.
c. x2 – 20x + y2 – 10y + 25 = 0
Answer:
(x – 10)2 + (y – 5)2 = 100
The center is (10, 5), and the radius is 10.
d. x2 + y2 = 19
Answer:
The center is (0, 0), and the radius is \(\sqrt{19}\).
e. x2 + x + y2 + y = – \(\frac{1}{4}\)
(x + \(\frac{1}{2}\))2 + (y + \(\frac{1}{2}\))2 = \(\frac{1}{4}\)
The center is ( – \(\frac{1}{2}\), – \(\frac{1}{2}\)), and the radius is \(\frac{1}{2}\).
Question 2.
Sketch graphs of the following equations.
a. x2 + y2 + 10x – 4y + 33 = 0
Answer:
(x + 5)2 + (y – 2)2 = – 4
The right side of the equation is negative, so its graph cannot be a circle. It is an empty set, and since there are no solutions, there is nothing to graph.
b. x2 + y2 + 14x – 16y + 104 = 0
Answer:
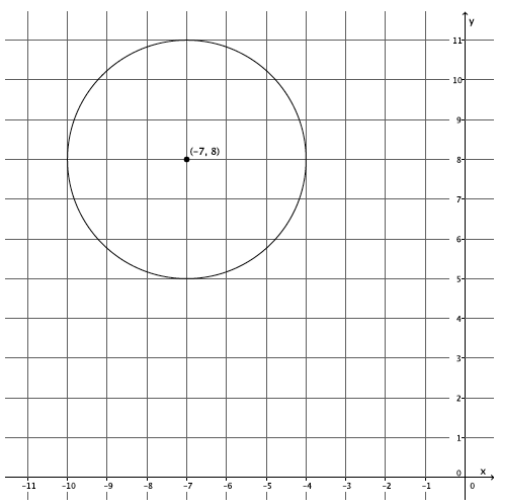
(x + 7)2 + (y – 8)2 = 9
The graph of the equation is a circle with center ( – 7, 8) and radius 3.
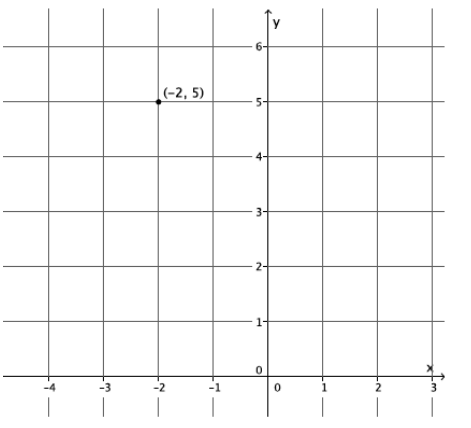
c. x2 + y2 + 4x – 10y + 29 = 0
Answer:
(x + 2)2 + (y – 5)2 = 0
The graph of this equation is a point at ( – 2, 5).
Question 3.
Chante claims that two circles given by (x + 2)2 + (y – 4)2 = 49 and x2 + y2 – 6x + 16y + 37 = 0 are externally tangent. She is right. Show that she is.
Answer:
(x + 2)2 + (y – 4)2 = 49
This graph of this equation is a circle with center ( – 2, 4) and radius 7.
(x – 3)2 + (y + 8)2 = 36
This graph of this equation is a circle with center (3, – 8) and radius 6.
By the distance formula, the distance between the two centers is 13, which is precisely the sum of the radii of the two circles. Therefore, these circles will touch only at one point. Put differently, they are externally tangent.
Question 4.
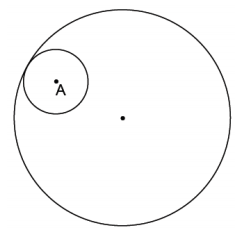
Draw a circle. Randomly select a point in the interior of the circle; label the point A. Construct the greatest radius circle with center A that lies within the circular region defined by the original circle. Hint: Draw a line through the center, the circle, and point A.
Answer:
Constructions will vary. Ensure that students have drawn two circles such that the circle with center A is in the interior and tangent to the original circle.
Eureka Math Geometry Module 5 Lesson 18 Exit Ticket Answer Key
Question 1.
The graph of the equation below is a circle. Identify the center and radius of the circle.
x2 + 10x + y2 – 8y – 8 = 0
Answer:
(x + 5)2 + (y – 4)2 = 49
The center is ( – 5, 4), and the radius is 7.
Question 2.
Describe the graph of each equation. Explain how you know what the graph will look like.
a. x2 + 2x + y2 = – 1
Answer:
(x + 1)2 + y2 = 0
The graph of this equation is a point. I can place a center at ( – 1, 0), but the radius is equal to zero. Therefore, the graph is just a single point.
b. x2 + y2 = – 3
Answer:
The right side of the equation is negative, so its graph cannot be a circle; it is an empty set.
c. x2 + y2 + 6x + 6y = 7
Answer:
(x + 3)2 + (y + 3)2 = 25
The graph of this equation is a circle with center ( – 3, – 3) and radius 5. Since the equation can be put in the form (x – a)2 + (y – b)2 = r2, I know the graph of it is a circle.