Engage NY Eureka Math Geometry Module 5 Lesson 16 Answer Key
Eureka Math Geometry Module 5 Lesson 16 Exploratory Challenge Answer Key
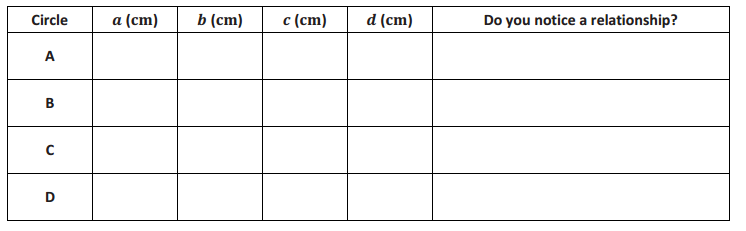
Exploratory Challenge 1
Measure the lengths of the chords in centimeters, and record them in the table.
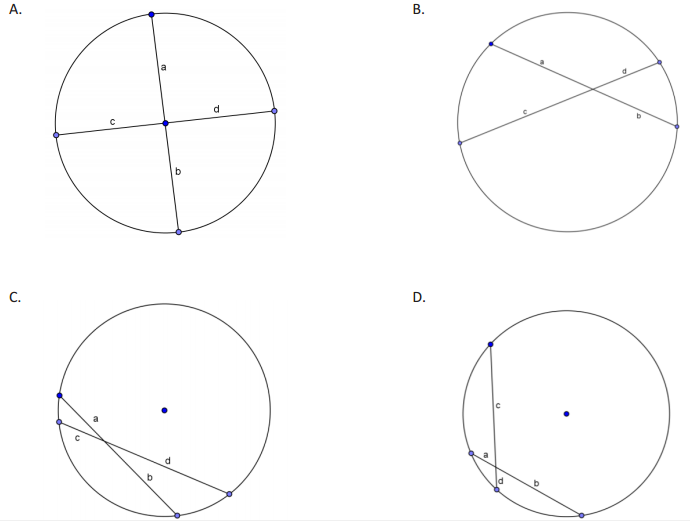
Answer:
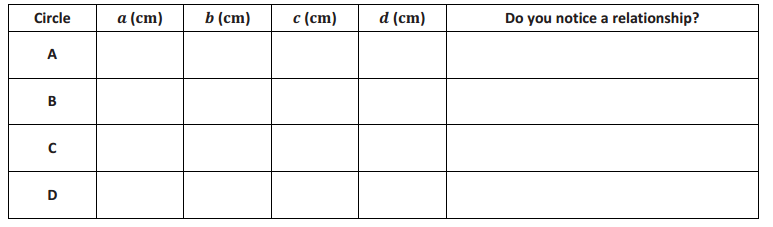
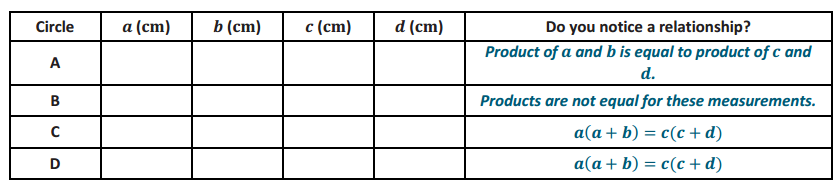
Exploratory Challenge 2
Measure the lengths of the chords in centimeters, and record them in the table.
Answer:
Eureka Math Geometry Module 5 Lesson 16 Exercise Answer Key
Opening Exercise
Identify the type of angle and the angle/arc relationship, and then find the measure of x.
a.
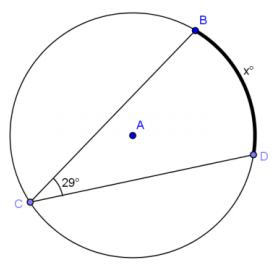
Answer:
x = 58; the inscribed angle is equal to half intercepted arc.
b.
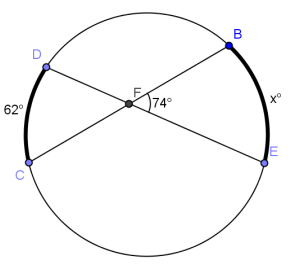
Answer:
x = 86; angle formed by secants intersecting inside the circle is half the sum of arcs intercepted by angle and its vertical angle.
c.
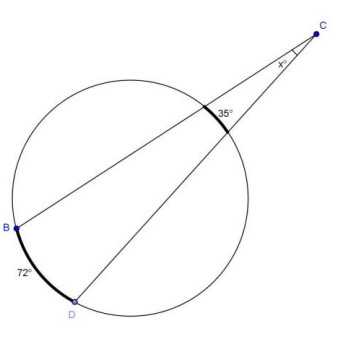
Answer:
x = 18.5; angle formed by secants intersecting outside of the circle has a measure of half the difference of larger and smaller intercepted arcs.
d.
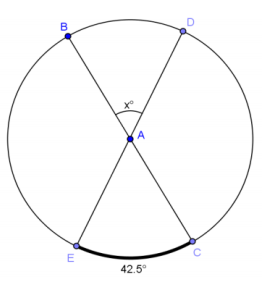
Answer:
x = 42.5; central angle has measure of intercepted arc.
Closing
The Inscribed Angle Theorem and Its Family
Answer:
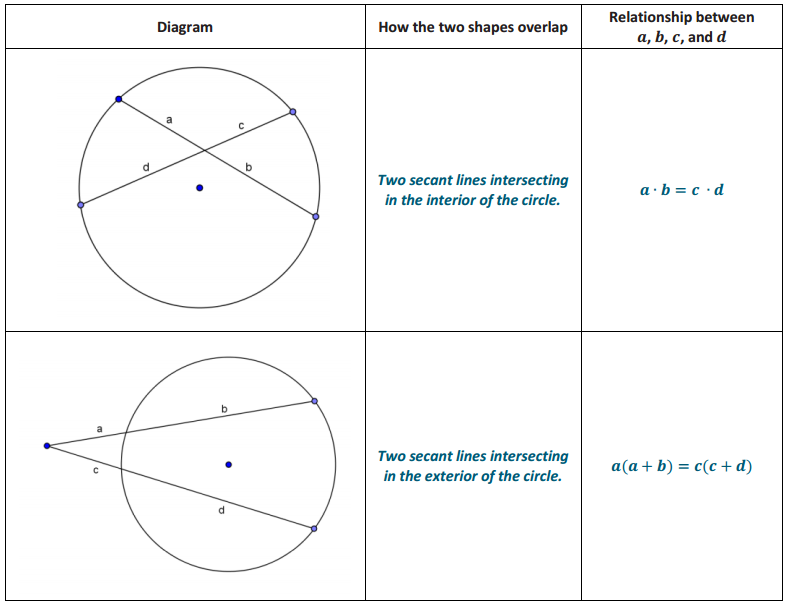
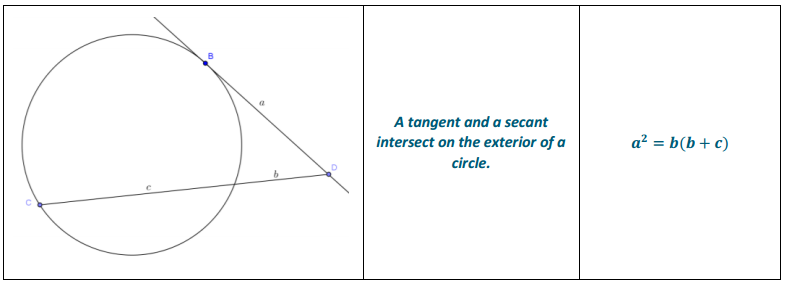
Eureka Math Geometry Module 5 Lesson 16 Problem Set Answer Key
Question 1.
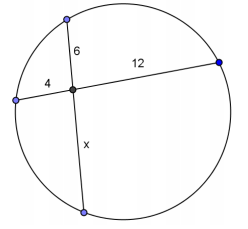
Answer:
x = 8
Question 2.
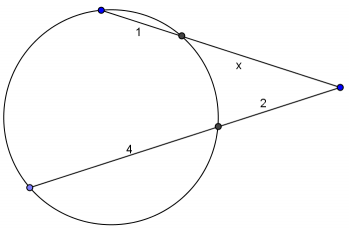
Answer:
x(x + 1) = 2(2 + 4)
x2 + x – 12 = 0
(x + 4)(x – 3) = 0
x = 3
Question 3.
DF < FB, DF ≠ 1, DF < FE, and all values are integers; prove DF = 3.
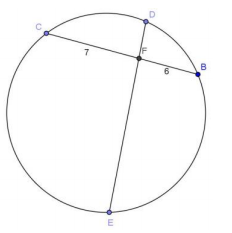
Answer:
7 ⋅ 6 = 42, so DF ⋅ FE must equal 42. If DF < FE, DF could equal 1, 3, or 6. DF ≠ 1 and DF < FB, so DF must equal 3.
Question 4.
CE = 6, CB = 9, and CD = 18. Show CF = 3.
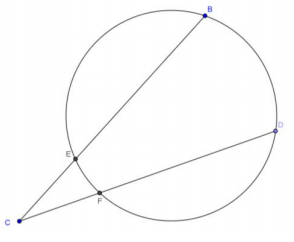
Answer:
6 ⋅ 9 = 54 and 18 ⋅ CF = 54. This means CF = 3.
Question 5.
Find x.
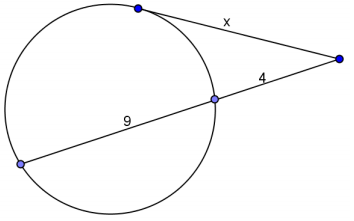
Answer:
x = 2\(\sqrt{13}\)
Question 6.
Find x.
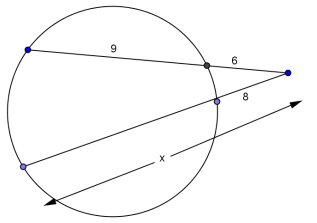
Answer:
x = 11.25
Question 7.
Find x.
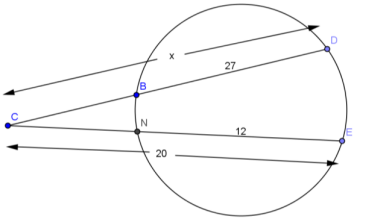
Answer:
(x – 27)x = 8(20)
x = 32
Question 8.
Find x.
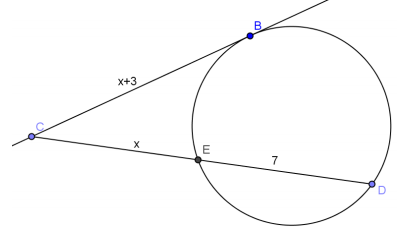
Answer:
x(x + 7) = (x + 3)2
x = 9
Question 9.
In the circle shown, DE = 11, BC = 10, and DF = 8. Find FE, BF, FC.
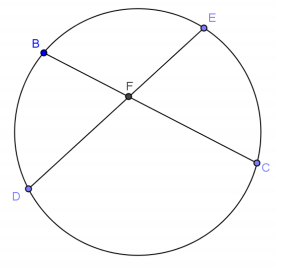
Answer:
x(10 – x) = (3)(8)
FE = 3, BF = 4, FC = 6
Question 10.
In the circle shown, \(m\widehat{D B G}\) = 150°, \(m\widehat{D B}\) = 30°, m∠CEF = 60°, DF = 8, DB = 4, and GF = 12.
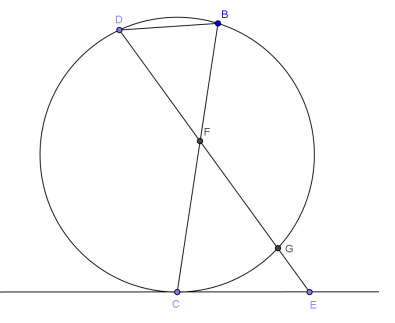
a. Find m∠GDB.
Answer:
60°
b. Prove △DBF ~ △ECF
Answer:
m∠DBF = m∠CEF Inscribed angle ∠DBF is half the measure of intercepted arc, \(\widehat{D C}\) and ∠CEF formed by a tangent line and a secant line is also half the measure of the same intercepted arc \(\widehat{D C}\).
m∠DFB = m∠EFC Vertical angles are equal in measure.
△DBF ~ △ECF AA
c. Set up a proportion using \(\overline{C E}\) and \(\overline{G E}\).
Answer:
\(\frac{8}{GE + 12}\) = \(\frac{4}{CE}\) , or 2CE = GE + 12
d. Set up an equation with CE and GE using a theorem for segment lengths from this section.
Answer:
CE2 = GE(GE + 20)
Eureka Math Geometry Module 5 Lesson 16 Exit Ticket Answer Key
Question 1.
In the circle below, \(m \widehat{G F}\) = 30°, \(m \widehat{D E}\) = 120°, CG = 6, GH = 2, FH = 3, CF = 4, HE = 9, and FE = 12.
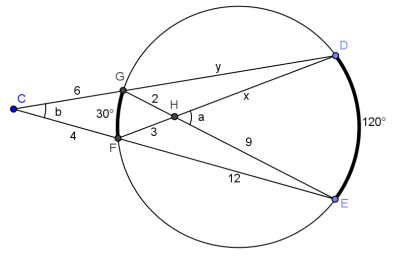
a. Find a (m∠DHE).
Answer:
a = 75°
b. Find b (m∠DCE), and explain your answer.
Answer:
b = 45°; b is an angle with its vertex outside of the circle, so it has a measure half the difference between its larger and smaller intercepted arcs.
c. Find x (HD), and explain your answer.
Answer:
x = 6; x is part of a secant line intersecting another secant line inside the circle, so 2∙9 = 3∙x.
d. Find y (\(\overline{D G}\)).
Answer:
y = \(\frac{14}{3}\) = 4 \(\frac{2}{3}\)