Engage NY Eureka Math Geometry Module 5 Lesson 15 Answer Key
Eureka Math Geometry Module 5 Lesson 15 Exploratory Challenge Answer Key
Exploratory Challenge
Shown below are two circles with two secant chords intersecting outside the circle.
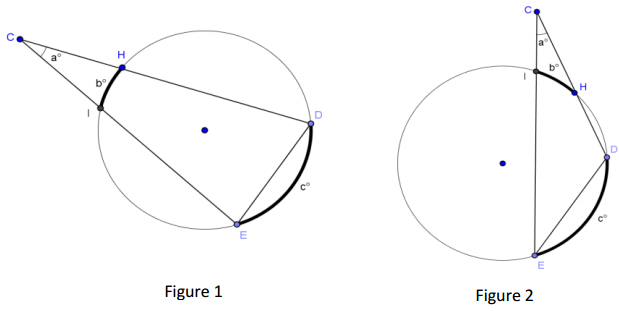
Measure a, b, and c. Make a conjecture about the relationship between them.

Answer:

Conjecture about the relationship between a, b, and c:
Answer:
The value of a is half the difference of the value of (c – b).
Test your conjecture with another diagram.
Eureka Math Geometry Module 5 Lesson 15 Exercise Answer Key
Opening Exercise
Question 1.
Shown below are circles with two intersecting secant chords.
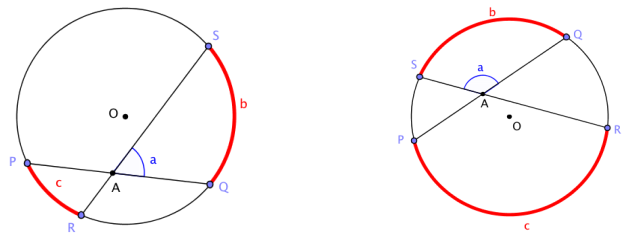
Measure a, b, and c in the two diagrams. Make a conjecture about the relationship between them.

Answer:

CONJECTURE about the relationship between a, b, and c:
Answer:
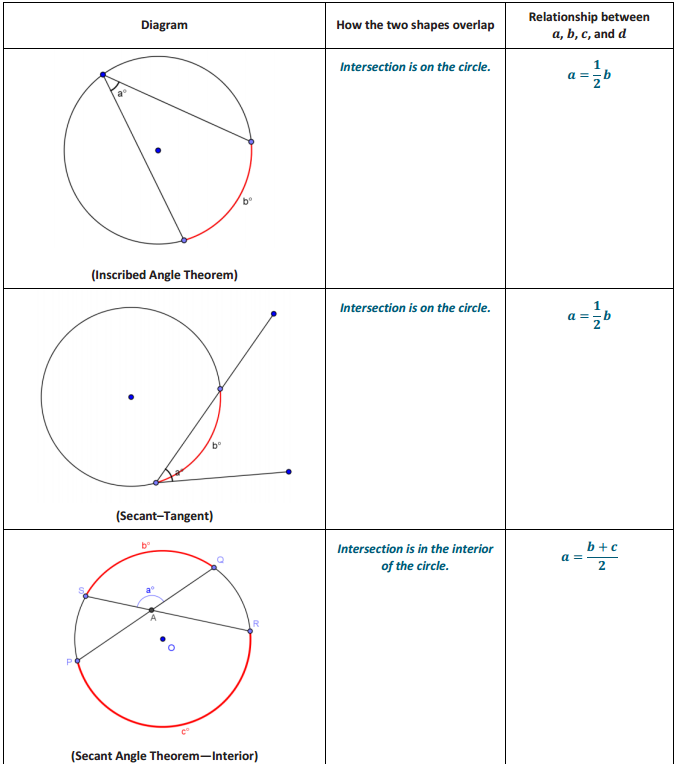
a = \(\frac{b + c}{2}\). The measure a is the average of b and c.
Question 2.
We will prove the following.
SECANT ANGLE THEOREM—INTERIOR CASE: The measure of an angle whose vertex lies in the interior of a circle is equal to half the sum of the angle measures of the arcs intercepted by it and its vertical angle.
We can interpret this statement in terms of the diagram below. Let b and c be the angle measures of the arcs intercepted by ∠SAQ and ∠PAR. Then measure a is the average of b and c; that is, a = latex]\frac{b + c}{2}[/latex].
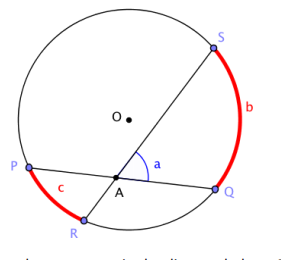
a. Find as many pairs of congruent angles as you can in the diagram below. Express the measures of the angles in terms of b and c whenever possible.
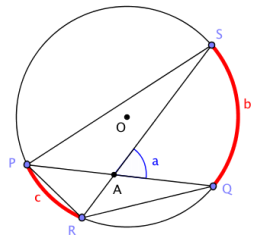
Answer:
m∠PQR = m∠PSR = \(\frac{1}{2}\) c
m∠QPS = m∠QRS = \(\frac{1}{2}\) b
b. Which triangles in the diagram are similar? Explain how you know.
Answer:
△PSA∼ △RQA. All angles in each pair have the same measure.
c. See if you can use one of the triangles to prove the secant angle theorem, interior case. (Hint: Use the exterior angle theorem.)
Answer:
By the exterior angle theorem, a = m∠PQR + m∠QRS. We can conclude a = \(\frac{1}{2}\)(b + c).
Exercises
Find x, y, and/or z.
Exercise 1.
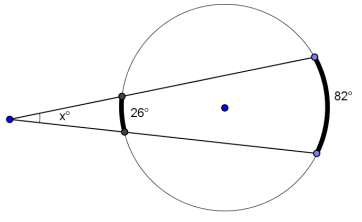
Answer:
x = 28
Exercise 2.
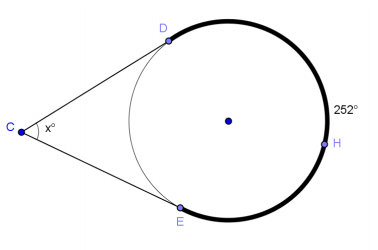
Answer:
x = 72
Exercise 3.
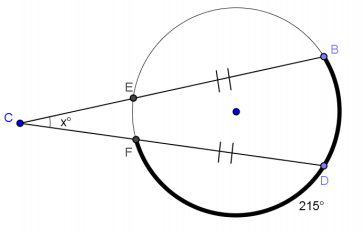
Answer:
x = 35
Exercise 4.
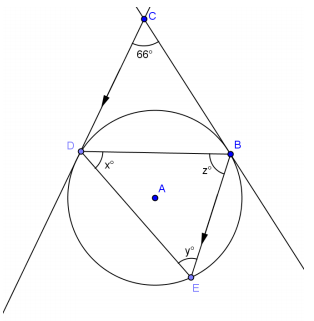
Answer:
x = 66, y = 57, z = 57
Closing Exercise
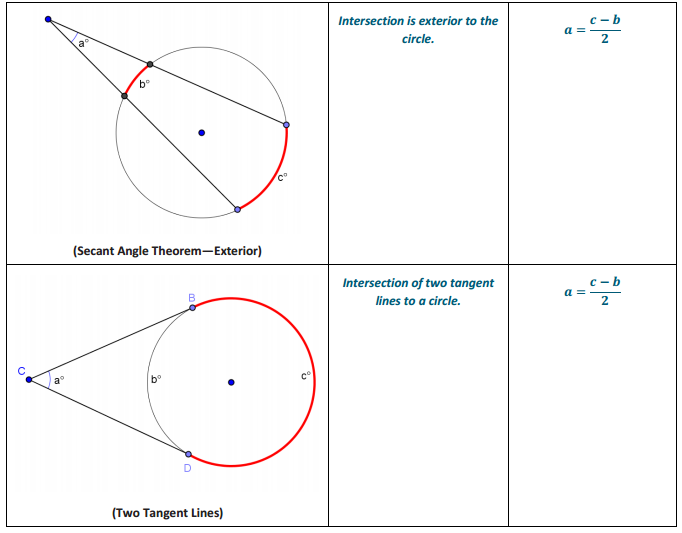
We have just developed proofs for an entire family of theorems. Each theorem in this family deals with two shapes and how they overlap. The two shapes are two intersecting lines and a circle.
In this exercise, you will summarize the different cases.
The Inscribed Angle Theorem and its Family of Theorems
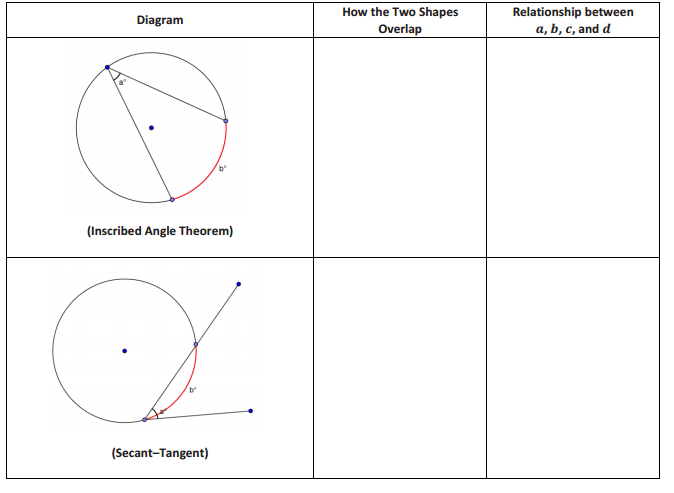
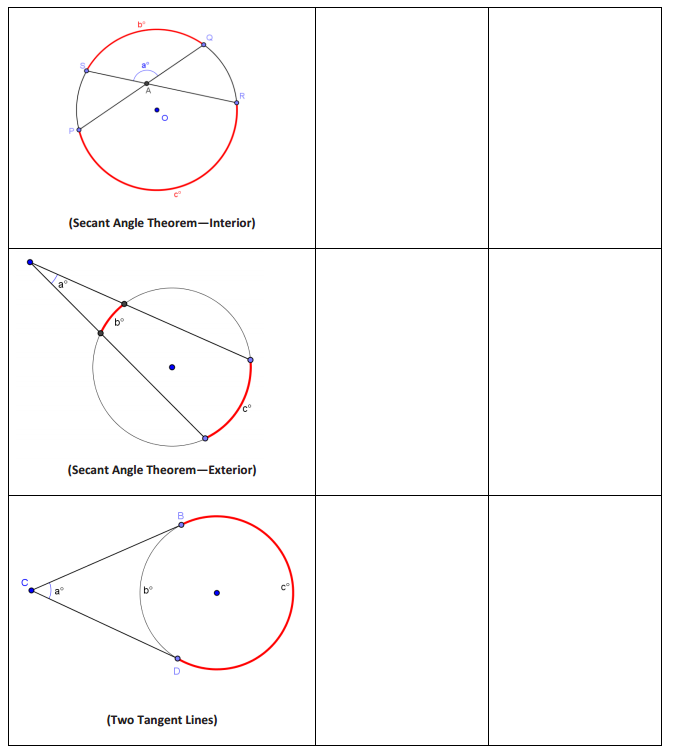
Answer:
Eureka Math Geometry Module 5 Lesson 15 Problem Set Answer Key
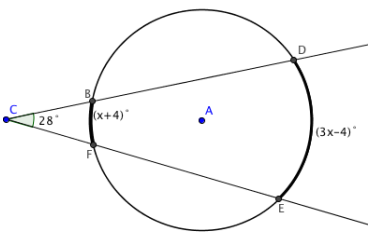
Question 1.
Find x.
Answer:
x = 32
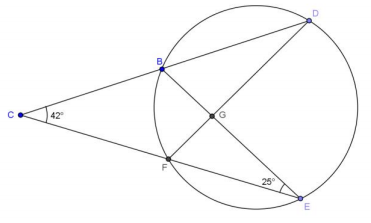
Question 2.
Find m∠DFE and m∠DGB.
Answer:
m∠DFE = 67°, m∠DGB = 88°
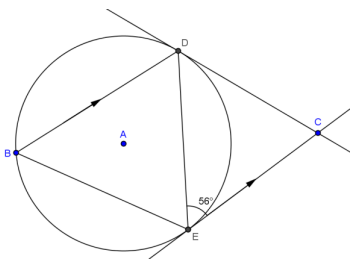
Question 3.
Find m∠ECD, m∠DBE, and m∠DEB.
Answer:
m∠ECD = 68°, m∠DBE = 56°, m∠DEB = 68°
Question 4.
Find m∠FGE and m∠FHE.
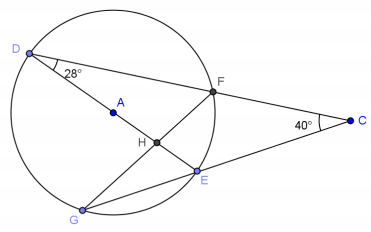
Answer:
m∠FGE = 28°, m∠FHE = 96°
Question 5.
Find x and y.
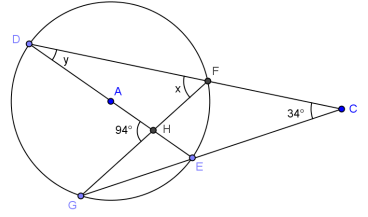
Answer:
x = 64°, y = 30°
Question 6.
The radius of circle A is 4. \(\overline{D C}\) and \(\overline{C E}\) are tangent to the circle with DC = 12. Find \(m \widehat{D E}\) and the area of quadrilateral DAEC rounded to the nearest hundredth.
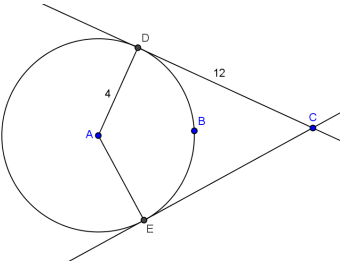
Answer:
m∠C = 2(tan – 1\(\frac{4}{12}\)) ≈ 36.87°
Let \(m \widehat{D E}\) be x.
\(\frac{\left(360^{\circ} – x\right) – x}{2}\) = 36.87°
x = 143.13°
Therefore, \(m \widehat{D E}\) = 143.13°, and the area is 48 square units .
Question 7.
Find the measure of \(\widehat{B G}\), \(\widehat{F B}\), and \(\widehat{G F}\).
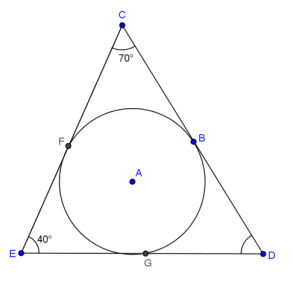
Answer:
\(m \widehat{B G}\) =\(m \widehat{F B}\) = 110°, \(m \widehat{F G}\) = 140°
Question 8.
Find the values of x and y.
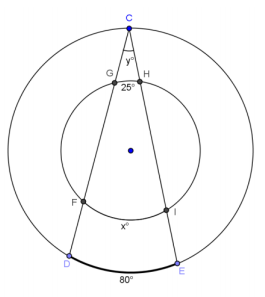
Answer:
x = 105, y = 40
Question 9.
The radius of a circle is 6.
a. If the angle formed between two tangent lines to the circle is 60°, how long is the segment between the point of intersection of the tangent lines and the center of the circle?
Answer:
10.39
b. If the angle formed between the two tangent lines is 120°, how long are each of the segments between the point of intersection of the tangent lines and the point of tangency? Round to the nearest hundredth.
Answer:
\(\frac{6}{\sqrt{3}}\) ≈ 3.46
Question 10.
\(\overline{D C}\) and \(\overline{E C}\) are tangent to circle A. Prove BD = BE.
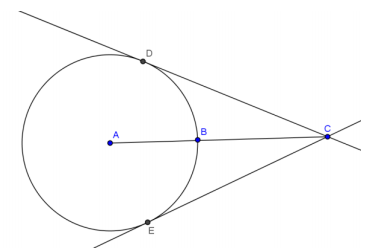
Aanswer:
Join \(\overline{A D}\), \(\overline{A E}\), \(\overline{B D}\), and \(\overline{B E}\).
AD = AE Radii of same circle
AC = AC Reflexive Property
m∠ADC = m∠AEC = 90° Radii perpendicular to tangent lines at point of tangency
△ADC and △AEC are right triangles Definition of right triangle
△ADC ≅ △AEC HL
m∠CAE = m∠CAD Corresponding angles of congruent triangles are equal in measure.
\(\widehat{B D}\) ≅ \(\widehat{B E}\) Congruent angles intercept congruent arcs.
BD = BE Congruent arcs intercept chords of equal measure.
Eureka Math Geometry Module 5 Lesson 15 Exit Ticket Answer Key
Question 1.
Find x. Explain your answer.
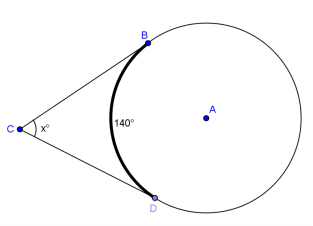
Answer:
x = 40. Major arc \(m \widehat{B D}\) = 360 – 140 = 220.
Question 2.
Use the diagram to show that \(m \widehat{D E}\) = y° + x° and \(m \widehat{F G}\) = y° – x°. Justify your work.
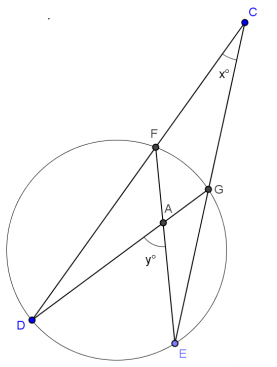
Answer:
x = \(\frac{1}{2}\) \(m \widehat{D E}\) – \(m \widehat{F G}\), or 2x = \(m \widehat{D E}\) – \(m \widehat{F G}\). Angle whose vertex lies exterior of circle is equal to half the difference of the angle measures of its larger and smaller intercepted arcs.
y = \(\frac{1}{2}\) \(m \widehat{D E}\) + \(m \widehat{F G}\), or 2y = \(m \widehat{D E}\) + \(m \widehat{F G}\). Angle whose vertex lies in a circle is equal to half the sum of the arcs intercepted by the angle and its vertical angle.
Adding the two equations gives 2x + 2y = 2m, or
x + y = \(m \widehat{D E}\).
Subtracting the two equations gives 2y – 2x = 2\(m \widehat{F G}\), or
y – x = \(m \widehat{F G}\).