Engage NY Eureka Math Geometry Module 5 Lesson 14 Answer Key
Eureka Math Geometry Module 5 Lesson 14 Example Answer Key
Example
a. Find x. Justify your answer.
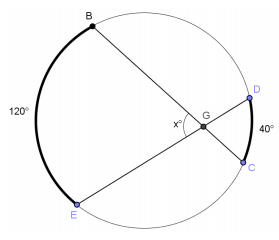
Answer:
80°. If you draw △BDG, m∠DBG = 20° and m∠BDG = 60° because they are half of the measures of their inscribed arcs. That means m∠BGD = 100° because the sums of the angles of a triangle total 180°. ∠DGB and ∠BGE are supplementary, so m∠BGE = 80°.
b. Find x.
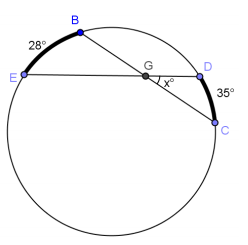
Answer:
31.5°
Eureka Math Geometry Module 5 Lesson 14 Exercise Answer Key
Opening Exercise
\(\overleftrightarrow{D B}\) is tangent to the circle as shown.
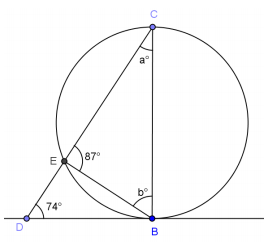
a. Find the values of a and b.
a = 13, b = 80
b. Is \(\overline{C B}\) a diameter of the circle? Explain.
Answer:
No, if \(\overline{C B}\) was a diameter, then m∠CEB would be 90°.
Exercises 1–2
Exercise 1.
In circle P, \(\overline{P O}\) is a radius, and \(m \widehat{M O}\) = 142°. Find m∠MOP, and explain how you know.
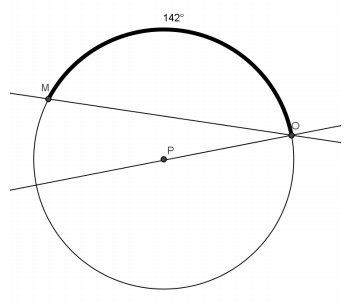
Answer:
m∠MOP = 19°
Since \(\overline{P O}\) is a radius and extends to a diameter, the measure of the arc intercepted by the diameter is 180°. \(m \widehat{M O}\) = 142°, so the arc intercepted by ∠MOP is 180° – 142° or 38°. ∠MOP is inscribed in this arc, so its measure is half the degree measure of the arc or \(\frac{1}{2}\) (38°) = 19°.
Exercise 2.
In the circle shown, \(m \widehat{C E}\) = 55°. Find m∠DEF and \(m \widehat{E G}\). Explain your answer.
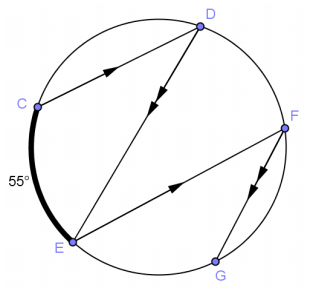
Answer:
m∠DEF = 27.5°
\(m \widehat{E G}\) = 55°
\(m \widehat{C E}\) = \(m \widehat{D F}\) and \(m \widehat{D F}\) = \(m \widehat{E G}\) because arcs between parallel lines are equal in measure.
By substitution, \(m \widehat{E G}\) = 55°.
\(m \widehat{D F}\) = 55°, so m∠DEF = \(\frac{1}{2}\) (55°) = 27.5° because it is inscribed in a 55° arc.
Exercises 3–7
In Exercises 3–5, find x and y.
Exercise 3.
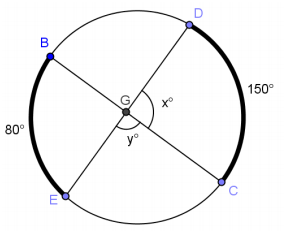
Answer:
x = 115, y = 65
Exercise 4.
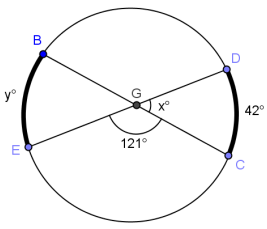
Answer:
x = 59, y = 76
Exercise 5.
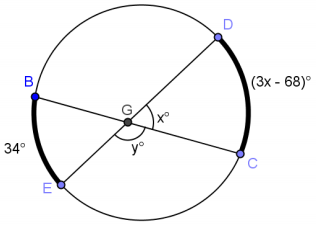
Answer:
x = 34, y = 146
Exercise 6.
In the circle shown, \(\overline{B C}\) is a diameter. Find x and y.
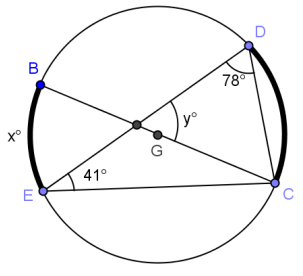
Answer:
x = 24, y = 53
Exercise 7.
In the circle shown, \(\overline{B C}\)is a diameter. DC:BE = 2:1. Prove y = 180 – \(\frac{3}{2}\) x using a two – column proof.
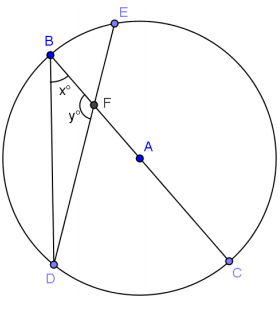
Answer:
\(\overline{B C}\) is a diameter of circle A Given
m∠DBC = x° Given
\(m \widehat{D C}\) = 2x° Arc is double angle measure of inscribed angle
\(m \widehat{B E}\) = x° DC : BE = 2 : 1
\(m \widehat{B D C}\) = \(m \widehat{B E C}\) = 180° Semicircle measures 180°
\(m \widehat{D C}\) = 180° – 2x° Arc addition
\(m \widehat{E C}\) = 180° – x° Arc addition
m∠BFD = \(\frac{1}{2}\)(180° – 2x° + 180° – x°) Measure of angle whose vertex lies in a circle is half the angle measures of arcs intercepted by it and its vertical angles
y° = 180° – \(\frac{3}{2}\) x° Substitution and simplification
Eureka Math Geometry Module 5 Lesson 14 Problem Set Answer Key
In Problems 1–4, find x.
Question 1.
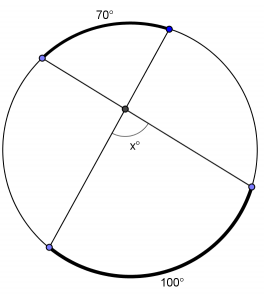
Answer:
x = 85
Question 2.
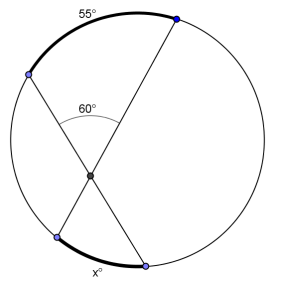
Answer:
x = 65
Question 3.
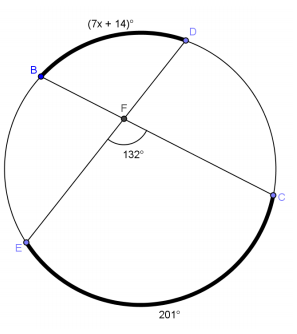
Answer:
x = 7
Question 4.
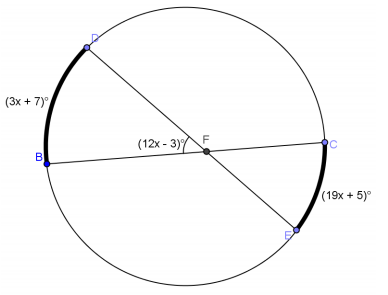
Answer:
x = 9
Question 5.
Find x (\(m \widehat{C E}\)) and y (\(m \widehat{D G}\)).
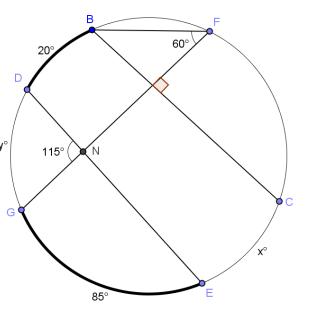
Answer:
60 = \(\frac{1}{2}\)(y + 20)
\(\frac{x + (85 + x)}{2}\) = 90
x = 70, y = 100
Question 6.
Find the ratio of \(m \widehat{E C}\) : \(m \widehat{D B}\).
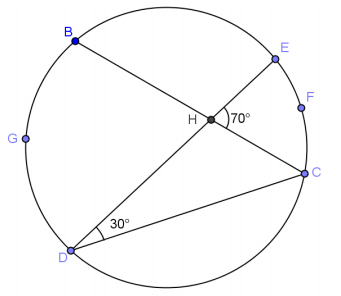
Answer:
3:4
Question 7.
\(\overline{B C}\) is a diameter of circle A. Find x.
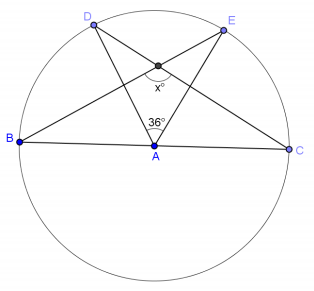
Answer:
x = 108
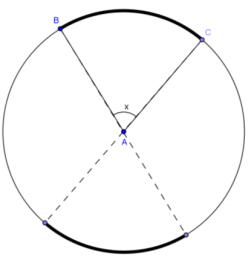
Question 8.
Show that the general formula we discovered in Example 1 also works for central angles. (Hint: Extend the radii to form two diameters, and use relationships between central angles and arc measure.)
Answer:
Extend the radii to form two diameters.
Let the measure of the central angle be equal to x°.
The measure \(\widehat{B C}\) = x° because the angle measure of the arc intercepted by a central angle is equal to the measure of the central angle.
The measure of the vertical angle is also x° because vertical angles are congruent.
The angle of the arc intercepted by the vertical angle is also x°.
The measure of the central angle is half the sum of the angle measures of the arcs intercepted by the central angle and its vertical angle.
x = \(\frac{1}{2}\) (x + x)
This formula also works for central angles.
Eureka Math Geometry Module 5 Lesson 14 Exit Ticket Answer Key
Question 1.
Lowell says that m∠DFC = \(\frac{1}{2}\) (123) = 61° because it is half of the intercepted arc. Sandra says that you cannot determine the measure of ∠DFC because you do not have enough information. Who is correct and why?
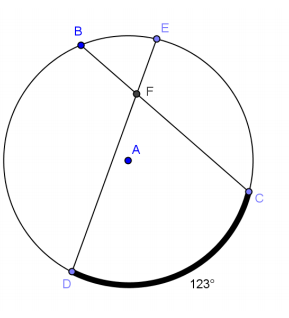
Answer:
Sandra is correct. We would need more information to determine the answer. Lowell is incorrect because ∠DFC is not an inscribed angle.
Question 2.
If m∠EFC = 9°, find and explain how you determined your answer.
a. m∠BFE
Answer:
81°, m∠EFC + m∠BFE = 180° (supplementary angles), so 180° – 99° = m∠BFE.
b. \(m \widehat{B E}\)
Answer:
39°, 81° = \(\frac{1}{2}\)(\(m \widehat{B E}\) + 123°) using the formula for an angle with vertex inside a circle.