Eureka Math Geometry Module 5 Lesson 11 Answer Key

Engage NY Eureka Math Geometry Module 5 Lesson 11 Answer Key

Eureka Math Geometry Module 5 Lesson 11 Exercise Answer Key

Exercises
Exercise 1.
\(\overline{C D}\) and \(\overline{C E}\) are tangent to circle A at points D and E, respectively. Use a two-column proof to prove a = b.

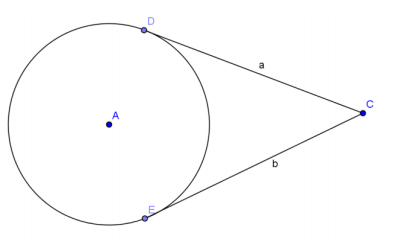
Answer:
Draw radii \(\overline{A D}\) and \(\overline{A E}\)and segment \(\overline{A C}\).
CD = a, CE = b Given
∠ADC and ∠AEC are right angles. Tangent lines are perpendicular to the radius at the point of tangency.
△ADC and △AEC are right triangles. Definition of a right triangle
AD = AE Radii of the same circle are equal in measure.
AC = AC Reflexive property
△ADC ≅ △AEC HL
CD = CE Corresponding sides of congruent triangles are equal in length.
a = b Substitution

Exercise 2.
In circle A, the radius is 9 mm and BC = 12 mm.

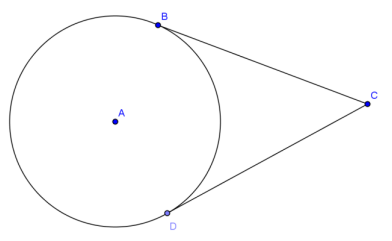
a. Find AC.
Answer:
AC = 15 mm

b. Find the area of △ACD.
Answer:
A = 54 mm²

c. Find the perimeter of quadrilateral ABCD.
Answer:
P = 42 mm

Exercise 3.
In circle A, EF = 12 and AE = 13. AE : AC = 1 : 3.

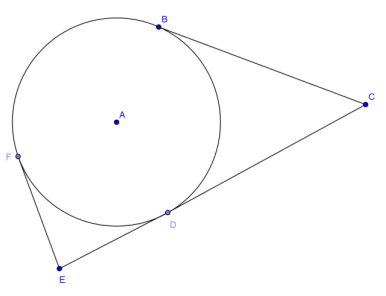
a. Find the radius of the circle.
Answer:
5

b. Find BC (round to the nearest whole number).
Answer:
39

c. Find EC.
Answer:
51

Eureka Math Geometry Module 5 Lesson 11 Problem Set Answer Key

Question 1.
If AB = 5, BC = 12, and AC = 13, is \(\overleftrightarrow{B C}\) tangent to circle A at point B? Explain.

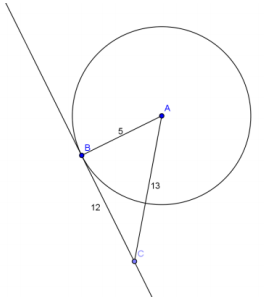
Answer:
Yes. △ABC is a right triangle because the Pythagorean theorem holds: 5² + 12² = 13². Angle B is right, so \(\overleftrightarrow{B C}\) is tangent to circle A at point B.

Question 2.
\(\overleftrightarrow{B C}\) is tangent to circle A at point B. DC = 9 and BC = 15.

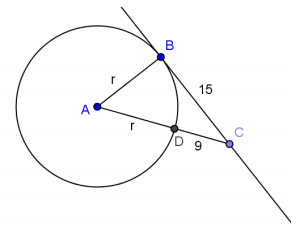
a. Find the radius of the circle.
Answer:
r = 8

b. Find AC.
Answer:
AC = 17

Question 3.
A circular pond is fenced on two opposite sides (\(\overline{C D}\), \(\overline{F E}\)) with wood and the other two sides with metal fencing.
If all four sides of fencing are tangent to the pond, is there more wood or metal fencing used?

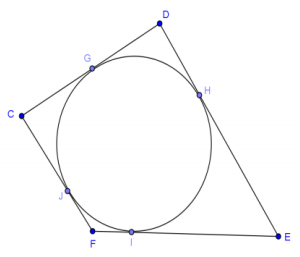
Answer:
There is an equal amount of wood and metal fencing because the distance from each corner to the point of tangency is the same.

Question 4.
Find x if the line shown is tangent to the circle at point B.

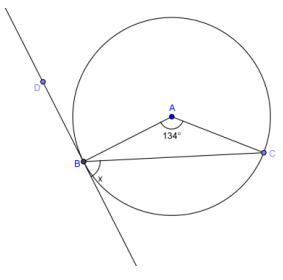
Answer:
67°

Question 5.
\(\overleftrightarrow{P C}\) is tangent to the circle at point C, and CD = DE.

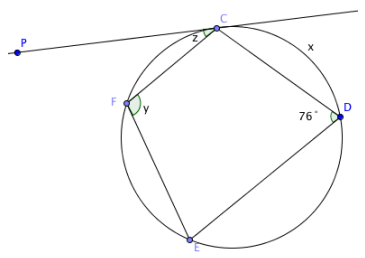
a. Find x (\(m \widehat{C D}\)).
Answer:
∠CDE is an inscribed angle, so \(m \widehat{C F E}\) is two times the measure of the intercepted arc; \(m \widehat{C F E}\) = 152° and \(m \widehat{C D E}\) = 208°. Since CD = DE, then \(m \widehat{C D}\) = m \(\widehat{D E}\). Therefore, 2x = 208° and x = 104°.

b. Find y (m∠CFE).
Answer:
\(m \widehat{C D E}\) = 208°, so m∠CFE must be one half this value since it is an inscribed angle that intercepts the arc. Therefore, y = 104°.

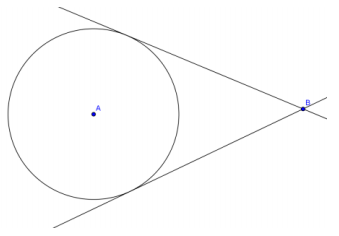
Question 6.
Construct two lines tangent to circle A through point B.

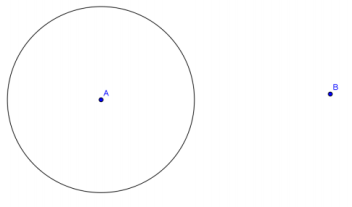
Answer:

Question 7.
Find x, the length of the common tangent line between the two circles (round to the nearest hundredth).

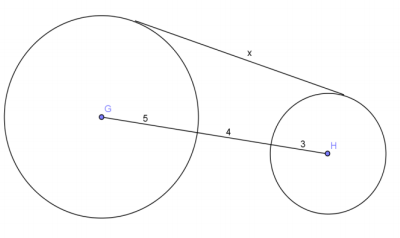
Answer:

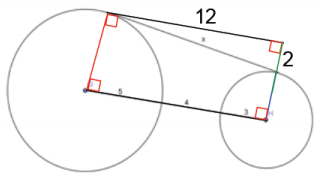
x = 12.17

Question 8.
\(\overline{E F}\) is tangent to both circles A and C. The radius of circle A is 9, and the radius of circle C is 5. The circles are 2 units apart. Find the length of \(\overline{E F}\), or x (round to the nearest hundredth).

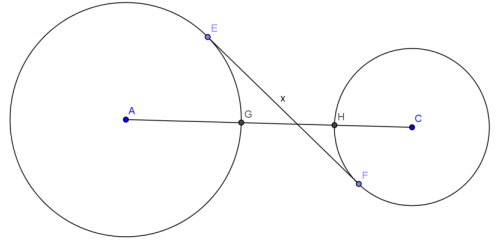
Answer:
Draw radius \(\overline{A E}\) and radius \(\overline{C F}\). Label the intersection of \(\overline{E F}\) and \(\overline{A C}\) as Z.

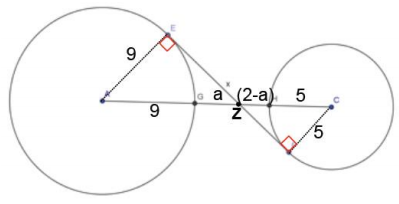
Triangles AEZ and CFZ are similar since both have right angles (∠E and ∠F) and a pair of vertical angles equal in measure (∠AZE and ∠CZF).
\(\frac{AZ}{AE}\) = \(\frac{CZ}{CF}\)
\(\frac{9}{5}\) = \(\frac{9 + a}{7-a}\)
a = \(\frac{9}{7}\)
EZ = \(\sqrt{\left(9 + \frac{9}{7}\right)^{2}-9^{2}}\)
ZF = \(\sqrt{\left(5 + \frac{5}{7}\right)^{2}-5^{2}}\)
EF = EZ + ZF
EF = \(\sqrt{\left(9 + \frac{9}{7}\right)^{2}-9^{2}} + \sqrt{\left(5 + \frac{5}{7}\right)^{2}-5^{2}}\)
EF ≈ 7.75
The length of \(\overline{E F}\), or x, is approximately 7.75 units.

Eureka Math Geometry Module 5 Lesson 11 Exit Ticket Answer Key

Question 1.
If BC = 9, AB = 6, and AC = 15, is \(\overleftrightarrow{B C}\) tangent to circle A? Explain.

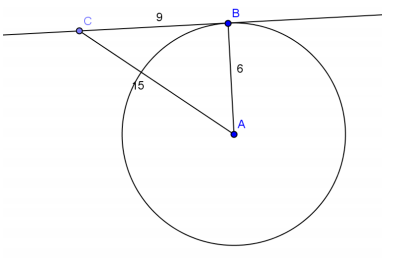
Answer:
No. △ABC is not a right triangle because 9² + 6² ≠ 15². This means \(\overline{A B}\) is not perpendicular to \(\overline{B C}\).

Question 2.
Construct a line tangent to circle A through point B.

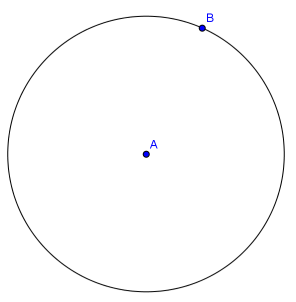
Answer:
Answers will vary.