Engage NY Eureka Math Geometry Module 5 Lesson 10 Answer Key
Eureka Math Geometry Module 5 Lesson 10 Exercise Answer Key
Opening Exercise
In the following figure, a cylinder is carved out from within another cylinder of the same height; the bases of both cylinders share the same center.
a. Sketch a cross section of the figure parallel to the base.
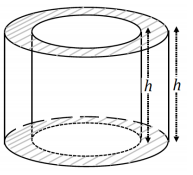
Answer:
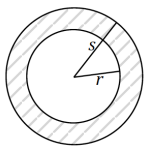
b. Mark and label the shorter of the two radii as r and the longer of the two radii as s.
Show how to calculate the area of the shaded region, and explain the parts of the expression.
Answer:
Area(shaded) = π(s2 – r2)
Where s represents radius of outer circle and r represents the radius of inner circle.
Exercises
Exercise 1.
Find the area of the following annulus.
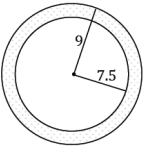
Answer:
Area(shaded) = π(92 – 7.52)
Area(shaded) = 24.75π
The area of the annulus is 24.75π units2.
Exercise 2.
The larger circle of an annulus has a diameter of 10 cm, and the smaller circle has a diameter of 7.6 cm. What is the area of the annulus?
Answer:
The radius of the larger circle is 5 cm, and the radius of the smaller circle is 3.8 cm.
Area(shaded) = π(52 – 3.82)
Area(shaded) = 10.56π
The area of the annulus is 10.56π cm2.
Exercise 3.
In the following annulus, the radius of the larger circle is twice the radius of the smaller circle. If the area of the following annulus is 12π units2, what is the radius of the larger circle?
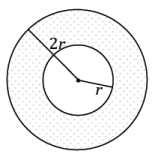
Answer:
Area(shaded):
π((2r)2 – r2) = 12π
3r2 = 12
r = 2
The radius of the larger circle is twice the radius of the smaller circle, or 2(2) = 4; therefore, the radius of the larger circle is 4 units.
Exercise 4.
An ice cream shop wants to design a super straw to serve with its extra thick milkshakes that is double both the width and thickness of a standard straw. A standard straw is 4 mm in diameter and 0.5 mm thick.
a. What is the cross – sectional (parallel to the base) area of the new straw (round to the nearest hundredth)?
Answer:
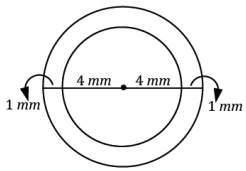
Super straw diameter, including straw thickness:
(8 + 1 + 1) mm = 10 mm
Super straw diameter, not including straw thickness: 8 mm
Cross – sectional area: π((5 mm)2 – (4 mm)2 ) = 28.27 mm2
b. If the new straw is 10 cm long, what is the maximum volume of milkshake that can be in the straw at one time (round to the nearest hundredth)?
Answer:
Maximum volume:
(50.27 mm2 )(10 cm⋅\(\frac{10 mm}{1 cm}\)) = 5027 mm3
c. A large milkshake is 32 fl.oz. (approximately 950 mL). If Corbin withdraws the full capacity of a straw 10 times a minute, what is the minimum amount of time that it will take him to drink the milkshake (round to the nearest minute)?
Answer:
950 mL = 950 000 mm3
Volume consumed in 1 minute:
(5027 mm3 )(10/(1 min)) = 50270 mm3/min
Time needed to finish 32 fl.oz.:
\(\frac{950000 \mathrm{~mm}^{3}}{50270 \frac{\mathrm{mm}^{3}}{\mathrm{~min}}}\) = 18.90 min.
It will take him approximately 19 minutes to drink the milkshake.
Exercise 5.
In the circle given, \(\overline{E D}\) is the diameter and is perpendicular to chord \(\overline{C B}\). DF = 8 cm, and FE = 2 cm. Find AC, BC, m∠CAB, the arc length of \(\widehat{C E B}\), and the area of sector CAB (round to the nearest hundredth, if necessary).
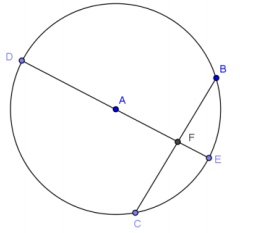
Answer:
AC = 5 cm
BC = 8 cm
m∠CAB = 2(53.13°) = 106.26°
arc length \(\widehat{C E B}\) = 9.27 cm
area of sector CEB = 23.18 cm2
Exercise 6.
Given circle A with ∠BAC≅∠BAD, find the following (round to the nearest hundredth, if necessary).
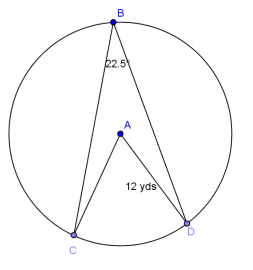
a. \(m\widehat{C D}\)
Answer:
45°
b. \(m\widehat{C B D}\)
Answer:
315°
c. \(m\widehat{B C D}\)
Answer:
202.5°
d. Arc length \(\widehat{C D}\)
Answer:
9.42 yd.
e. Arc length \(m = \widehat{C B D}\)
Answer:
65.98 yd.
f. Arc length \(\widehat{B C D}\)
Answer:
42.41 yd.
g. Area of sector CAD
Answer:
56.55 yd2
Exercise 7.
Given circle A, find the following (round to the nearest hundredth, if necessary).
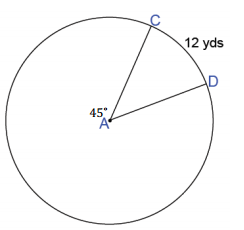
a. Circumference of circle A
Answer:
96 yd.
b. Radius of circle A
Answer:
15.28 yd.
c. Area of sector CAD
Answer:
91.69 yd2
Exercise 8.
Given circle A, find the following (round to the nearest hundredth, if necessary).
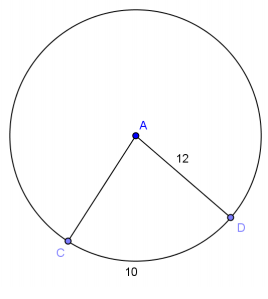
a. m∠CAD
Answer:
47.75°
b. Area of sector CD
Answer:
60 units2
Exercise 9.
Find the area of the shaded region (round to the nearest hundredth).
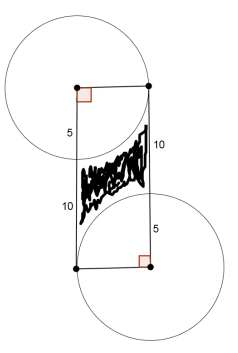
Answer:
(5)(15) – \(\frac{25\pi}{2}\) = 35.73
The area is 35.73 units2.
Exercise 10.
Many large cities are building or have built mega Ferris wheels. One is 600 feet in diameter and has 48 cars each seating up to 20 people. Each time the Ferris wheel turns θ degrees, a car is in a position to load.
a. How far does a car move with each rotation of θ degrees (round to the nearest whole number)?
Answer:
distance = (300)(\(\frac{2\pi}{48}\))ft. ≈ 39 ft.
b. What is the value of θ in degrees?
Answer:
\(2\frac{\pi}{48}\) (\(\frac{180^{\circ}}{\pi}\)) = 7.5°
Exercise 11.
△ABC is an equilateral triangle with edge length 20 cm. D, E, and F are midpoints of the sides. The vertices of the triangle are the centers of the circles creating the arcs shown. Find the following (round to the nearest hundredth).
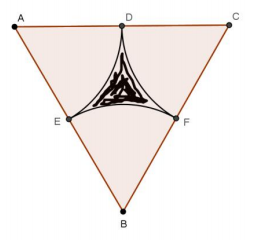
a. Area of the sector with center A
Answer:
52.36 cm2
b. Area of △ABC
Answer:
173.21 cm2
c. Area of the shaded region
Answer:
16.13 cm2
d. Perimeter of the shaded region
Answer:
31.42 cm
Exercise 12.
In the figure shown, AC = BF = 5 cm, GH = 2 cm, and m∠HAI = 30°. Find the area inside the rectangle but outside of the circles (round to the nearest hundredth).
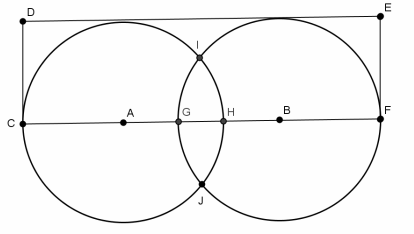
Answer:
Shaded Area = Area(sector AIH) – Area(△AIH)
Area(sector AIH): \(25\frac{\pi}{12}\)
Area(△AIH): \(\frac{1}{2}\) (5 cos30 )(5 sin30 )
Shaded Area: \(25\frac{\pi}{12}\) – \(\frac{1}{2}\) (5 cos 30)(5 sin 30)
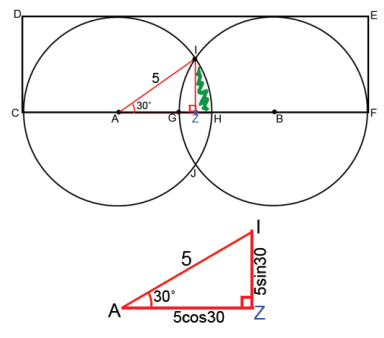
Area defined by the overlap of the circles:
2[2(Shaded Area)]
Half of the overlapping area of the circles (bound by G, H, and I):
2(Shaded Area), or
2[\(25\frac{\pi}{12}\) – \(\frac{1}{2}\) (5 cos30 )(5 sin30 )]
Area of rectangle: (CD)(CF)
CD = 5
CF = CH + GF – GH = 10 + 10 – 2(5 – 5 cos30 )
Area = Area(rectangle) – Area(outside circles)
Area = [(5)(20 – 2(5 – 5 cos30))] – [25π – 2[[\(25\frac{\pi}{12}\)[\(25\frac{\pi}{12}\) – \(\frac{1}{2}\) (5 cos30 )(5 sin30 )]]
Area ≈ 17.03
The area inside the rectangle but outside the circles is approximately 17.03 cm2.
Exercise 13.
This is a picture of a piece of a mosaic tile. If the radius of each smaller circle is 1 inch, find the area of the red section, the white section, and the blue section (round to the nearest hundredth).
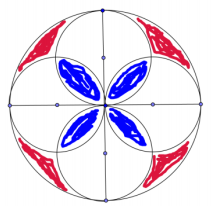
Answer:
Area(Blue): 8(\(\frac{\pi}{4}\) – \(\frac{1}{2}\)) = 2π – 4
Area(Red): 4[2(\(\frac{\pi}{2}\)) – 2(π/4 – \(\frac{1}{2}\))] = 2π – 4
Area(White): 4π – 2(2π – 4) = 8
The blue section has an area of approximately 2.28 in2, the red section has an area of approximately 2.28 〖in〗2, and the white section has an area of 8 in2.
Eureka Math Geometry Module 5 Lesson 10 Problem Set Answer Key
Question 1.
Find the area of the shaded region if the diameter is 32 inches (round to the nearest hundredth).
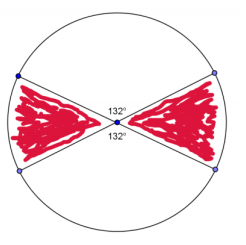
Answer:
214.47 in2
Question 2.
Find the area of the entire circle given the area of the sector.
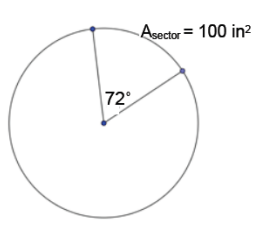
Answer:
500 in2
Question 3.
\(m \widehat{D F}\) and \(m \widehat{B G}\) are arcs of concentric circles with \(\overline{B D}\) and \(\overline{F G}\) lying on the radii of the larger circle. Find the area of the region (round to the nearest hundredth).
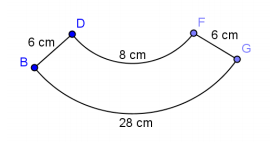
Answer:
(1) 8 = x(θ); θ = \(\frac{8}{x}\)
(2) 28 = (x + 6)(θ)
28 = (x + 6)(\(\frac{8}{x}\))
x = 2.4
Substituting into (1):
8 = (2.4)(θ)
θ = \(\frac{10}{3}\)
Area of annulus:
π(8.42 – 2.42 ) = 64.8π
Area of region:
(\(\frac{\frac{10}{3}}{2 \pi}\))(64.8π) = 108
The area of the region is 108 cm2.
Question 4.
Find the radius of the circle as well as x, y, and z (leave angle measures in radians and arc length in terms of pi). Note that C and D do not lie on a diameter.
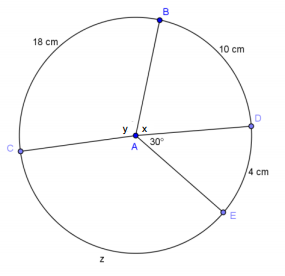
Answer:
Let r be defined as the radius.
4 = r(\(\frac{\pi}{6}\)); r = \(\frac{24}{\pi}\)
\(\frac{24}{\pi}\) (x) = 10; x = \(\frac{5\pi}{12}\)
\(\frac{24}{\pi}\) (y) = 18; y = \(\frac{3\pi}{4}\)
m∠CAE must be \(\frac{2\pi}{3}\). Then,
z = \(\frac{24}{\pi}\) (\(\frac{2\pi}{3}\)) = 16
r = \(\frac{24}{\pi}\) cm
x = \(\frac{5\pi}{12}\)
y = \(\frac{3\pi}{4}\)
z = 16 cm
Question 5.
In the figure, the radii of two concentric circles are 24 cm and 12 cm. \(m \widehat{D A C}\) = 120°. If a chord \(\overline{D E}\) of the larger circle intersects the smaller circle only at C, find the area of the shaded region in terms of π.
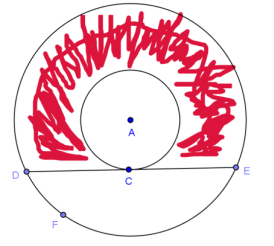
Answer:
Area of complete annulus:
(242 – 122 )π = 432π
Area of dotted region:
\(\frac{576\pi}{3}\) – (\(\frac{1}{2}\))(12)(24\(\sqrt{3}\)) = 192π – 144\(\sqrt{3}\)
Area of shaded region:
432π – (192π – 144\(\sqrt{3}\)) = 240π + 144\(\sqrt{3}\)
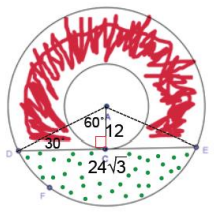
The area of the shaded region is (240π + 144\(\sqrt{3}\)) cm2.
Eureka Math Geometry Module 5 Lesson 10 Exit Ticket Answer Key
Question 1.
Given circle A, find the following (round to the nearest hundredth).
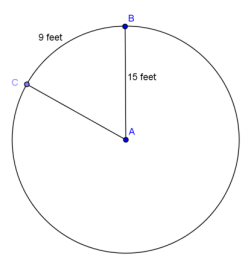
a. \(m \widehat{B C}\) in degrees
Answer:
34.38°
b. Area of sector BAC
Answer:
67.5 ft2
Question 2.
Find the shaded area (round to the nearest hundredth).
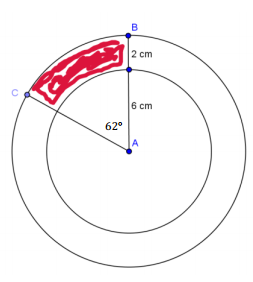
Answer:
15.15 cm2