Eureka Math Geometry Module 4 Lesson 8 Answer Key

Engage NY Eureka Math Geometry Module 4 Lesson 8 Answer Key

Eureka Math Geometry Module 4 Lesson 8 Example Answer Key

Example 2.
a. What is the relationship between two coplanar lines that are perpendicular to the same line?
Answer:
Have students draw a line and label it k. Students then construct line
l₁ perpendicular to line k. Finally, students construct line l₂ not coincident with line 1, also perpendicular to line k.

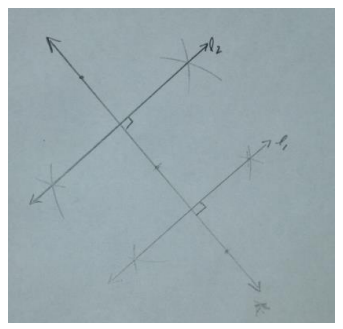
→ What can we say about the relationship between lines l₁ and l₂?
These lines are parallel because the corresponding angles that are created by the transversal k are congruent.

→ If the slope of line k is m, what is the slope of l₁? Support your answer. (Lesson 5)
The slope of l₁ is –\(\frac{1}{m}\) because the slopes of perpendicular lines are negative reciprocals of each other.

→ If the slope of line k is m, what is the slope of l₂? Support your answer. (Lesson 5)
The slope of l₂ is \(\frac{1}{m}\) because the slopes of perpendicular lines are negative reciprocals of each other.

→ Using your answers to the last two questions, what can we say about the slopes of lines l₁ and l₂?
l₁ and l₂ have equal slopes.

→ What can be said about l₁ and l₂ if they have equal slopes?
l₁ and l₂ are parallel.

→ What is the relationship between two coplanar lines that are perpendicular to the same line?
If two lines are perpendicular to the same line, then the two lines are parallel, and if two lines are parallel, then their slopes are equal.

→ Restate this to your partner in your own words, and explain it by drawing a picture.

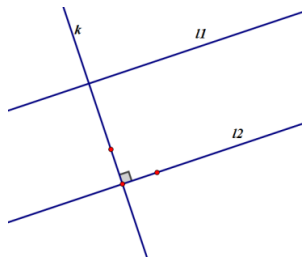
b. Given two lines, l₁ and l₂, with equal slopes and a line k that is perpendicular to one of these two parallel lines, l₁:
i. What is the relationship between line k and the other line, l₂?
ii. What is the relationship between l₁ and l₂?
Answer:

Eureka Math Geometry Module 4 Lesson 8 Exercise Answer Key

Exercise 1.
a. Write an equation of the line that passes through the origin and intersects the line 2x + 5y = 7 to form a right angle.
Answer:
y = \(\frac{5}{2}\)x

b. Determine whether the lines given by the equations 2x + 3y = 6 and y = \(\frac{3}{2}\)x + 4 are perpendicular. Support your answer.
Answer:
The slope of the first line is –\(\frac{2}{3}\), and the slope of the second line is \(\frac{3}{2}\). The product of these two slopes is – 1; therefore, the two lines are perpendicular.

c. Two lines having the same y-intercept are perpendicular. If the equation of one of these lines is y = –\(\frac{4}{5}\)x + 6, what is the equation of the second line?
Answer:
y = \(\frac{5}{4}\)x + 6

Exercise 2.
Given a point (- 3, 6) and a line y = 2x – 8:
a. What is the slope of the line?
Answer:
2

b. What is the slope of any line parallel to the given line?
Answer:
2

c. Write an equation of a line through the point and parallel to the line.
Answer:
2x – y = -12

d. What is the slope of any line perpendicular to the given line? Explain.
Answer:
The slope is –\(\frac{1}{2}\); perpendicular lines have slopes that are negative reciprocals of each other.

Exercise 3.
Find an equation of a line through (0, – 7) and parallel to the line y = \(\frac{1}{2}\)x + 5.
a. What is the slope of any line parallel to the given line? Explain your answer.
Answer:
The slope is \(\frac{1}{2}\) lines are parallel if and only if they have equal slopes.

b. Write an equation of a line through the point and parallel to the line.
Answer:
x – 2y = 14

c. If a line is perpendicular to y = \(\frac{1}{2}\)x + 5, will it be perpendicular to x – 2y = 14? Explain.
Answer:
If a line is perpendicular to y = \(\frac{1}{2}\)x + 5, it will also be perpendicular to y = \(\frac{1}{2}\)x – 7 because a line perpendicular to one line is perpendicular to all lines parallel to that line.

Exercise 4.
Find an equation of a line through (√3, \(\frac{1}{2}\)) parallel to the line:
a. x = – 9
Answer:
x = √3

b. y = -√7
Answer:
y = \(\frac{1}{2}\)

c. What can you conclude about your answer in parts (a) and (b)?
Answer:
They are perpendicular to each other. x = √3 is a vertical line, and y = \(\frac{1}{2}\) is a horizontal line.

Exercise 5.
Find an equation of a line through (-√2, π) parallel to the line x – 7y = √5.
Answer:
x – 7y = -√2 – 7π

Exercise 6.
Recall that our search robot is moving along the line y = 3x – 600 and wishes to make a right turn at the point (400, 600). Find an equation for the perpendicular line on which the robot is to move. Verify that your line intersects the x-axis at (2200, 0).
Answer:
x + 3y = 2200; when y = 0, x = 2200

Exercise 7.
A robot, always moving at a constant speed of 2 units per second, starts at position (20, 50) on the coordinate plane and heads In a southeast direction along the line 3x + 4y = 260. After 15 seconds, It turns clockwise 900 and travels in a straight line in this new direction.

a. What are the coordinates of the point at which the robot made the turn? What might be a relatively straightforward way of determining this point?
Answer:
The coordinates are (44, 32). We know the robot moves down 3 units and right 4 units, and the distance moved in 15 seconds is 30 units. This gives us a right triangle with hypotenuse 5, so we need to move this way 6 times. From (20, 50), move a total of down 18 units and right 24 units.

b. Find an equation for the second line on which the robot traveled.
Answer:
4x – 3y = 80

c. If, after turning, the robot travels for 20 seconds along this line and then stops, how far will it be from its starting position?
Answer:
It will be at the point (20, 0), 50 units from its starting position.

d. What is the equation of the line the robot needs to travel along in order to now return to its starting position? How long will It take for the robot to get there?
Answer:
x = 20; 25 seconds

Eureka Math Geometry Module 4 Lesson 8 Problem Set Answer Key

Question 1.
Write the equation of the line through (-5, 3) and:
a. Parallel to x = -1.
Answer:
x = – 5

b. Perpendicular to x = -1.
Answer:
y = 3

c. Parallel to y = x + 2.
Answer:
3x – 5y = -30

d. Perpendicular to y = \(\frac{3}{5}\)x + 2.
Answer:
5x + 3y = -16

Question 2.
Write the equation of the line through (√3, \(\frac{5}{4}\)) and:
a. Parallel to y = 7.
y = \(\frac{5}{4}\)

b. Perpendicular to y = 7.
Answer:
x = √3

c. Parallel to \(\frac{1}{2}\)x – \(\frac{3}{4}\)y = 10.
Answer:
8x – 12y = – 15 + 8√3

d. Perpendicular to \(\frac{1}{2}\)x – \(\frac{3}{4}\)y = 10.
Answer:
6x + 4y = 5 + 6√3

Question 3.
A vacuum robot is in a room and charging at position (0, 5). Once charged, it begins moving on a northeast path at a constant speed of \(\frac{1}{2}\) foot per second along the line 4x – 3y = – 15. After 60 seconds, It turns right 900 and travels in the new direction.
a. What are the coordinates of the point at which the robot made the turn?
Answer:
(18, 29)

b. Find an equation for the second line on which the robot traveled.
Answer:
3x + 4y = 170

c. If after turning, the robot travels 80 seconds along this line, what is the distance between the starting position and the robot’s current position?
Answer:
50 feet

d. What is the equation of the line the robot needs to travel along in order to return and recharge? How long will It take the robot to get there?
Answer:
y = 5; 100 seconds

Question 4.
Given the statement is parallel to construct an argument for or against this statement using the two triangles shown.

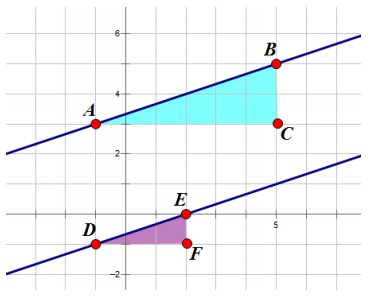
Answer:

Question 5.
Recall the proof we did in Example 1: Let l₁ and l₂ be two non-vertical lines in the Cartesian plane. l₁ and l₂ are perpendicular If and only if their slopes are negative reciprocals of each other. In class, we looked at the case where both y-intercepts were not zero. In Lesson 5, we looked at the case where both y-intercepts were equal to zero, when the vertex of the right angle was at the origin. Reconstruct the proof for the case where one line has a y-intercept of zero, and the other line has a nonzero y-lntercept.
Answer:
Suppose l₁ passes through the origin; then, It will be given by the equation y = m₁x, and l₂is given by the equation y = m₂x + b₂. Here, we are assuming m₁, m₂, and b₂ are not zero. We can still use the same two points on l₂ as we used in Example 1, (0, b₂) and absent or who (1, m₂ + b₂). We will have to find an additional point to use on l₁, as the x- and y- intercepts are the same point because this line passes through the origin, (0, 0). Let’s let our second point be (1, m₁).
If l₁ ⊥ l₂ then:
(1 – 0) (1 – 0) + (m₂ – 0) (b₂ – 0) = 0
1 + m₁m₂ = 0
1 = – m₁m₂
–\(\frac{1}{m_{1}}\) = m2

Question 6.
Challenge: Reconstruct the proof we did in Example 1 if one line has a slope of zero.
Answer:
If m₁ = 0, then 1 is given by the equation y = b₁, and l₂ is given by the equation y = m₂x + b₂. Here we are assuming m₂, b₁, and b₂ are not zero.
Choosing the points (0, b₁) and (1, b₁) on l₁ and (0, b₂) and (1, m₂ + b₂) on l₂,
If 1₁ ⊥ l₂, then:
(1 – 0) (1 – 0) + (b₁ – b₁) (m₂ + b₂ – b₂) = 0
1 + 0 = 0
1 = 0
This is a false statement. If one of the perpendicular lines is horizontal, their slopes cannot be negative reciprocals.

Eureka Math Geometry Module 4 Lesson 8 Exit Ticket Answer Key

Question 1.
Are the pairs of lines parallel, perpendicular, or neither? Explain.
a. 3x + 2y = 74 and 9x – 6y = 15
Answer:
The lines are neither, and the slopes are –\(\frac{3}{2}\) and \(\frac{3}{2}\)

b. 4x – 9y = 8 and 18x + 8y = 7
Answer:
The lines are perpendicular, and the slopes are \(\frac{4}{9}\) and –\(\frac{9}{4}\).

Question 2.
Write the equation of the line passing through (-3, 4) and normal to -2x + 7y = -3.
Answer:
7x + 2y = – 13