Engage NY Eureka Math Geometry Module 4 Lesson 12 Answer Key
Eureka Math Geometry Module 4 Lesson 12 Exercise Answer Key
Exercise 1.
Find the midpoint of \(\overline{S T}\) given S(- 2, 8) and T(10, – 4).
Answer:
M (\(\frac{1}{2}\)(-2 + 10), \(\frac{1}{2}\)(8 – 4)) = M(4, 2)
Exercise 2.
Find the point on the directed segment from (- 2, 0) to (5, 8) that divides it in the ratio of 1: 3.
Answer:
A ratio of 1:3 means \(\frac{1}{4}\) of the way from (- 2, 0) to (5, 8).
(- 2 + \(\frac{1}{4}\)(5 – (-2)), 0 + \(\frac{1}{4}\)(8 – 0)) = (-\(\frac{1}{4}\), 2)
Exercise 3.
Given \(\overline{P Q}\) and point R that lies on \(\overline{P Q}\) such that point R lies \(\frac{7}{9}\) of the length of \(\overline{P Q}\) from point P along \(\overline{P Q}\):
a. Sketch the situation described.
Answer:

b. Is point R closer to P or closer to Q, and how do you know?
Answer:
R is closer to Q because it lies more than halfway along the segment from point P.
c. Use the given information to determine the following ratios:
i. PR: PQ
Answer:
PR: PQ = 7: 9
ii. RQ: PQ
Answer:
RQ: PQ = 2: 9
iii. PR: RQ
Answer:
PR: RQ = 7: 2
iv. RQ: PR
Answer:
RQ: PR = 2: 7
d. If the coordinates of point P are (0, 0) and the coordinates of point R are (14, 21), what are the coordinates of point Q?
Answer:
(18, 27)
Exercise 4.
A robot is at position A(40, 50) and is heading toward the point 8(2000, 2000) along a straight line at a constant speed. The robot will reach point B in 10 hours.
a. What is the location of the robot at the end of the third hour?
Answer:
(628, 635); The robot will be located \(\frac{3}{10}\) of the length of \(\overline{A B}\) away from point A along \(\overline{A B}\).
(40 + \(\frac{3}{10}\)(2000 – 40), 50 + \(\frac{3}{10}\)(2000 – 50))
b. What is the location of the robot five minutes before it reaches point B?
Answer:
(1983\(\frac{2}{3}\), 1983\(\frac{3}{4}\)); The robot will be located \(\frac{595}{600}\) of the length of \(\overline{A B}\) away from point A along \(\overline{A B}\).
(40 + \(\frac{595}{600}\)(2000 – 40), 50 + \(\frac{595}{600}\)(2000 – 50))
c. If the robot keeps moving along the straight path at the same constant speed as it passes through point B, what will be Its location at the twelfth hour?
Answer:
(2392, 2390); The robot will be located \(\frac{12}{10}\) of the length of \(\overline{A B}\) away from point A along \(\overline{A B}\).
(40 + \(\frac{12}{10}\)(2000 – 40), 50 + \(\frac{12}{10}\)(2000 – 50))
d. Compare the value of the abscissa (x-coordinate) to the ordinate (y-coordinate) before, at, and after the robot passes point B.
Answer:
Initially, the abscissa was less than the ordinate. As the robot moved toward point B, these values got closer to being equal. At point B they were equal, and, for all points on the path beyond point B, the y-coordinate was less than the x-coordinate.
e. Could you have predicted the relationship that you noticed in part (d) based on the coordinates of points A and B?
Answer:
Yes. If point A was located at the origin, the path that the robot took would have been described by the equation y = x; then at each location the robot occupied, the x- and the y-coordinates would have been equal. Point A actually lies above the origin, making the slope of the line that describes the robot’s actual path less than one. Initially, the y-coordinate of each point (location) is greater than the x-coordinate because the line has a y-intercept greater than zero. The slope of the line is less than 1, so as the robot moves to the right, the “gap” closes because for each unit the robot moves to the right, it moves less than one unit up. When the robot reaches point 8(2000, 2000), the abscissa and the ordinate are equal. Beyond point B the x-coordinate will be greater than the y-coordinate.
Eureka Math Geometry Module 4 Lesson 12 Problem Set Answer Key
Question 1.
Given F(0, 2) and G(2, 6), if point S lies \(\frac{5}{12}\) of the way along \(\overline{F G}\), closer to F than to G, find the coordinates of S. Then verify that this point lies on \(\overline{F G}\).
Answer:

Question 2.
Point C lies \(\frac{5}{6}\) of the way along \(\overline{A B}\), closer to B than to A. If the coordinates of point A are (12, 5) and the coordinates of point C are (9. 5, – 2. 5), what are the coordinates of point B?
Answer:
B(9, – 4)
Question 3.
Find the point on the directed segment from (- 3, – 2) to (4, 8) that divides it into a ratio of 3:2.
Answer:
(\(\frac{6}{5}\), 4)
Question 4.
A robot begins Its journey at the origin, point 0, and travels along a straight line path at a constant rate. Fifteen minutes into its journey the robot is at A(35, 80).
a. If the robot does not change speed or direction, where will it be 3 hours into its journey (call this point B)?
Answer:
(35 × 12, 80 × 12) = (420, 960). Multiply by 12 since there are twelve 15-minute periods in 3 hours.
b. The robot continues past point B for a certain period of time until it has traveled an additional \(\frac{3}{4}\) of the distance it traveled in the first 3 hours and stops.
i. How long did the robot’s entire journey take?
Answer:
3 hours × 1\(\frac{3}{4}\) = 5\(\frac{1}{4}\) hours
ii. What is the robot’s final location?
Answer:
(420 × 1.75,960 × 1.75) = (735, 1680)
iii. What was the distance the robot traveled in the last leg of its journey?
Answer:
\(\sqrt{(735-420)^{2}+(1680-960)^{2}}\) ≈ 785.9
The distance is 785.9 units.
Question 5.
Given \(\overline{L M}\) and point R that lies on \(\overline{L M}\), identify the following ratios given that point R lies \(\frac{a}{b}\) of the way along \(\overline{L M}\), closer to L than to M.
a. LR: LM
Answer:
LR: LM = a: b
b. RM: L
Answer:
RM: LM = (b – a): b
c. RL: RM
Answer:
RL: RM a: (b – a)
Question 6.
Given \(\overline{A B}\) with midpoint M as shown, prove that the point on the directed segment from A to B that divides \(\overline{A B}\) into a ratio of 1: 3 is the midpoint of \(\overline{A M}\).
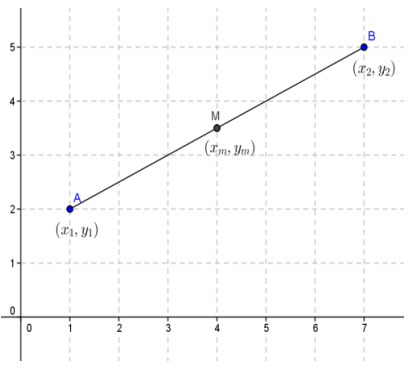
Answer:

Eureka Math Geometry Module 4 Lesson 12 Exit Ticket Answer Key
Question 1.
Given points A(3, -5) and B(19, -1), find the coordinates of point C that sit \(\frac{3}{8}\) of the way along \(\overline{A B}\), closer to A than to B.
Answer:
3 + \(\frac{3}{8}\)(19 – 3), – 5 + (- 1 – (- 5))) = (3 + \(\frac{3}{8}\)(16), – 5 + \(\frac{3}{8}\) (4)
= (3 + 6,-5 + 1.5)
= (9, -3.5)
Question 2.
Given points A(3, -5) and B(19, -1), find the coordinates of point C such that \(\frac{C B}{A C}\) = \(\frac{1}{7}\).
Answer:
(3 + \(\frac{7}{8}\)(19 – 3), – 5 + \(\frac{7}{8}\)(- 1 – (-5))) = (3 + \(\frac{7}{8}\)(16), – 5 + \(\frac{7}{8}\)(4))
= (3 + 14, -5 + 3.5)
= (17, -1.5)