Engage NY Eureka Math Geometry Module 3 Lesson 3 Answer Key
Eureka Math Geometry Module 3 Lesson 3 Exercise Answer Key
Exercise 1.
Rectangles A and B are similar and are drawn to scale. If the area of rectangle A is 88 mm2, what is the area of rectangle B?
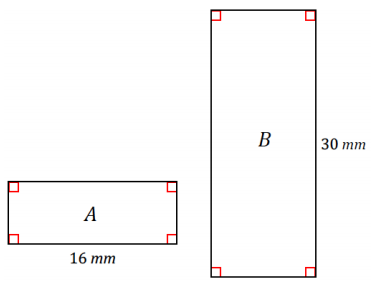
Answer:
Length scale factor: \(\frac{30}{16}=\frac{15}{8}\) = 1.875
Area scale factor: (1.875)2
Area(B) = (1.875)2 × Area(A)
Area(B) = (1.875)2 × 88
Area(B) = 309. 375
The area of rectangle B is 309.375 mm2.
Exercise 2.
Figures E and F are similar and are drawn to scale. If the area of figure E is 120 mm2, what is the area of figure F?
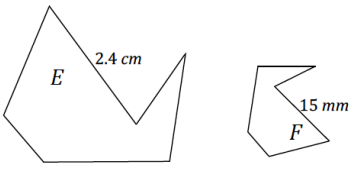
Answer:
2.4 cm = 24 mm
Length scale factor: \(\frac{15}{24}=\frac{5}{8}\) = 0. 625
Area scale factor: (0.625)2
Area(F) = (0.625)2 × Area(E)
Area(F) = (0.625)2 × 120
Area(F) = 46.875
The area of figure F is 46.875 mm2.
THE SCALING PRINCIPLE FOR AREA:
Answer:
If similar figures A and B are related by a scale factor of r, then their respective areas are related by a factor of r2.
Eureka Math Geometry Module 3 Lesson 3 Problem Set Answer Key
Question 1.
A rectangle has an area of 18. Fill in the table below by answering the questions that follow. Part of the first row has been completed for you.
Answer:
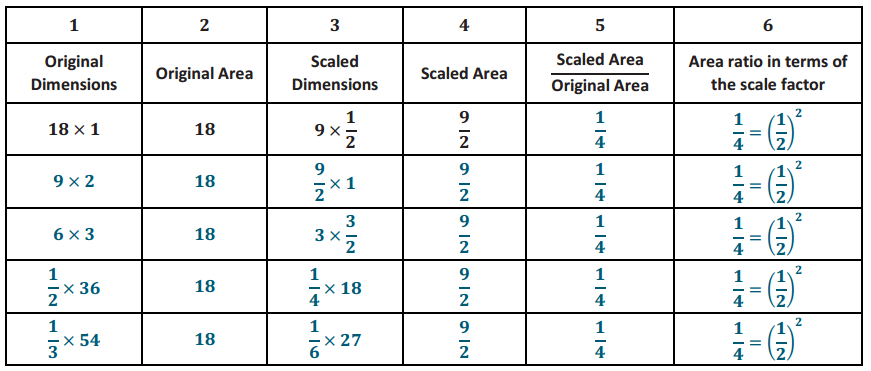
a. List five unique sets of dimensions of your choice for a rectangle with an area of 18, and enter them in column 1.
Answer:
b. If the given rectangle is dilated from a vertex with a scale factor of \(\frac{1}{2}\) what are the dimensions of the images of each of your rectangles? Enter the scaled dimensions in column 3.
Answer:
c. What are the areas of the images of your rectangles? Enter the areas in column 4.
Answer:
d. How do the areas of the images of your rectangles compare to the area of the original rectangle? Write the value of each ratio in simplest form in column 5.
Answer:
e. Write the values of the ratios of area entered in column 5 in terms of the scale factor \(\frac{1}{2}\). Enter these values in column 6.
Answer:
f. If the areas of two unique rectangles are the same, x, and both figures are dilated by the same scale factor r, what can we conclude about the areas of the dilated Images?
Answer:
The areas of the dilated images would both be r2x and thus equal.
Question 2.
Find the ratio of the areas of each pair of similar figures. The lengths of corresponding line segments are shown.
a.
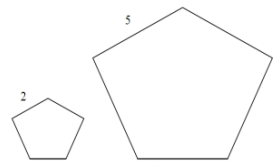
Answer:
The scale factor that takes the smaller pentagon to the larger pentagon is \(\frac{5}{2}\). The area of the larger pentagon is equal to the area of the smaller pentagon times \(\left(\frac{5}{2}\right)^{2}=\frac{25}{4}\). Therefore, the ratio of the area of the smaller pentagon to the larger pentagon is 4:25.
b.
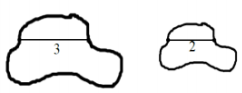
Answer:
The scale factor that takes the larger region to the smaller region is \(\frac{2}{3}\). The area of the smaller region is equal to the area of the larger region times \(\left(\frac{2}{3}\right)^{2}\) or \(\frac{4}{9}\) Therefore, the ratio of the area of the larger region to the smaller region is 9: 4.
c.

Answer:
The scale factor that takes the small star to the large star is \(\frac{7}{4}\). The area of the large star is equal to the area of the small star times \(\left(\frac{7}{4}\right)^{2}\)2 = \(\frac{49}{16}\) Therefore, the ratio of the area of the small star to the area of the large star is 16: 49.
Question 3.
In ∆ ABC, line segment DE connects two sides of the triangle and is parallel to line segment BC. If the area of ∆ ABC is 54 and BC = 3DE, find the area of ∆ ADE.

Answer:
The smaller triangle is similar to the larger triangle with a scale factor of \(\frac{1}{3}\). So, the area of the small triangle is \(\left(\frac{1}{3}\right)^{2}\) = \(\frac{1}{9}\) the area of the large triangle.
Area(ADE) = \(\frac{1}{9}\)(54)
Area(ADE) = 6
The area of ∆ ADE is 6 square units.
Question 4.
The small star has an area of 5. The large star is obtained from the small star by stretching by a factor of 2 in the horizontal direction and by a factor of 3 in the vertical direction. Find the area of the large star.

Answer:
The area of a figure that is scaled in perpendicular directions is equal to the area of the original figure times the product of the scale factors for each direction. The large star therefore has an area equal to the original star times the product 3 · 2.
Area = 5 · 3 · 2
Area = 30
The area of the large star is 30 square units.
Question 5.
A piece of carpet has an area of 50 yd2. How many square inches will this be on a scale drawing that has 1 in. represent 1 yd.?
Answer:
One square yard will be represented by one square inch. So, 50 square yards will be represented by 50 square inches.
Question 6.
An isosceles trapezoid has base lengths of 12 in. and 18 in. If the area of the larger shaded triangle is 72 in2, find the area of the smaller shaded triangle.
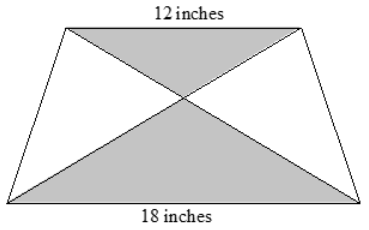
Answer:
The triangles must be similar by AA criterion, so the smaller triangle is the result of a similarity transformation of the larger triangle including a dilation with a scale factor of \(\frac{12}{18}=\frac{2}{3}\). By the scaling principle for area, the area of the smaller triangle must be equal to the area of the larger triangle times the square of the scale factor used:
Area(small triangle) = \(\left(\frac{2}{3}\right)^{2}\). Area(large triangle)
Area(small triangle) = \(\frac{4}{9}\)(72)
Area(small triangle) = 32
The area of the smaller triangle with base 12 in. is 32 in2.
Question 7.
Triangle ABO has a line segment A’B’ connecting two of its sides so that \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\) II \(\overline{A B}\). The lengths of certain segments are given. Find the ratio of the area of triangle OA’B’ to the area of the quadrilateral ABB’A’.
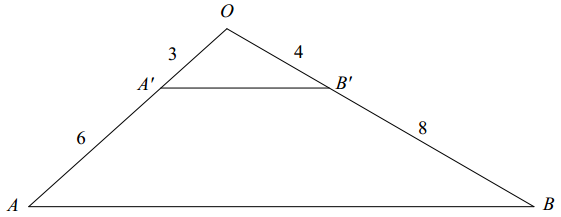
Answer:
∆ OA’B’ ~ ∆ OAB. The area of ∆OA’B’ is \(\frac{1}{9}\) of the area of the area of ∆ OAB because \(\left(\frac{3}{3+6}\right)^{2}\) = \(\left(\frac{1}{3}\right)^{2}\) = \(\frac{1}{9}\) So, the area of the quadrilateral is \(\frac{8}{9}\) of the area of ∆ OAB. The ratio of the area of A OA’B’ to the area of the quadrilateral ABB’A’ is \(\frac{1}{9}\) : \(\frac{8}{9}\), or 1 : 8.
Question 8.
A square region S is scaled parallel to one side by a scale factor of r, r ≠ 0, and is scaled in a perpendicular direction by a scale factor of one-third of r to yield its image S’. What is the ratio of the area of S to the area of S’?
Answer:
Let the sides of square S be s. Therefore, the resulting scaled image would have lengths rs and \(\frac{1}{3}\)rs. Then the area of square S would be s2, and the area of S’ would be \(\frac{1}{3}\) rs(rs) or \(\frac{1}{3}\)(rs)2 or \(\frac{1}{3}\)r2s2.
The ratio of areas of S to S’ is then s2 : \(\frac{1}{3}\)r2 s2 or 1: \(\frac{1}{3}\) r2 or 3: r2.
Question 9.
Figure T’ is the image of figure T that has been scaled horizontally by a scale factor of \(\frac{1}{3}\). and vertically by a scale factor of \(\frac{1}{3}\). If the area of T’ is 24 square units, what is the area of figure T?
Answer:
Area(T’) = \(\frac{1}{3}\) · 4 · Area(T)
24 = \(\frac{4}{3}\) Area(T)
\(\frac{3}{4}\) · 24 = Area(T)
18 = Area(T)
The area of T is 18 square units.
Question 10.
What is the effect on the area of a rectangle if …
a. Its height is doubled and base left unchanged?
Answer:
The area would double.
b. Its base and height are both doubled?
Answer:
The area would quadruple.
c. Its base is doubled and height cut in half?
Answer:
The area would remain unchanged.
Eureka Math Geometry Module 3 Lesson 3 Exit Ticket Answer Key
In the following figure, \(\overline{A E}\) and \(\overline{B D}\) are segments.

a. ∆ ABC and ∆ CDE are similar. How do we know this?
Answer:
The triangles are similar by the AA criterion.
b. What is the scale factor of the similarity transformation that takes ∆ ABC to ∆ CDE?
Answer:
r = \(\frac{4}{11}\)
c. What is the value of the ratio of the area of ∆ ABC to the area of ∆ CDE? Explain how you know.
Answer:
r2 = \(\left(\frac{4}{11}\right)^{2}\) , or \(\frac{16}{121}\) by the scaling principle for triangles.
d. If the area of ∆ ABC is 30 cm2, what is the approximate area of ∆ CDE?
Area(∆ CDE) = \(\frac{16}{121}\) × 30 cm2 4 cm2
Eureka Math Geometry Module 3 Lesson 3 Exploratory Challenge Answer Key
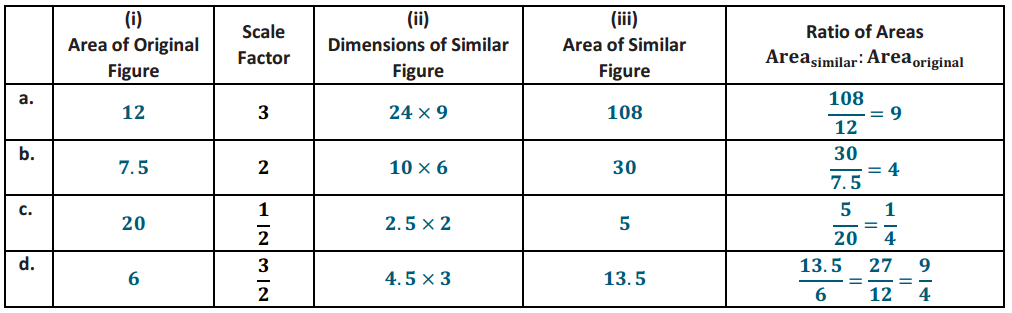
Complete parts (i)-(iii) of the table for each of the figures in questions (a)-(d): (i) Determine the area of the figure (pre image), (ii) determine the scaled dimensions of the figure based on the provided scale factor, and (iii) determine the area of the dilated figure. Then, answer the question that follows.
In the final column of the table, find the value of the ratio of the area of the similar figure to the area of the original figure.
Answer:
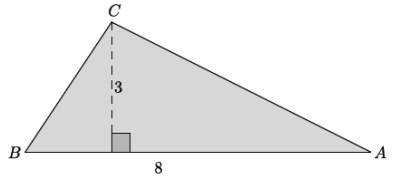
a.
Answer:
i. \(\frac{1}{2}\)(8)(3) = 12
ii. The base of the simllar, triangle is 8(3) or 24, and the height of the shelar triangle is 3(3) or 9.
iii. \(\frac{1}{2}\)(24)(9) = 108
b.
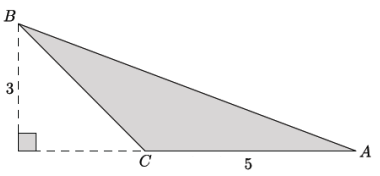
Answer:
i. \(\frac{1}{2}\)(5)(3) – 7.5
ii. The base of the similar triangle is 5(2) or 10, and the height of the similar triangle Is 3(2) or 6.
iii. \(\frac{1}{2}\)(10)(6) = 3o
c.
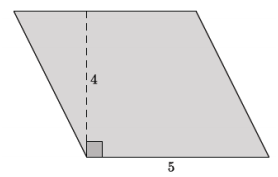
Answer:
i. (5)(4) = 20
ii. The base of the similar parallelogram is 5\(\left(\frac{1}{2}\right)\) or 2.5, and the height of the similar parallelogram is 4\(\) or 2.
iii. 2.5(2) = 5
d.
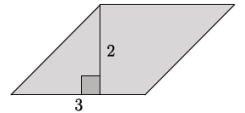
Answer:
i. (3)(2) = 6
ii. The base of the similar parallelogram is 3\(\left(\frac{3}{2}\right)\) or 4.5, and the height of the similar parallelogram is 2\(\left(\frac{2}{3}\right)\) or 3.
iii. 4.5(3) = 13.5
e. Make a conjecture about the relationship between the areas of the original figure and the similar figure with respect to the scale factor between the figures.
Answer:
It seems as though the value of the ratio of the area of the similar figure to the area of the original figure is the square of the scale factor of dilation.
THE SCALING PRINCIPLE FOR TRIANGLES:
Answer:
If similar triangles S and T are related by a scale factor of r, then the respective areas are related by a factor of r2.
THE SCALING PRINCIPLE FOR POLYGONS:
Answer:
If similar polygons P and Q are related by a scale factor of r, then their respective areas are related by a factor of r2.