Engage NY Eureka Math Geometry Module 3 Lesson 2 Answer Key
Eureka Math Geometry Module 3 Lesson 2 Exploratory Challenge/Exercise Answer Key
Exercise 1.
Two congruent triangles are shown below.
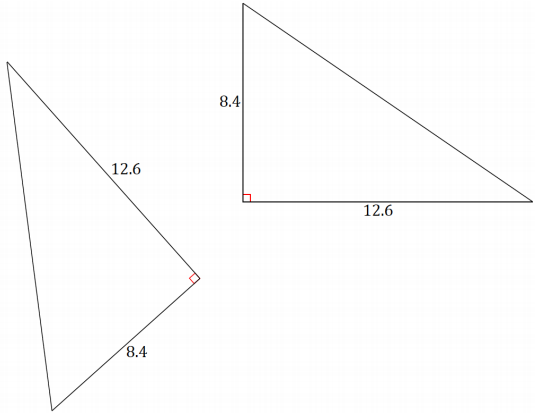
a. Calculate the area of each triangle.
Answer:
\(\frac{1}{2}\)(12.6)(8.4) = 52.92
b. Circle the transformations that, if applied to the first triangle, would always result in a new triangle with the same area:
Answer:

c. Explain your answer to part (b).
Answer:
Two congruent figures have equal area. If two figures are congruent, it means that there exists a transformation that maps one figure onto the other completely. For this reason, it makes sense that they would have equal area because the figures would cover the exact same region.
Exercise 2.
a. Calculate the area of the shaded figure below.
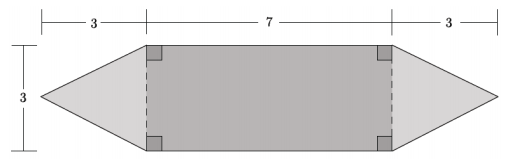
Answer:
2\(\left(\frac{1}{2}\right)\)(3)(3) = 9
7(3) = 21
Area = 9 + 21 = 30
The area of the shaded figures is 30.
b. Explain how you determined the area of the figure.
Answer:
First, I realized that the two shapes at the ends of the figure were triangles with a base of 3 and a height of 3 and that the shape in the middle was a rectangle with dimensions 3 × 7. To find the area of the shaded figure, I found the sum of all three shapes.
Exercise 3.
Two triangles ∆ ABC and ∆ DEF are shown below. The two triangles overlap forming ∆ DGC.
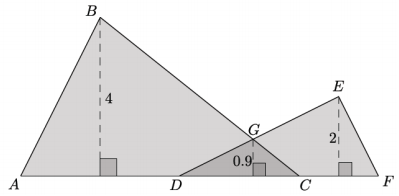
a. The base of figure ABGEF is composed of segments of the following lengths: AD = 4, DC = 3, and CF = 2. Calculate the area of the figure ABGEF.
Answer:
The area of ∆ ABC: \(\frac{1}{2}\)(4)(7) = 14
The area of ∆ DEF: \(\frac{1}{2}\)(2)(5) = 5
The area of ∆ DGC: \(\frac{1}{2}\)(0.9)(3) = 1.35
The area of figure ABGEF is 14 + 5 – 1.35, or 17.65.
b. Explain how you determined the area of the figure.
Answer:
Since the area of ∆ DGC is counted twice, It needs to be subtracted from the sum of the overlapping triangles.
Exercise 4.
A rectangle with dimensions 21. 6 × 12 has a right triangle with a base 9. 6 and a height of 7. 2 cut out of the rectangle.
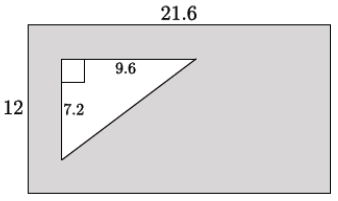
a. Find the area of the shaded region.
Answer:
The area of the rectangle: (12)(21.6) = 259.2
The area of the triangle: \(\frac{1}{2}\)(7. 2)(9. 6) = 34.56
The area of the shaded region is 259.2 – 34.56, or 224.64.
b. Explain how you determined the area of the shaded region.
Answer:
I subtracted the area of the triangle from the area of the rectangle to determine the shaded region.
Eureka Math Geometry Module 3 Lesson 2 Problem Set Answer Key
Question 1.
Two squares with side length 5 meet at a vertex and together with segment AB form a triangle with base 6 as shown. Find the area of the shaded region.
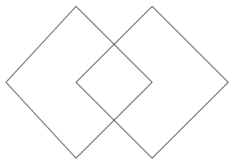
Answer:
The altitude of the isosceles triangle splits it into two right triangles, each having a base of 3 units in length and hypotenuse of 5 units in length. By the Pythagorean theorem, the height of the triangles must be 4 units in length. The area of the isosceles triangle is 12 square units. Since the squares and the triangle share sides only, the sum of their areas is the area of the total figure. The areas of the square regions are each 25 square units, making the total area of the shaded region 62 square units.
Question 2.
If two 2 × 2 square regions S1 and S2 meet at midpoints of sides as shown, find the area of the square region, S1 ∪ S2.
Answer:
The area of S1 ∩ S2 = 1 because it is a 1 × 1 square region.
Area(S1) = Area(S2) = 4
By Property 3, the area of S1 ∪ S2 = 4 + 4 – 1 = 7.
Question 3.
The figure shown is composed of a semicircle and a non-overlapping equilateral triangle, and contains a hole that is also composed of a semicircle and a non-overlapping equilateral triangle. If the radius of the larger semicircle is 8, and the radius of the smaller semicircle is \(\frac{1}{3}\) that of the larger semicircle, find the area of the figure.
Answer:
The area of the large semicircle: Area = \(\frac{1}{2}\) π · 82 = 32π
The area of the smaller semicircle: Area = \(\frac{1}{2}\) π \(\left(\frac{8}{3}\right)^{2}\) = \(\frac{32}{9}\) π
The area of the large equilateral triangle: Area = \(\frac{1}{2}\) · 16 ·
The area of the smaller equilateral triangle: Area = \(\frac{1}{2} \cdot \frac{16}{3} \cdot \frac{8}{3} \sqrt{3}=\frac{64}{9} \sqrt{3}\)
Total Area:
Total area = 32π – \(\frac{32}{9}\)π + 64√3 – \(\frac{64}{9}\)√3
Total area = \(\frac{256}{9} \pi+\frac{512}{9} \sqrt{3}\) ≅ 188
The area of the figure is approximately 188.
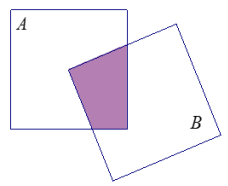
Question 4.
Two square regions A and B each have Area(8). One vertex of square B is the center point of square A. Can you find the area of A ∪ B and A ∩ B without any further information? What are the possible areas?
Answer:
Rotating the shaded area about the center point of square A by a quarter turn three times gives four congruent non-overlapping regions. Each region must have area one-fourth the area of the square. So, the shaded region has Area(2).
Area(A ∪ B) = 8 + 8 – 2 = 14
Area(A ∩ B) = 2
Question 5.
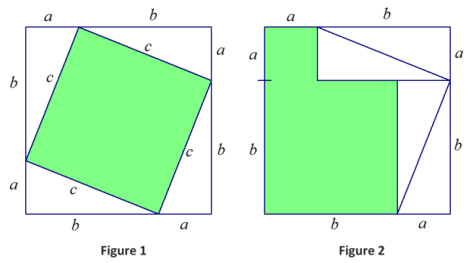
Four congruent right triangles with leg lengths a and b and hypotenuse length c are used to enclose the green region in Figure 1 with a square and then are rearranged inside the square leaving the green region in Figure 2.

a. Use Property 4 to explain why the green region in Figure 1 has the same area as the green region in Figure 2.
Answer:
The white polygonal regions in each figure have the same area, so the green region (difference of the big square and the four triangles) has the same area in each figure.
b. Show that the green region in Figure 1 is a square, and compute its area.
Answer:
Each vertex of the green region is adjacent to the two acute angles in the congruent right triangles whose sum is 90°. The adjacent angles also lie along a line (segment), so their sum must be 180°. By addition, it follows that each vertex of the green region in Figure 1 has a degree measure of 90°. This shows that the green region is at least a rectangle.
The green region was given as having side lengths of C, so together with having four right angles, the green region must be a square.
c. Show that the green region in Figure 2 is the union of two non-overlapping squares, and compute its area.
Answer:
The congruent right triangles are rearranged such that their acute angles are adjacent, forming a right angle. The angles are adjacent to an angle at a vertex of an a × a green region, and since the angles are all adjacent along a line (segment), the angle in the green region must then be 90°. If the green region has four sides of length a, and one angle is 90°, the remaining angles must also be 90°, and the region a square.
A similar argument shows that the green b × b region is also a square. Therefore, the green region in Figure 2 is the union of two non-overlapping squares. The area of the green region is then a2 + b2.
d. How does this prove the Pythagorean theorem?
Answer:
Because we showed the green regions in Figures 1 and 2 to be equal in area, the sum of the areas in Figure 2 being a2 + b2, therefore, must be equal to the area of the green square region in Figure 1, c2. The lengths a, b, and c were given as the two legs and hypotenuse of a right triangle, respectively, so the above line of questions shows that the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse.
Eureka Math Geometry Module 3 Lesson 2 Exit Ticket Answer Key
Question 1.
Wooden pieces in the following shapes and sizes are nailed together to create a sign in the shape of an arrow. The pieces are nailed together so that the rectangular piece overlaps with the triangular piece by 4 in. What is the area of the region in the shape of the arrow?

Answer:
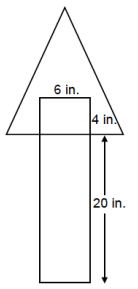
Area(Arrow) = Area(Rectangle) + Area(Triangle) – Area(Overlap)
Area(Arrow) = 144 + 104 – 24
Area(Arrow) = 224
The area of the region in the shape of the arrow is 224 in2.
Question 2.
A quadrilateral Q is the union of two triangles T1 and T2 that meet along a common side as shown in the diagram. Explain why Area(Q) = Area(T1) + Area(Tz).
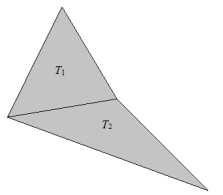
Answer:
Q = T1 ∪ T2, so Area(Q) = Area(T1) + Area(T2) – Area(T1 ∩ T2)
Since T1 ∩ T2 is a line segment, the area of T1 ∩ T2 is 0.
Area(T1) + Area(T2) – Area(T1 ∩ T2) = Area(T1) + Area(T2) – 0
Area(T1) + Area(T2) – Area(T1 ∩ T2) = Area(T1) + Area(T2)