Engage NY Eureka Math Geometry Module 2 Lesson 9 Answer Key
Eureka Math Geometry Module 2 Lesson 9 Exploratory Challenge/Exercise Answer Key
Exercise 1.
How do dilations map triangles? students make
a. Make a conjecture.
Answer:
A dilation maps a triangle to a triangle with the same angles, and all of the sides of the image triangle are proportional to the sides of the original triangle.
b. Verify your conjecture by experimenting with diagrams and directly measuring angles and lengths of segments.
Answer:
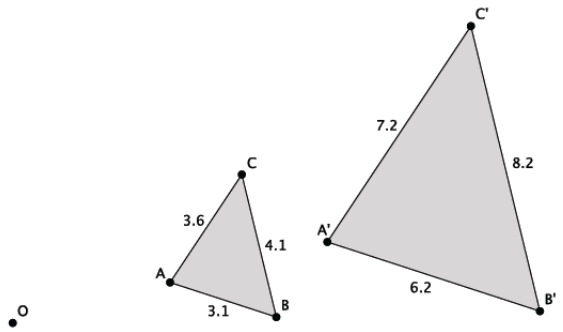
The value of the ratios of the lengths of the dilated triangle to the original triangle is equal to the scale factor. The angles map to angles of equal measure; all of the angles in the original triangle are dilated to angles equal in measure to the corresponding angles in the dilated triangle.
Exercise 2.
How do dilations map rectangles?
a. Make a conjecture.
Answer:
A dilation maps a rectangle to a rectangle so that the ratio of length to width is the same.
b. Verify your conjecture by experimenting with diagrams and directly measuring angles and lengths of segments.
Answer:
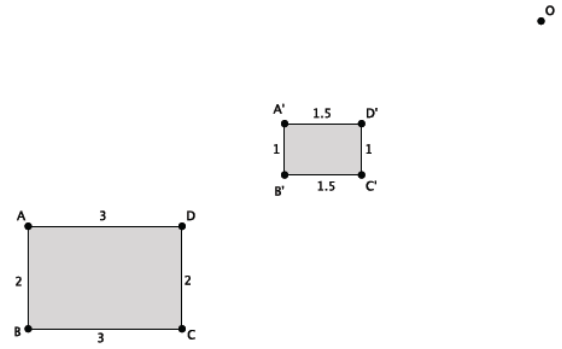
The original rectangle has a length to width ratio of 3: 2. The dilated rectangle has a length to width ratio of 1.5: 1. The values of the ratios are equal. Since angles map to angles of equal measure, all of the right angles in the original rectangle are dilated to right angles.
Exercise 3.
How do dilations map squares?
a. Make a conjecture.
Answer:
A dilation maps a square with side length L to a square with side length rL where r is the scale factor of dilation. Since each segment of length L is mapped to a segment of length rL and each right angle is mapped to a right angle, then the dilation maps a square with side length L to a square with side length rL.
b. Verify your conjecture by experimenting with diagrams and directly measuring angles and lengths of segments.
Answer:
Sample student drawing:
The side length of the original square is 2 units. The side length of the dilated square is 6 units. The side length of the dilated square is equal to the length of the original square multiplied by the scale factor. Since angles map to angles of equal measure, all of the right angles in the original square are dilated to right angles.
Exercise 4.
How do dilations map regular polygons?
a. Make a conjecture.
Answer:
A dilation maps a regular polygon with side length L to a regular polygon with side length rL where r is the scale factor of dilation. Since each segment of length L is mapped to a segment of length rL and each angle is mapped to an angle that is equal in measure, then the dilation maps a regular polygon with side length L to a regular polygon with side length rL.
b. Verify your conjecture by experimenting with diagrams and directly measuring angles and lengths of segments.
Answer:
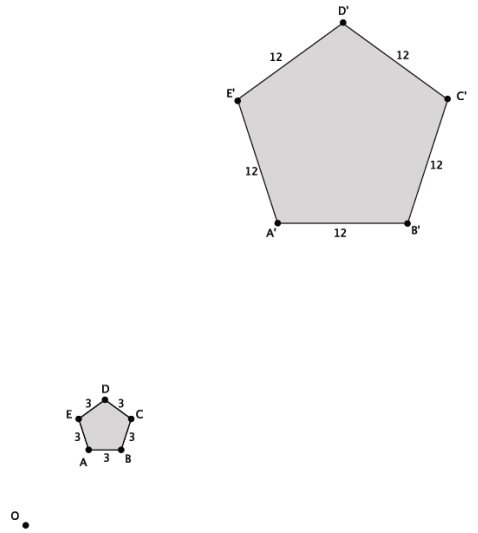
The side length of the original regular polygon is 3 units. The side length of the dilated regular polygon is 12 units. The side length of the dilated regular polygon is equal to the length of the original regular polygon multiplied by the scale factor. Since angles map to angles of equal measure, all of the angles in the original regular polygon are dilated to angles of each measure.
Exercise 5.
Recall what you learned about parallel lines cut by a transversal, specifically about the angles that are formed.
Answer:
When parallel lines are cut by a transversal, then corresponding angles are equal in measure, alternate interior angles are equal in measure, and alternate exterior angles are equal in measure.
Exercise 6.
A dilation from center O by scale factor r maps ∠BAC to ∠B’A’C’. Show that m∠BAC = m∠B’A’C’.
Answer:
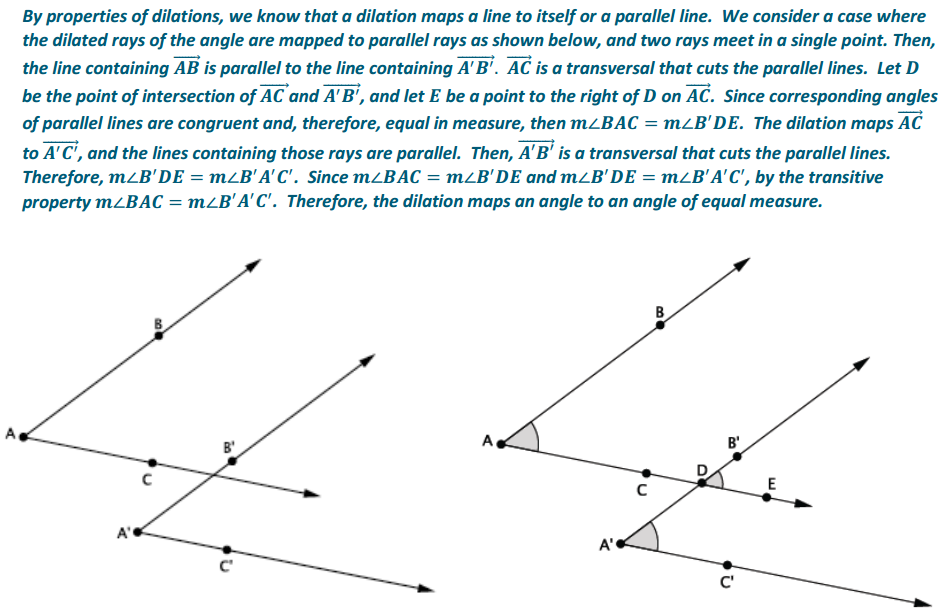
Discussion:
The dilation theorem for angles is as follows:
DILATION THEOREM: A dilation from center O and scale factor r maps an angle to an angle of equal measure.
We have shown this when the angle and its image intersect at a single point, and that point of intersection is not the vertex of the angle.
Answer:
→ So far, we have seen the case when the angles intersect at a point. What are other possible cases that we need to consider?
Provide time for students to identify the two other cases: (1) The angles do not intersect at a point, and (2) the angles have vertices on the same ray. The teacher may need to give students this information if students cannot develop the cases on their own.
→ We will cover another case where a dilation maps ∠BAC to ∠B’A’C’. When the angle and its dilated image do not have intersecting rays (as shown below), how can we show that the angle and its dilated image are equal in measure?
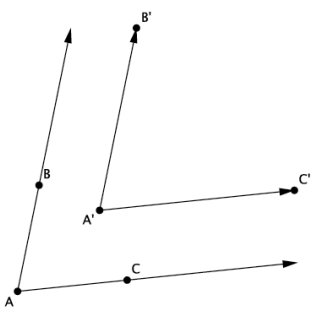
If students do not respond, the teacher may need to give the information in the bullet point below.
You can draw an auxiliary line and use the same reasoning to show that the angle and its ima ge are equal in measure.
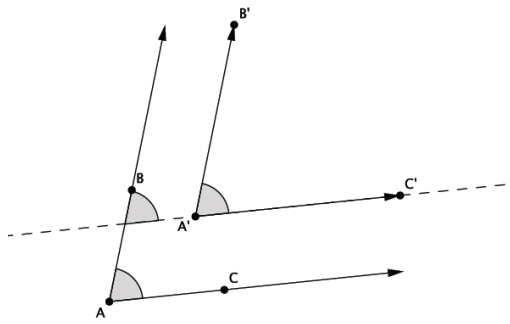
→ Notice now that by drawing the auxiliary line, we have two angles that intersect at a point, much like we had in the Opening Exercise. Therefore, the same reasoning shows that m∠BAC = m∠B’A’C’.
→ The only case left to consider is when the line containing a ray also contains the image of the ray. In this case, ray BC and ray B’C’ lie in the same line.
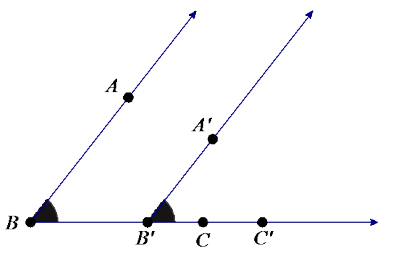
→ Why does m∠ABC = m∠A’B’C’?
They are corresponding angles from parallel lines cut by a transversal.
Eureka Math Geometry Module 2 Lesson 9 Problem Set Answer Key
Question 1.
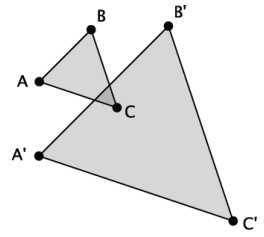
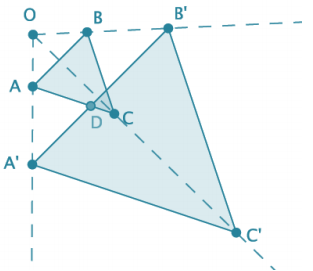
Shown below is ∆ ABC and its image ∆ A’B’C’ after it has been dilated from center O by scale factor r = \(\frac{5}{2}\).
Prove that the dilation maps ∆ ABC to ∆ A’B’C’ so that m∠A = m∠A’, m∠B = m∠B’, and m∠C = m∠C’.
Answer:

Question 2.
Explain the effect of a dilation with scale factor r on the length of the base and height of a triangle. How is the area of the dilated image related to the area of the pre-image?
Answer:
Let P represent the endpoint of altitude \(\overline{A P}\) of ∆ ABC, such that P lies on \(\overleftrightarrow{B C}\). Thus, the base length of the triangle is BC, and the height of the triangle is AP. The area of the given triangle then is \(\frac{1}{2}\)(BC) (AP). By the definition of dilation, B’C’ = r(BC) and A’P’ = r(AP), so the base and height of the dilated image are proportional to the base and height of the original just as the lengths of the sides of the triangle. The area of the dilated triangle then would be \(\frac{1}{2}\)(r(BC) ∙ r(AP)) = r2∙ \(\frac{1}{2}\)(BC)(AP).
The ratio of the area of the dilated image to the area of the pre-image is r2.
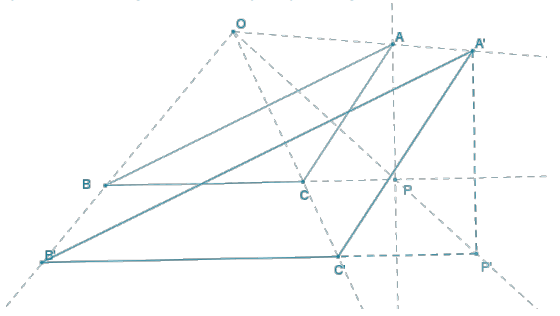
Question 3.
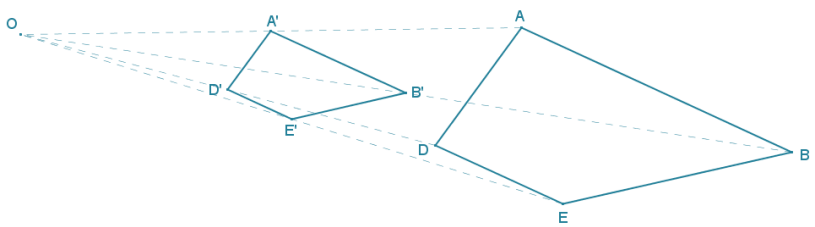
Dilate trapezoid ABED from center O using a scale factor of r = \(\frac{1}{2}\).
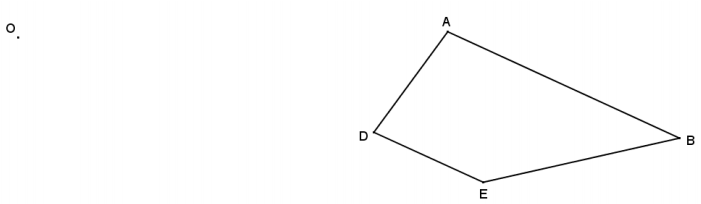
Answer:
A dilation maps a trapezoid to a trapezoid so that the ratio of corresponding sides is the same and corresponding interior angles are the same measure.
Question 4.
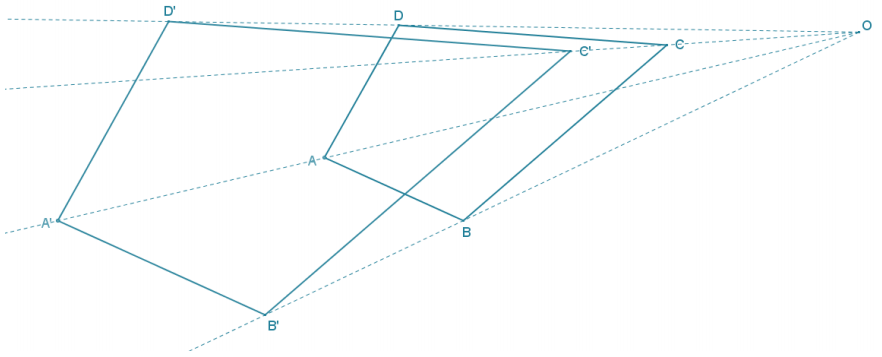
Dilate kite ABCD from center O using a scale factor r = 1\(\frac{1}{2}\).
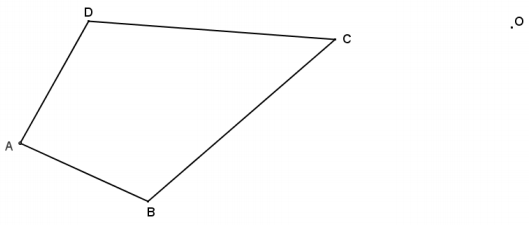
Answer:
A dilation maps a kite to a kite so that the ratio of corresponding sides is the same and corresponding interior angles are the same measure.
Question 5.
Dilate hexagon DEFGHI from center O using a scale factor of r = \(\frac{1}{4}\).
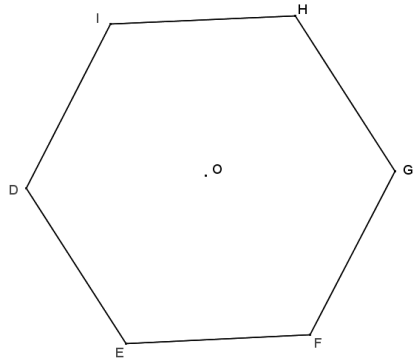
Answer:
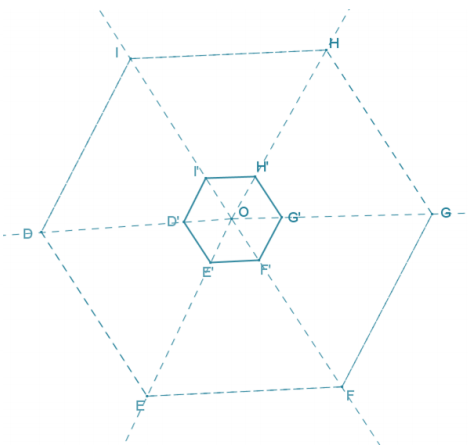
Question 6.
Examine the dilations that you constructed in Problems 2—5, and describe how each image compares to its pre image under the given dilation. Pay particular attention to the sizes of corresponding angles and the lengths of corresponding sides.
Answer:
In each dilation, the angles in the image are the same size as the corresponding angles in the pre-image, as we have shown that dilation preserves angle measure. We also know that the lengths of corresponding sides are in the same ratio as the scale factor.
Eureka Math Geometry Module 2 Lesson 9 Exit Ticket Answer Key
Question 1.
Dilate parallelogram STUV from center O using a scale factor of r = \(\frac{3}{4}\).
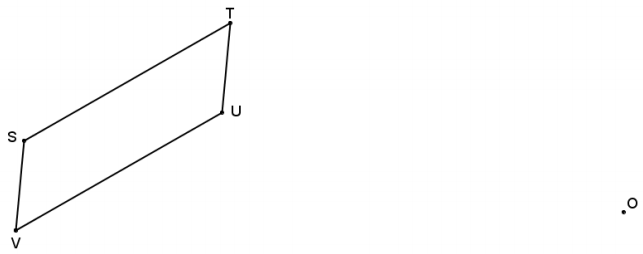
Answer:
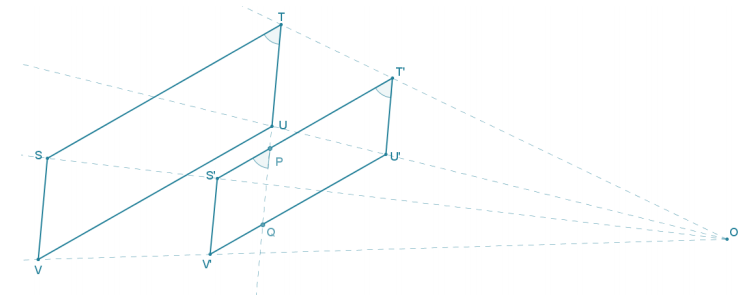
Question 2.
How does m∠T’ compare to mðJ?
Answer:
m∠T’ = m∠T because dilations preserve angle measure.
Question 3.
Using your diagram, prove your claim from Problem 2.
Answer:
