Engage NY Eureka Math Geometry Module 2 Lesson 8 Answer Key
Eureka Math Geometry Module 2 Lesson 8 Example Answer Key
Does a dilation about center O and scale factor r = 1 map \(\overrightarrow{P Q}\) to \(\overrightarrow{P^{\prime} Q^{\prime}}\)? Explain.
Answer:
A scale factor of r = 1 means that the ray and its image are equal. That is, the dilation does not enlarge or shrink the image of the figure but remains unchanged. Therefore, when the scale factor of a dilation is r = 1, then the dilation maps the ray to itself.
Example 2
The line that contains \(\overrightarrow{P Q}\) does not contain point O. Does a dilation D about center O and scale factor r ≠1 map every point of \(\overrightarrow{P Q}\) onto a point of \(\overrightarrow{P^{\prime} Q^{\prime}}\)?
Answer:
→ A restatement of this problem is as follows: If R is a point on \(\overrightarrow{P Q}\), then is D(R) a point on \(\overrightarrow{P^{\prime} Q^{\prime}}\)? Also, if a point S’ lies on the ray \(\overrightarrow{P^{\prime} Q^{\prime}}\), then is there a point S on the ray \(\overrightarrow{P Q}\) such that D(S) = S’?
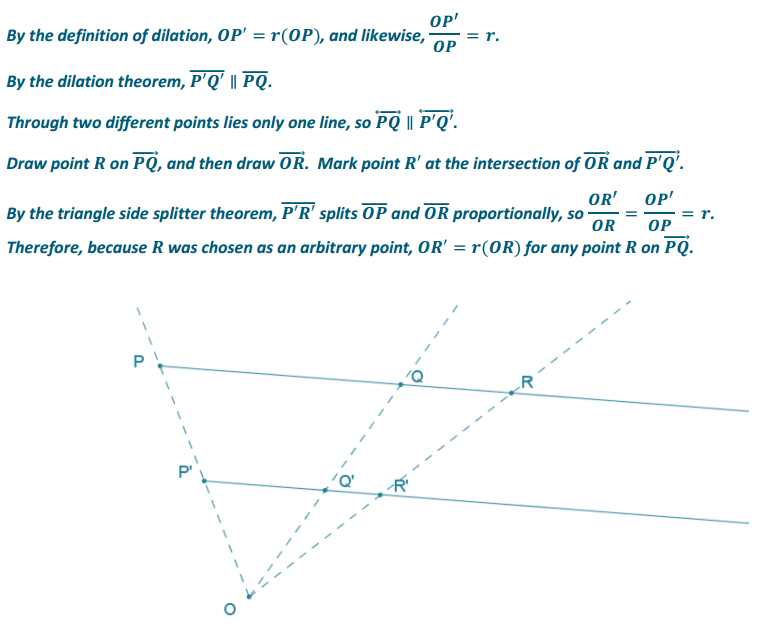
→ Consider the case where the center O is not in the line that contains \(\overrightarrow{P Q}\), and the scale factor is r ≠1. Then, points O, P, and Q form ∆ OPQ.
Draw the following figure on the board.
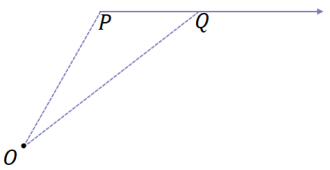
→ We examine the case with a scale factor r > 1; the proof for 0 < r < 1 is similar.
→ Under a dilation about center O and r > 1, P goes to P, and Q goes to Q’; OP’ = r ∙ OP and QQ’ = r ∙ QQ.
What conclusion can we draw from these lengths?
→ Summarize the proof and result to a partner.
Draw the following figure on the board.
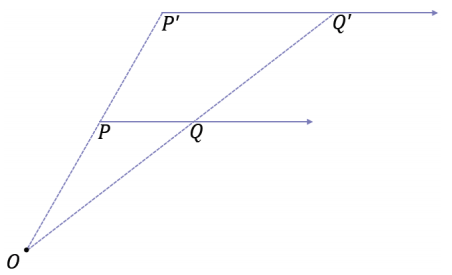
We can rewrite each length relationship as \(\frac{O P^{\prime}}{O P}=\frac{O Q^{\prime}}{O Q}\) r.
→ By the triangle side splitter theorem, what else can we now conclude?
The segment PQ splits ∆ OP’Q’ proportionally.
The lines that contain and \(\overrightarrow{P Q}\) are \(\overrightarrow{P^{\prime} Q^{\prime}}\) parallel; 
.
→ By the dilation theorem for segments (Lesson 7), the dilation from O of the segment PQ is the segment P’Q’, that is, D(\(\overline{P Q}\)) = \(\overline{P^{\prime} Q^{\prime}}\) as sets of points. Therefore, we need only consider an arbitrary point R on \(\overrightarrow{P Q}\) that lies outside of \(\overline{P Q}\). For any such point R, what point is contained in the segment PR?
The point Q
→ Let R’ = D(R).
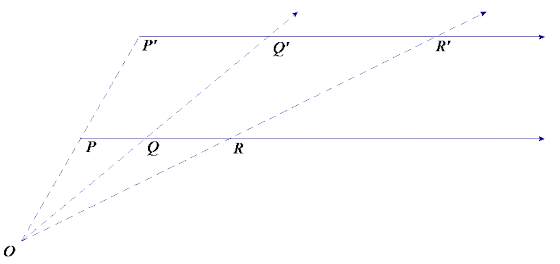
→ By the dilation theorem for segments, the dilation from O of the segment PR is the segment P’R’. Also by the dilation theorem for segments, the point D(Q) = Q’ is a point on segment P’R’. Therefore, \(\overrightarrow{P^{\prime} Q^{\prime}}\) and \(\overrightarrow{P^{\prime} R^{\prime}}\) must be the same ray. In particular, R’ is a point on \(\overrightarrow{P^{\prime} Q^{\prime}}\), which was what we needed to show.
To show that for every point S’ on \(\overrightarrow{P^{\prime} Q^{\prime}}\) there is a point S on \(\overrightarrow{P Q}\) such that D(S) = S’, consider the dilation from center O with scale factor \(\frac{1}{r}\) (the inverse of the dilation D). This dilation maps S’ to a point S on \(\overrightarrow{P R}\) by the same reasoning as above. Then, D(S) = S’.
→ We conclude that the points of \(\overrightarrow{P Q}\) are mapped onto the points of \(\overrightarrow{P^{\prime} Q^{\prime}}\) and, more generally, that dilations map rays to rays.
Example 3
The line that contains \(\overrightarrow{P Q}\) contains point O. Does a dilation about center O and scale factor r map \(\overrightarrow{P Q}\) to \(\overrightarrow{P^{\prime} Q^{\prime}}\)?
Answer:
→ Consider the case where the center O belongs to the line that contains \(\overrightarrow{P^{\prime} Q^{\prime}}\).
a. Examine the case where the endpoint P of \(\overrightarrow{P^{\prime} Q^{\prime}}\) coincides with the center O of the dilation.
Answer:
→ If the endpoint P of \(\overrightarrow{P^{\prime} Q^{\prime}}\) coincides with the center O, what can we say about \(\overrightarrow{P^{\prime} Q^{\prime}}\) and \(\overrightarrow{O^{\prime} Q^{\prime}}\)?
Ask students to draw what this looks like, and draw the following on the board after giving them a head start.
All the points on \(\overrightarrow{O^{\prime} Q^{\prime}}\) also belong to \(\overrightarrow{O Q} ; \overrightarrow{P Q}=\overrightarrow{O Q}\)
→ By definition, a dilation always sends its center to itself. What are the implications for the dilation of O and P?
Since a dilation always sends its center to itself, then O = P = O’ = P’.
→ Let X be a point on \(\overrightarrow{O Q}\) so that X ≠O. What happens to X under a dilation about O with scale factor r?
The dilation sends X to X’ on \(\overrightarrow{O X}\), and OX’ = r ∙ OX.
Ask students to draw what the position of X and X’ might look like if r > 1 or r < 1. Points may move farther away (r> 1) or move closer to the center (r < 1). They do not draw this for every case; rather, it is a reminder up front.
→ Since O, X, and Q are collinear, then O, X’, and Q are also collinear; X’ is on the ray OX, which coincides with \(\overrightarrow{O Q}\) by definition of dilation.
→ Therefore, a dilation of \(\overrightarrow{O Q}\) is \(\overrightarrow{P Q}\) (or when the endpoint of P of \(\overrightarrow{P Q}\) coincides with the center O) about center O and scale factor r maps \(\overrightarrow{O^{\prime} Q^{\prime}}\) to \(\overrightarrow{P^{\prime} Q^{\prime}}\). We have answered the bigger question that a dilation maps a ray to a ray.
b. Examine the case where the endpoint P of \(\overrightarrow{P Q}\) is between O and Q on the line containing O, P, and Q.
Answer:
→ We already know from the previous case that the dilation of the ray \(\overrightarrow{O Q}\) maps onto itself. All we need to show
is that any point on the ray that is farther away from the center than P maps to a point that is farther away from the center than P’.
→ Let X be a point on \(\overrightarrow{P Q}\) so that X ≠P. What can be concluded about the relative lengths of \(\overline{O P}\) and \(\overline{O X}\)?
Ask students to draw what this looks like, and draw the following on the board after giving them a head start. The following is one possibility.
OP < OX
→ Describe how the lengths OP’ and OX’ compare once a dilation about center O and scale factor r sends P to P’ and X to X’.
OP’ = r ∙ OP and OX’ = r ∙ OX
Multiplying both sides of OP < OX by r > O gives r ∙ OP < r ∙ OX, so OP’ < OX’.
Ask students to draw what this might look like if r > 1, and draw the following on the board after giving them a head start.
→ Therefore, we have shown that any point on the ray \(\overrightarrow{P Q}\) that is farther away from the center than P maps to a point that is farther away from the center than P’. In this case, we still see that a dilation maps a ray to a ray.
c. Examine the remaining case where the center O of the dilation and point Q are on the same side of P on the line containing O, P, and Q.
Answer:
→ Now consider the relative position of O and Q on We use an additional point R as a reference point so the O is between P and R.
Draw the following on the board; these are all the ways that O and Q are on the same side of P.
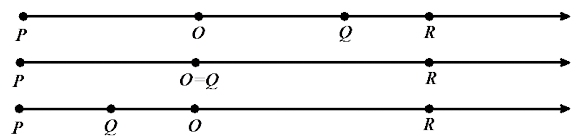
→ By case (a), we know that a dilation with center O maps \(\overrightarrow{O R}\) to itself.
→ Also, by our work in Lesson 7 on how dilations map segments to segments, we know that \(\overline{P O}\) is taken to where \(\overline{P^{\prime} O}\) lies on \(\overrightarrow{O P}\).
→ The union of the \(\overline{P^{\prime} O}\) and \(\overrightarrow{O R}\) is \(\overrightarrow{P^{\prime} R}\). So, the dilation maps \(\overrightarrow{P Q}\) to \(\overrightarrow{P^{\prime} R}\).
→ Since Q’ is a point on \(\overrightarrow{P^{\prime} R}\) and Q’ ≠P’, we see \(\overrightarrow{P^{\prime} R}=\overrightarrow{P^{\prime} Q^{\prime}}\). Therefore, in this case, we still see that \(\overrightarrow{P Q}\) maps to \(\overrightarrow{P^{\prime} Q^{\prime}}\) under a dilation.
Example 4.
Does a dilation about a center O and scale factor r map a circle of radius R onto another circle?
a. Examine the case where the center of the dilation coincides with the center of the circle.
Answer:
→ We first do the case where the center of the dilation is also the center of the circle. Let C be a circle with center O and radius R.
Draw the following figure on the board.
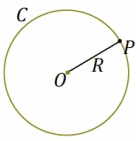
→ If the center of the dilation is also O, then every point P on the circle is sent to a point P’ on \(\overrightarrow{O P}\) so that OP’ = r ∙ OP = rR; that is, the point goes to the point P’ on the circle C’ with center O and radius rR.
→ We also need to show that every point on C’ is the image of a point from C: For every point P’ on circle C’, put a coordinate system on 
such that \(\overrightarrow{O P}\) corresponds to the nonnegative real numbers with zero corresponding to point O (by the ruler axiom). Then, there exists a point P on \(\overrightarrow{O P^{\prime}}\) such that OP = R; that is, P is a point on the circle C that is mapped to P’ by the dilation.
Draw the following figure on the board.
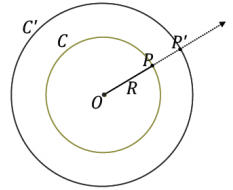
→ Effectively, a dilation moves every point on a circle toward or away from the center the same amount, so the dilated image is still a circle. Thus, the dilation maps the circle C to the circle C’.
→ Circles that share the same center are called concentric circles.
b. Examine the case where the center of the dilation is not the center of the circle; we call this the general case.
Answer:
→ The proof of the general case works no matter where the center of the dilation is. We can actually use this proof for case (a), when the center of the circle coincides with the center of dilation.
→ Let C be a circle with center O and radius R. Consider a dilation with center D and scale factor r that maps O to O’. We will show that the dilation maps the circle C to the circle C’ with center O’ and radius rR.
Draw the following figure on the board.
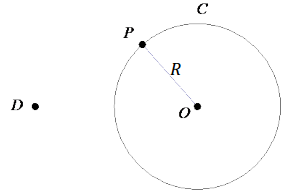
→ If P is a point on circle C and the dilation maps P to P’, the dilation theorem implies that O’P’ = r OP = rR. So, P’ is on circle C’.
→ The diagram below shows how the dilation maps points P, Q, R, S, and T of circle C. Ask students to find point W on circle C that is mapped to point W’ on circle C’.
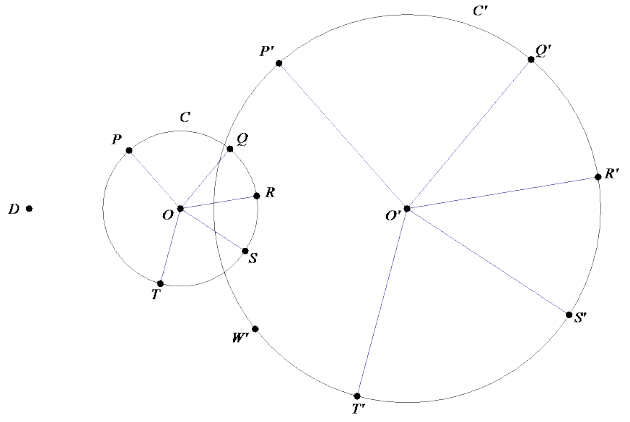
Eureka Math Geometry Module 2 Lesson 9 Opening Exercise Answer Key
a. Is a dilated ray still a ray? If the ray is transformed under a dilation, explain how.
Answer:
Accept any reasonable answer. The goal of this line of questioning is for students to recognize that a segment dilates to a segment that is r times the length of the original.
b. Dilate the ray \(\overrightarrow{P Q}\) by a scale factor of 2 from center O.
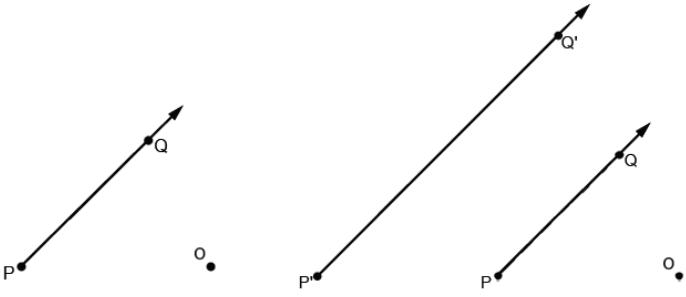
i. Is the figure \(\overrightarrow{P^{\prime} Q^{\prime}}\) a ray?
Answer:
Yes. The dilation of ray PQ produces a ray P’Q’.
ii. How, if at all, has the segment PQ been transformed?
Answer:
The segment P’Q’ in ray P’Q’ is twice the length of the segment PQ in ray PQ. The segment has increased in length according to the scale factor of dilation.
iii. Will a ray always be mapped to a ray? Explain how you know.
Answer:
Students will most likely say that a ray always maps to a ray; they may defend their answers by citing the definition of a dilation and its effect on the center and a given point.
Eureka Math Geometry Module 2 Lesson 8 Problem Set Answer Key
Question 1.
In Lesson 8, Example 2, you proved that a dilation with a scale factor r > 1 maps a ray PQ to a ray P’Q’. Prove the remaining case that a dilation with scale factor 0 < r < 1 maps a ray PQ to a ray P’Q’.
Given the dilation D0, with 0 < r < 1 maps P to P’ and Q to Q’, prove that Do,r maps \(\overrightarrow{P Q}\) to \(\overrightarrow{P^{\prime} Q^{\prime}}\).
Answer:
Question 2.
In the diagram below, \(\overrightarrow{A^{\prime} B^{\prime}}\) is the image of \(\overrightarrow{A B}\) under a dilation from point O with an unknown scale factor; A maps to A’, and B maps to B’. Use direct measurement to determine the scale factor r, and then find the center of dilation O.
Answer:
Question 3.
Draw a line \(\overleftrightarrow{A B}\) and dilate points A and B from center O where O is not on \(\overleftrightarrow{A B}\). Use your diagram to explain why a line maps to a line under a dilation with scale factor r.
Answer:
Question 4.
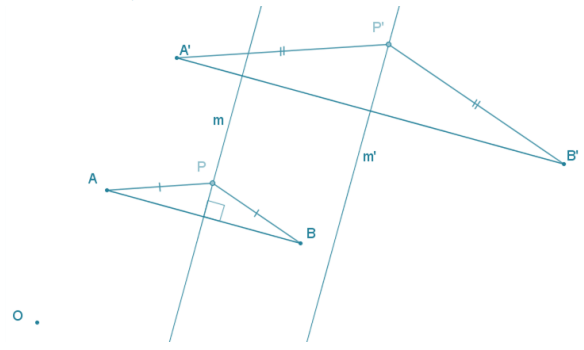
Let \(\overline{A B}\) be a line segment, and let m be a line that is the perpendicular bisector of \(\overline{A B}\). If a dilation with scale factor r maps \(\overline{A B}\) to \(\overline{A^{\prime} B^{\prime}}\) (sending A to A’ and B to B’) and also maps line m to line m’, show that line m’ is the perpendicular bisector of \(\overline{A^{\prime} B^{\prime}}\).
Answer:
Let P be a point on line m, and let the dilation send P to the point P’ on line m’. Since P is on the perpendicular bisector of \(\overline{A B}\), PA = PB. By the dilation theorem, P’A’ = rPA and P’B’ = rPB. So, P’A’ = P’B’, and P’ is on the perpendicular bisector of \(\overline{A^{\prime} B^{\prime}}\).
Question 5.
Dilate circle C with radius CA from center O with a scale factor r = \(\frac{1}{2}\).
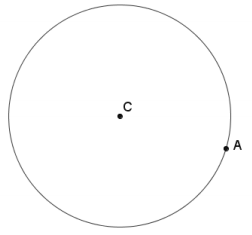
Answer:
Question 6.
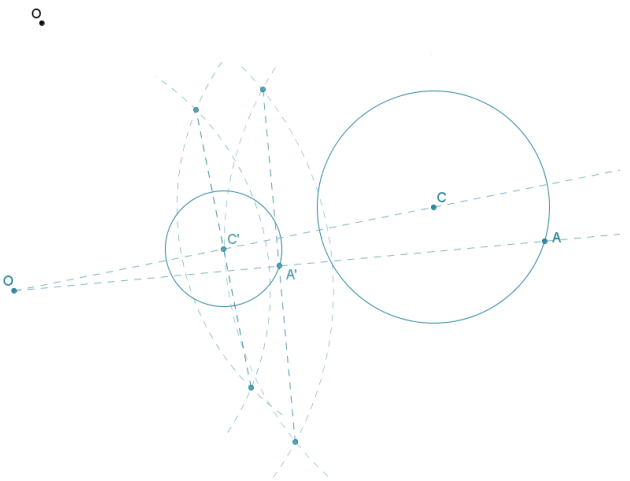
In the picture below, the larger circle is a dilation of the smaller circle. Find the center of dilation O.
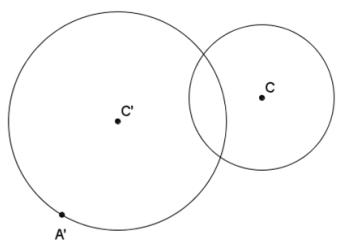
Answer:
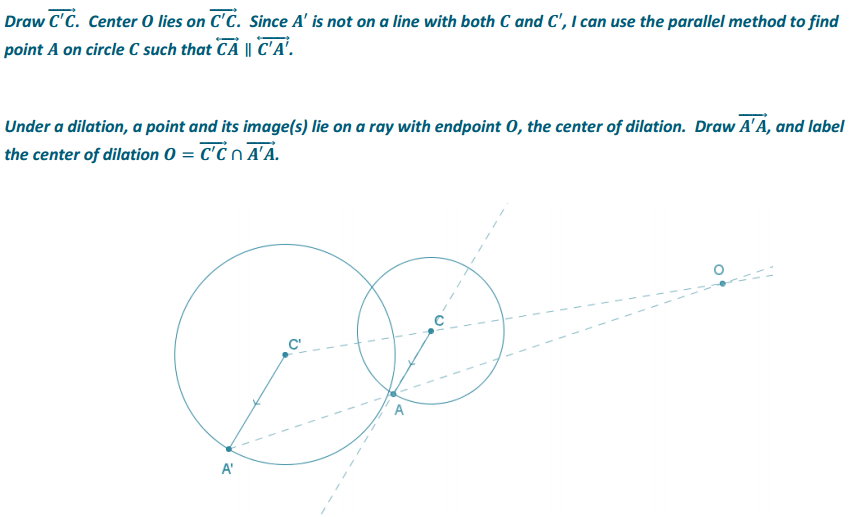
Eureka Math Geometry Module 2 Lesson 8 Exit Ticket Answer Key
Given Points O, S, and T below, complete parts (a) – (e):
Answer:
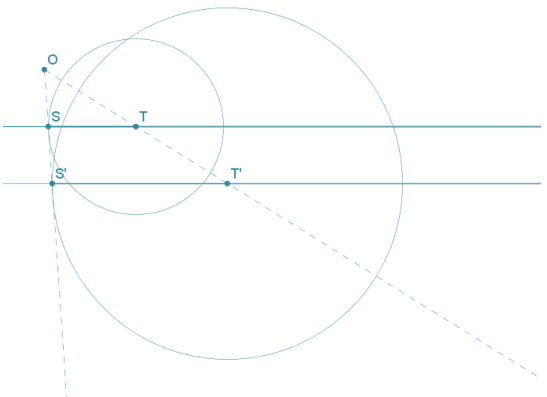
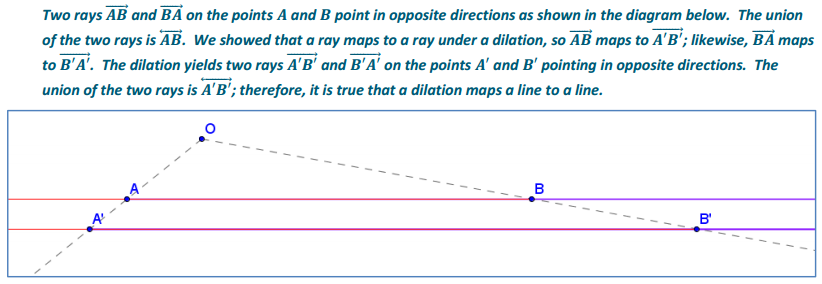
a. Draw rays \(\overrightarrow{S T}\) and \(\overrightarrow{T S}\). What is the union of these rays?
Answer:
The union of \(\overrightarrow{S T}\) and \(\overrightarrow{T S}\) is line ST.
b. Dilate \(\overrightarrow{S T}\) from O using scale factor r = 2. Describe the image of \(\overrightarrow{S T}\).
Answer:
The image of \(\overrightarrow{S T}\) is \(\overrightarrow{S^{\prime} T^{\prime}}\)
c. Dilate from \(\overrightarrow{T S}\) using scale factor r = 2. Describe the image of \(\overrightarrow{T S}\).
Answer:
The image of \(\overrightarrow{T S}\) is \(\overrightarrow{T^{\prime} S^{\prime}}\)
d. What does the dilation of the rays in parts (b) and (c) yield?
Answer:
The dilation of rays \(\overrightarrow{S T}\) and \(\overrightarrow{T S}\) yields \(\overleftrightarrow{\boldsymbol{S}^{\prime} \boldsymbol{T}^{\prime}}\).
e. Dilate circle C with radius TS from O using scale factor r = 2.
Answer:
See diagram above.