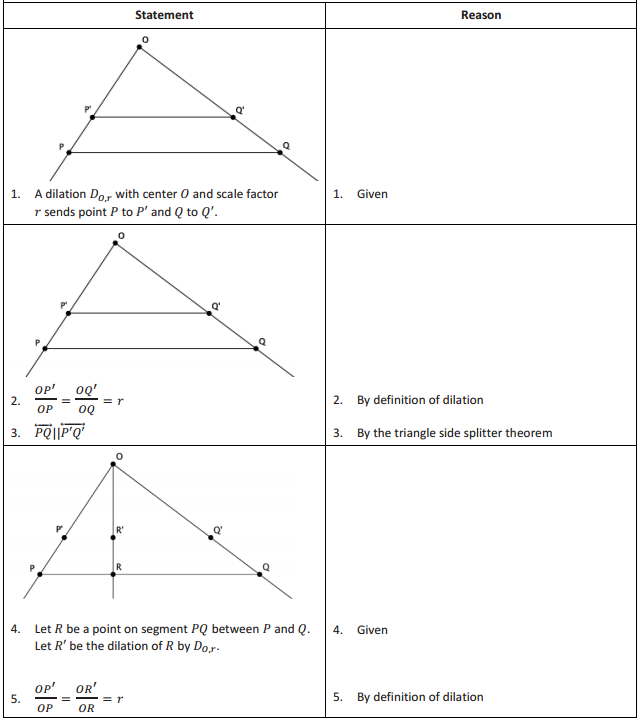
Engage NY Eureka Math Geometry Module 2 Lesson 7 Answer Key
Eureka Math Geometry Module 2 Lesson 7 Example Answer Key
Example 1.
Case 1. Consider the case where the scale factor of dilation is r = 1. Does a dilation from center O map segment PQ to a segment P’Q’? Explain.
Answer:
A scale factor of r = 1 means that the segment and its ima ge are equal. The dilation does not enlarge or shrink the image of the figure; it remains unchanged. Therefore, when the scale factor of dilation is r = 1, then the dilation maps the segment to itself.
Example 2.
Case 2. Consider the case where a line PQ contains the center of the dilation. Does a dilation from the center with scale factor r ≠1 map the segment PQ to a segment P’Q’? Explain.
Answer:
Yes. The dilation sends points P and Q to points P’ and Q’. Since the points P and Q are collinear with the center O, then both P’ and Q’ are also collinear with the center O. The dilation also takes all of the points between P and Q to all of the points between P’ and Q’ (again because their images must fall on the rays OP and OQ). Therefore, the dilation maps \(\overline{P Q}\) to \(\overline{P^{\prime} Q^{\prime}}\).
Example 3.
Case 3. Consider the case where 
does not contain the center O of the dilation, and the scale factor r of the dilation is not equal to 1; then, we have the situation where the key points O, P, and Q form ∆ OPQ. The scale factor not being equal to 1 means that we must consider scale factors such that 0 < r < 1 and r > 1. However, the proofs for each are similar, so we focus on the case when 0 < r < 1.
When we dilate points P and Q from center O by scale factor 0 < r < 1, as shown, what do we know about points P’ and Q’?
Answer:
We know P’ lies on ray OP with OP’ = r ∙ OP. and Q’ lies on ray OQ with OQ’ = r ∙ OQ. So, \(\frac{O P^{\prime}}{O P}=\frac{O Q^{\prime}}{O Q}\) = r. The line segment P’Q’ splits the sides of ∆ OPQ proportionally.
By the triangle side splitter theorem, we know that the lines containing \(\overline{P Q}\) and \(\overline{P^{\prime} Q^{\prime}}\) are parallel.
We use the fact that the line segment P’Q’ splits the sides of ∆ OPQ proportionally and that the lines containing \(\overline{P Q}\) and \(\overline{P^{\prime} Q^{\prime}}\) are parallel to prove that a dilation maps segments to segments. Because we already know what happens when points P and Q are dilated, consider another point R that is on the segment PQ. After dilating R from center O by scale factor r to get the point R’, does R’ lie on the segment P’Q’?
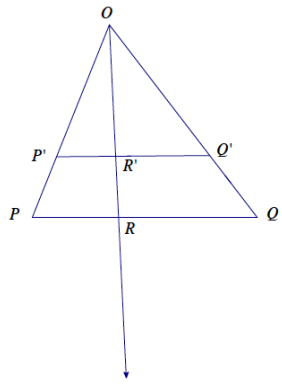
Answer:
Marwa’s proof of the statement: Let O be a point not on and Do,r be a dilation with center O and scale factor
0 < r < 1 that sends point P to P’ and Q to Q’. If R is another point that lies on , then Do,r(R) is a point that lies on 
.
There are still two subtle steps that need to be proved to show that dilations map segments to segments when the center does not lie on the line through the segment. The teacher may decide whether to show how to prove these two steps or just claim that the steps can be shown to be true. Regardless, the steps should be briefly discussed as part of what is needed to complete the proof of the full statement that dilations map segments to segments.
The first additional step that needs to be shown is that points on \(\overline{P Q}\) are sent to points on \(\overline{P^{\prime} Q^{\prime}}\), that is, if R is between P and Q, then R’ is between P’ and Q’. To prove this, we first write out what it means for R to be between P and Q: P, R, and Q are different points on the same line such that PR + RQ = PQ. By the dilation theorem (Lesson 6), P’R’ = r ∙ PR, R’Q’ = r ∙ RQ, and P’Q’ = r ∙ PQ. Therefore,
P’R’ + R’Q’ = r ∙ PR + r ∙ RQ = r(PR + RQ) = r ∙ PQ = P’Q’
Hence, P’R’ + R’Q’ = R’Q’, and therefore R’ is between P’ and Q’.
The second additional step is to show that the dilation is an onto mapping, that is, for every point R’ that lies on \(\overline{P^{\prime} Q^{\prime}}\), there is a point R that lies on \(\overline{P Q}\) that is mapped to R’ under the dilation. To prove, we use the inverse dilation at center O with scale factor \(\frac{1}{r}\) to get the point R and then follow the proof above to show that R lies on \(\overline{P Q}\).
Example 4.
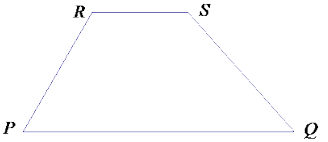
Since \(\overline{P Q}\) and \(\overline{R S}\) are segments of different lengths, then the non-base sides of the trapezoid are not parallel, and the lines containing them meet at a point O as shown.
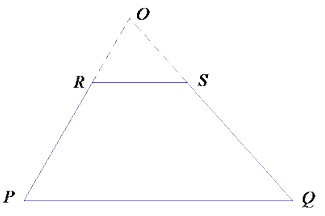
Recall that we want to show that a dilation maps \(\overline{P Q}\) to \(\overline{R S}\). Explain how to show it.
Answer:
The triangle formed with vertex O, ∆ OPQ, has PQ as its base. Since 
then the segment RS splits the sides of the triangle proportionally by the triangle side splitter theorem. Since we know the proportional side splitters of a triangle are the result of a dilation, then we know there is a dilation from center O by scale factor r that maps points P and Q to points R and S, respectively. Thus, a dilation maps \(\overline{P Q}\) to \(\overline{R S}\).
Eureka Math Geometry Module 2 Lesson 7 Opening Exercise Answer Key
a. Is a dilated segment still a segment? If the segment is transformed under a dilation, explain how.
Answer:
Accept any reasonable answer. The goal is for students to recognize that a segment dilates to a segment that is r times the length of the original.
b. Dilate the segment PQ by a scale factor of 2 from center O.
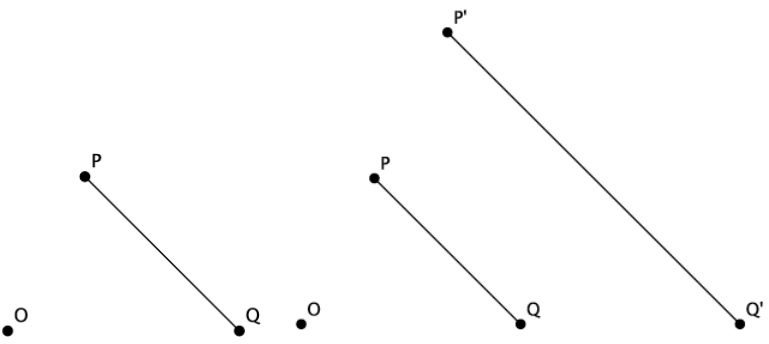
i. Is the dilated segment P’Q’ a segment?
Answer:
Yes, the dilation of segment PQ produces a segment P’Q’.
ii. How, if at all, has the segment PQ been transformed?
Answer:
Segment P’Q’ is twice the length of segment PQ. The segment has increased in length according to the scale factor of dilation.
Eureka Math Geometry Module 2 Lesson 7 Exercise Answer Key
In the following exercises, you will consider the case where the segment and its dilated image belong to the same line, that is, when \(\overline{P Q}\) and \(\overline{R S}\) are such that 
Exercise 1.
Consider points P, Q, R, and S on a line, where P = R, as shown below. Show there is a dilation that maps \(\overline{P Q}\) to \(\overline{R S}\). Where is the center of the dilation?
Answer:
If we assume there is a dilation that maps \(\overline{P Q}\) to \(\overline{R S}\), with a scale factor so that r = \(\frac{R S}{P Q}\), then the center of the dilation must coincide with endpoints P and R because, by definition of dilation, the center maps to itself. Since points P and R coincide, it must mean that the center O is such that O = P = R. Since the other endpoint Q of PQ
lies on 
, the dilated image of Q must also lie on the line (draw the ray from the center through point Q, and the ray coincides with ). Since the dilated image of Q must lie on the line, and point S is to the right of Q, then a dilation from center O with scale factor r > 1 maps \(\overline{P Q}\) to \(\overline{R S}\).
Exercise 2.
Consider points P, Q, R, and S on a line as shown below where \(\overline{P Q}\) ≠\(\overline{R S}\). Show there Is a dilation that maps \(\overline{P Q}\) to \(\overline{R S}\). Where is the center of the dilation?
Answer:
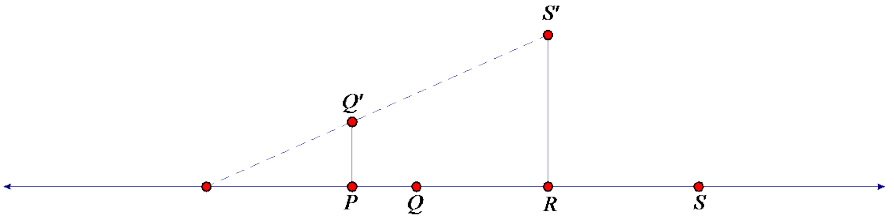
Construct perpendicular line segments of lengths PQ and RS through points P and R respectively. Note the endpoints of the perpendicular segments as Q’ and S’. Draw an auxiliary line through points Q’ and S’ that
intersects with 
. The intersection of the two lines is the center of dilation O. Since 
(perpendicular lines), by the triangle side splitter theorem, the segment PQ’ splits the triangle ∆ ORS’ proportionally, so by the dilation theorem, \(\frac{R S^{\prime}}{P Q^{\prime}}\) = r. This ratio implies that RS’ = r ∙ PQ’. By construction, PQ’ = PQ and RS’ = RS. Therefore,
RS = r ∙ PQ. By definition of dilation, since RS = r ∙ PQ, there is a dilation from center O with scale factor r that maps \(\overline{P Q}\) to \(\overline{R S}\).
Eureka Math Geometry Module 2 Lesson 7 Problem Set Answer Key
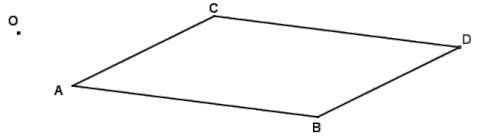
Question 1.
Draw the dilation of parallelogram ABCD from center O using the scale factor r = 2, and then answer the questions that follow.
Answer:
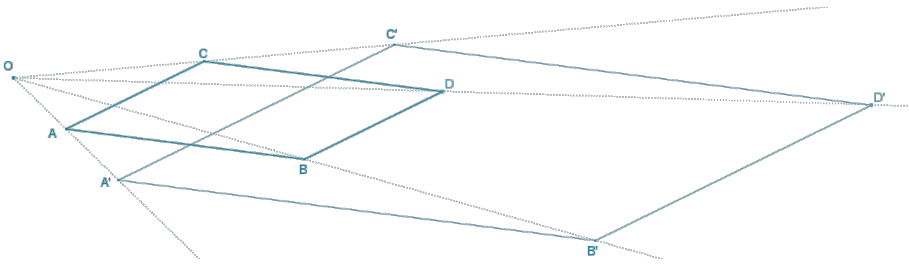
a. Is the image A’B’C’D’ also a parallelogram? Explain.
Answer:
b. What do parallel lines seem to map to under a dilation?
Answer:
Parallel lines map to parallel lines under dilations.
Question 2.
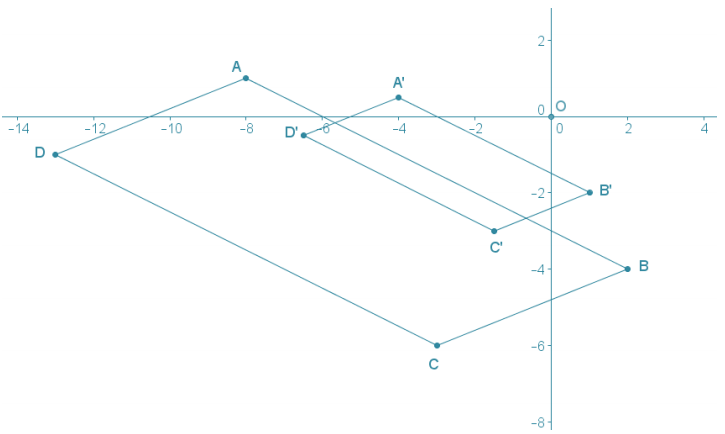
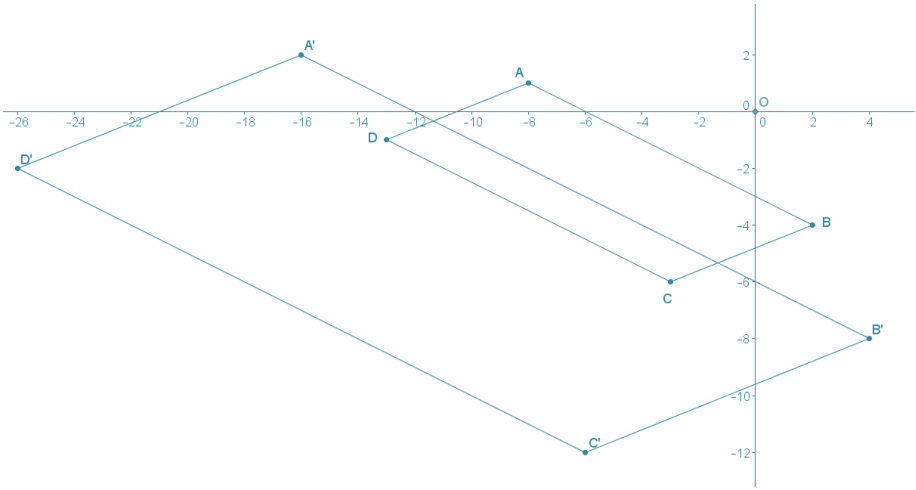
Given parallelogram ABCD with A(-8, 1), B(2, -4), C(-3, -6), and D(-13, -1), perform a dilation of the plane centered at the origin using the following scale factors.
a. Scale factor \(\frac{1}{2}\)
Answer:
b. Scale factor 2
Answer:
c. Are the images of parallel line segments under a dilation also parallel? Use your graphs to support your
answer.
The slopes of sides \(\overline{A B}\) and \(\overline{C D}\) in the original graph are –\(\frac{1}{2}\) and the slopes of each of the images of those sides under the dilations are also –\(\frac{1}{2}\) . The slopes of sides \(\overline{A D}\) and \(\overline{B C}\) in the original graph are \(\frac{2}{5}\), and the slopes of each of the ima ges of those sides under the dilations are also \(\frac{2}{5}\). This inform ally verifies that the images of parallel line segments are also parallel line segments.
Question 3.
In Lesson 7, Example 3, we proved that a line segment PQ, where O, P, and Q are the vertices of a triangle, maps to a line segment P’Q’ under a dilation with a scale factor r < 1. Using a similar proof, prove that for O not on 
a dilation with center O and scale factor r > 1 maps a point R on to a point R’ on line PQ.
Answer:
The proof follows almost exactly the same as the proof of Example 3, but using the following diagram instead:
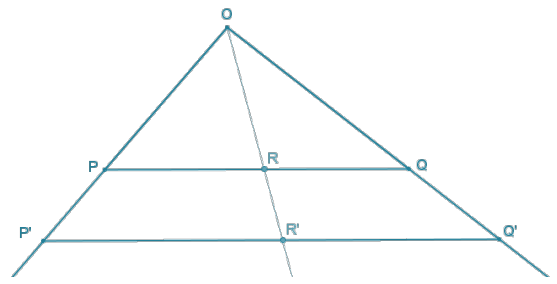
Question 4.
Answer:
Case 1: \(\overline{A B}\) and \(\overline{A^{\prime} B^{\prime}}\) are parallel directed line segments oriented in the same direction.
By the dilation theorem for segments, there is a dilation mapping A and B to A’ and B’, respectively.
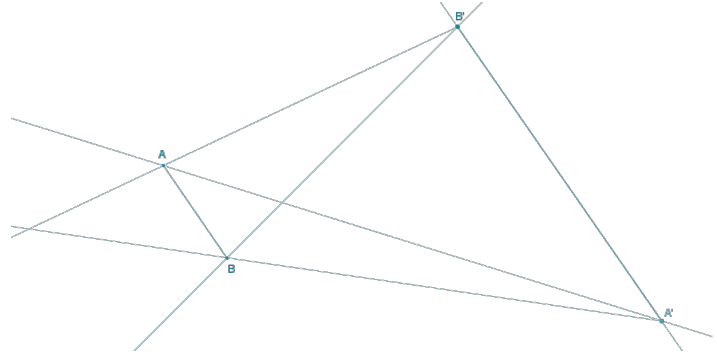
Case 2: \(\overline{A B}\) and \(\overline{A^{\prime} B^{\prime}}\) are parallel directed line segments oriented in the opposite directions.
We showed that directed line segments map to directed line segments that are oriented in the same direction, so there is a dilation mapping the parallel segments but only where the dilation maps A and B to B’ and A’, respectively.
Question 5.
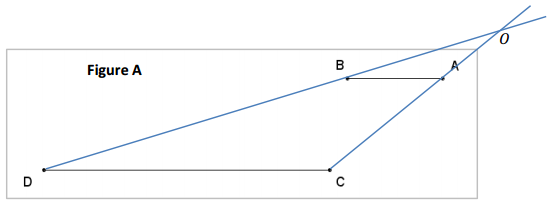
Only one of Figures A, B, or C below contains a dilation that maps A to A’ and B to B’. Explain for each figure why the dilation does or does not exist. For each figure, assume that 
.
a.
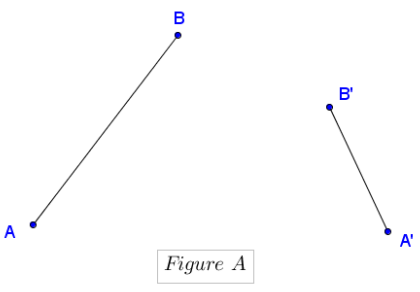
Answer:
b.
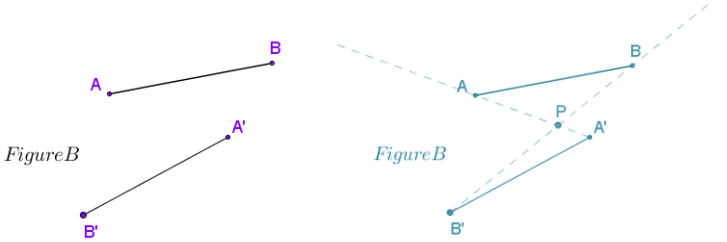
Answer:
c.
Answer:
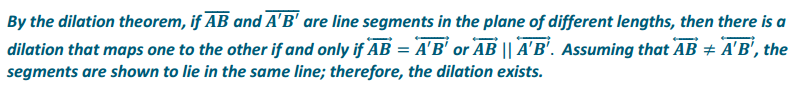
Eureka Math Geometry Module 2 Lesson 7 Exit Ticket Answer Key
Question 1.
Given the dilation \(D_{o, \frac{3}{2}}\) a line segment PQ, and that O is not on 
what can we conclude about the image of \(\overline{P Q}\)?
Answer:
Since P and Q are not in line with O, \(\overline{P^{\prime} Q^{\prime}}\) is parallel to \(\overline{P Q}\), and P’Q’ = \(\frac{3}{2}\)(P Q).
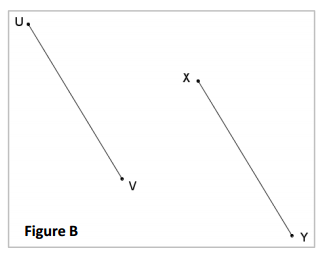
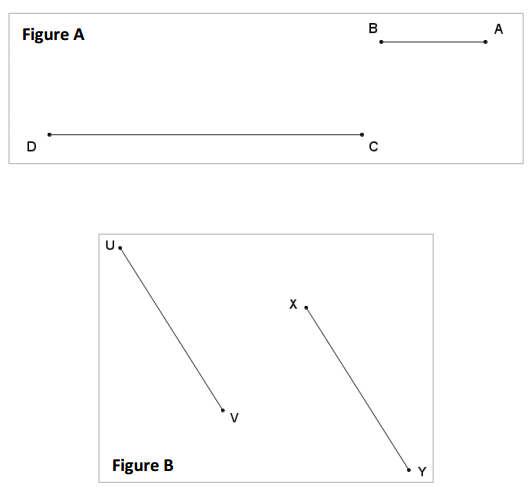
Question 2.
Given figures A and B below, \(\overline{B A}\|\overline{D C}, \overline{U V}\| \overline{X Y}\), and \(\overline{U V} \cong \overline{X Y}\), determine which figure has a dilation mapping the parallel line segments, and locate the center of dilation O. For one of the figures, a dilation does not exist. Explain why.
Answer:
