Engage NY Eureka Math Geometry Module 2 Lesson 30 Answer Key
Eureka Math Geometry Module 2 Lesson 30 Example Answer Key
Example 1.
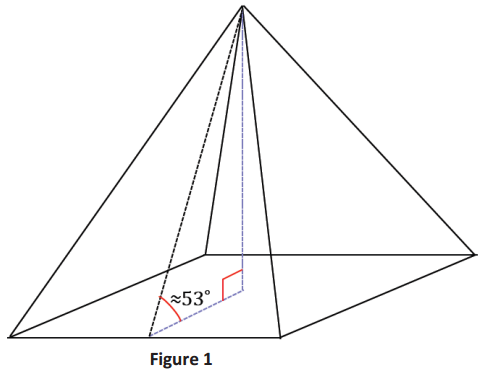
a. What common right triangle was probably modeled in the construction of the triangle in Figure 2? Use sin 53° ≈ 0.8.
Answer:
Right triangle with side lengths 3, 4, and 5, since 0.8 = \(\frac{4}{5}\).
→ What common right triangle was probably modeled in the construction of the triangle in Figure 2?
Though it may not be immediately obvious to students, part (a) is the same type of question as they completed in Exercises 1 – 2. The difference is the visual appearance of the value of sin 53 in decimal form versus in fraction form. Allow students time to sort through what they must do to answer part (a). Offer guiding questions and comments as needed such as the following:
→ Revisit Exercises 1 – 2. What similarities and differences do you notice between Example 1, part (a), and Exercises 1 – 2?
→ What other representation of 0.8 may be useful in this question?
Alternatively, students should also see that the value of sin S3° can be thought of as \(\frac{\text { opp }}{\text { hyp }}=\frac{0.8}{1}\). We proceed to answer part (a) using this fraction. If students have responses to share, share them as a whole class, or proceed to share the following solution:
→ To determine the common right triangle that was probably modeled in the construction of the triangle in Figure 2, using the approximation sin 53° ≈ 0.8 means we are looking for a right triangle with side-length relationships that are well known.
→ Label the triangle with given acute angle measure of approximately 53° as is labeled in the following figure. The hypotenuse has length 1, the opposite side has length 0.8, and the side adjacent to the marked angle is labeled as x.
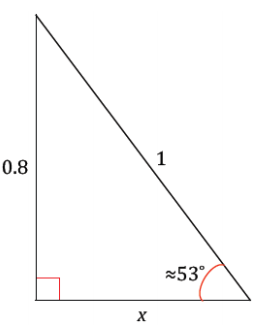
→ How can we determine the value of x?
We can apply the Pythagorean theorem.
→ Solve for x.
(0.8)2 + x2 = (1)2
0.64 + x2 = 1
x2 = 0.36
x = 0.6
→ The side lengths of this triangle are 0.6, 0.8, and 1. What well-known right triangle matches these lengths?
Even though the calculations to determine the lengths of the triangle have been made, determining that this triangle is a 3 – 4 – 5 triangle is still a jump. Allow time for students to persevere after the answer. Offer guiding questions and comments as needed such as the following:
→ Sketch a right triangle with side lengths 6, 8, and 10, and ask how that triangle is related to the one in the problem.
→ List other triangle side lengths that are in the same ratio as a 6 – 8 – 10 triangle.
Students should conclude part (a) with the understanding that a triangle with an acute angle measure of approximately 53° is a 3 – 4 – 5 triangle.
b. The actual angle between the base and lateral faces of the pyramid is actually closer to 52°. Considering the age of the pyramid, what could account for the difference between the angle measure in part (a) and the actual measure?
Answer:
The Great Pyramid is approximately 4,500 years old, and the weight of each block is several tons. It is conceivable that over time, the great weight of the blocks caused the pyramids to settle and shift the lateral faces enough so that the angle is closer to 52° than to 53°.
C. Why do you think the architects chose to use a 3 – 4 – 5 as a model for the triangle?
Answer:
Answers may vary. Perhaps they used it (1) because it is the right triangle with the shortest whole-number side lengths to satisfy the converse of the Pythagorean theorem and (2) because of the aesthetic it offers.
Example 2.
Show why tan θ = \(\frac{\sin \theta}{\cos \theta}\)
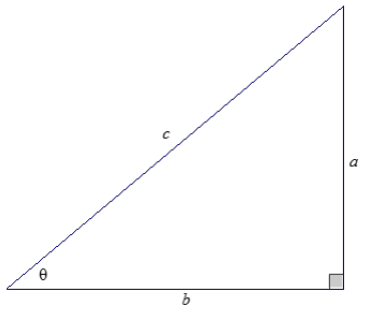
Answer:
Allow students time to work through the reasoning independently before guiding them through an explanation. To provide more support, consider having the diagram on the board and then writing the following to start students off:

tan θ = \(\frac{\sin \theta}{\cos \theta}\) because
sin θ = \(\frac{a}{c}\) and cos θ = \(\frac{b}{c}\).
Then,
tan θ = \(\frac{\sin \theta}{\cos \theta}\)
tan θ = \(\frac{a}{b}\), which is what we found earlier.
→ If you are given one of the values sin O, cos O, or tan 0, we can find the other two values using the identities
sin2 θ + cos2 θ = 1 and tan θ = \(\frac{\sin \theta}{\cos \theta}\) or by using the Pythagorean theorem.
Eureka Math Geometry Module 2 Lesson 30 Exercise Answer Key
Exercise 1.
In a right triangle with acute angle of measure θ, sin θ = \(\frac{1}{2}\). What is the value of cos θ? Draw a diagram as part of your response.
Answer:
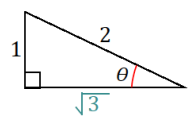
cos θ = \(\frac{\sqrt{3}}{2}\)
Exercise 2.
In a right triangle with acute angle of measure θ, sin θ = \(\frac{7}{9}\) What is the value of tan θ? Draw a diagram as part of your response.
Answer:
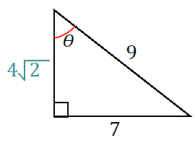
tan θ = \(\frac{7}{4 \sqrt{2}}=\frac{7 \sqrt{2}}{8}\)
Exercise 3.
In a right triangle with acute angle of measure θ, sin θ = \(\frac{1}{2}\), use the Pythagorean identity to determine the value of cos θ.
Answer:
sin2θ + cos2θ = 1
\(\left(\frac{1}{2}\right)^{2}\) + cos2θ = 1
\(\frac{1}{4}\) + cos2θ = 1
cos2θ = \(\frac{3}{4}\)
cos θ = \(\frac{\sqrt{3}}{2}\)
Exercise 4.
Given a right triangle with acute angle of measure θ, sin θ = \(\frac{7}{9}\) use the Pythagorean identity to determine the value of tan θ.
Answer:
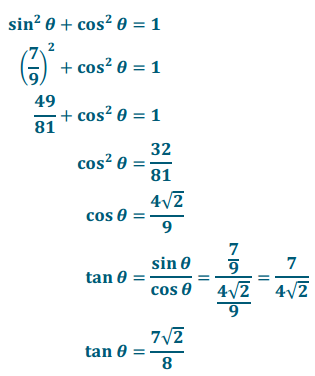
Eureka Math Geometry Module 2 Lesson 30 Problem Set Answer Key
Question 1.
If cos θ = \(\frac{4}{5}\), find sin θ and tan θ.
Answer:

Question 2.
If sin θ = \(\frac{44}{125}\), find cos θ and tan θ.
Answer:
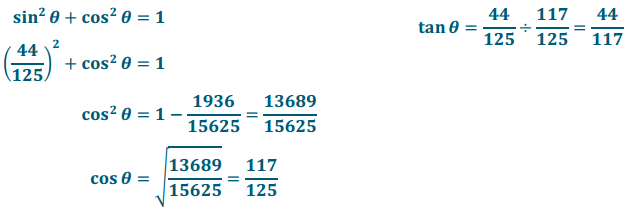
Question 3.
If tan θ = 5, find sin θ and cos θ.
Answer:
tan θ = 5 = \(\frac{5}{1}\), so the legs of a right triangle can be considered to have lengths of 5 and 1. Using the Pythagorean
theorem:
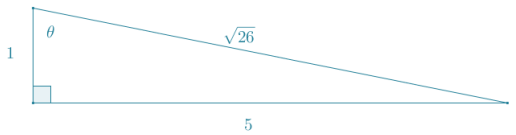
52 + 12 = hyp2
26 = hyp2
√26 = hyp
sin θ = \(\frac{5}{\sqrt{26}}=\frac{5 \sqrt{26}}{26}\); cos θ = \(\frac{1}{\sqrt{26}}=\frac{\sqrt{26}}{26}\)
Question 4.
If sin θ = \(\frac{\sqrt{5}}{5}\), find cos θ and tan θ.
Answer:

Question 5.
Find the missing side lengths of the following triangle using sine, cosine, and/or tangent. Round your answer to four decimal places.
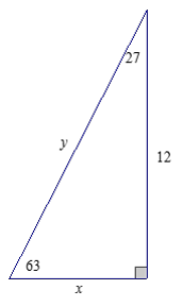
Answer:
\(\frac{x}{12}\) = tan 27
x = 12 tan 27 ≈ 6.1143
\(\frac{12}{y}\) = sin 63
y = \(\frac{12}{\sin 63}\) ≈ 13.4679
Question 6.
A surveying crew has two points A and B marked along a roadside at a distance of 400 yd. A third point C is marked at the back corner of a property along a perpendicular to the road at B. A straight path joining C to A forms a 28° angle with the road. Find the distance from the road to point C at the back of the property and the distance from A to C using sine, cosine, and/or tangent. Round your answer to three decimal places.
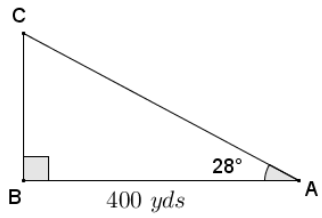
Answer:
tan 28 = \(\frac{B C}{400}\)
BC = 400(tan28)
BC ≈ 212. 684
The distance from the road to the back of the property is approximately 212.684 yd.
cos 28 = \(\frac{400}{A C}\)
AC = \(\frac{400}{\cos 28}\)
AC ≈ 453.028
The distance from point C to point A is approximately 453.028 yd.
Question 7.
The right triangle shown is taken from a slice of a right rectangular pyramid with a square base.
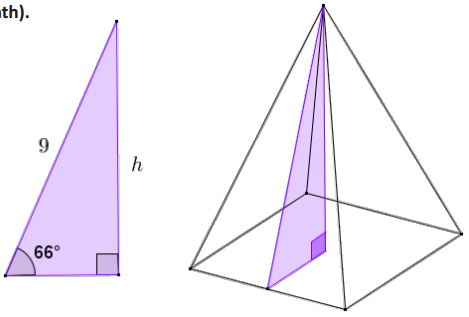
a. Find the height of the pyramid (to the nearest tenth).
Answer:
sin 66 = \(\frac{h}{9}\)
h = 9(sin 66)
h ≈ 8.2
The height of the pyramid is approximately 8.2 units.
b. Find the lengths of the sides of the base of the pyramid (to the nearest tenth).
Answer:
The lengths of the sides of the base of the pyramid are twice the length of the short leg of the right triangle shown.
cos 66 = \(\frac{n}{9}\)
n = 9(cos 66)
length = 2(9 cos 66)
length = 18 cos 66
length ≈ 7.3
The lengths of the sides of the base are approximately 7.3 units.
c. Find the lateral surface area of the right rectangular pyramid.
Answer:
The faces of the prism are congruent isosceles triangles having bases of 18 cos 66 and height of 9.
Area = \(\frac{1}{2}\) bh
Area = \(\frac{1}{2}\) (18 cos 66)(9)
Area = 81 cos 66
Area ≈ 32.9
The lateral surface area of the right rectangular pyramid is approximately 32.9 square units.
Question 8.
A machinist is fabricating a wedge in the shape of a right triangular prism. One acute angle of the right triangular base is 33°, and the opposite side is 6.5 cm. Find the length of the edges labeled l and m using sine, cosine, and/or tangent. Round your answer to the nearest thousandth of a centimeter.
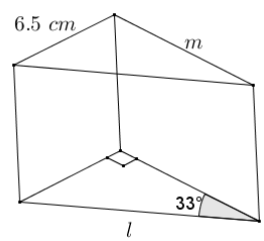
Answer:
sin 33 = \(\frac{6.5}{l}\)
l = \(\frac{6.5}{\sin 33}\)
l ≈ 11. 935
Distance l is approximately 11.935 cm.
tan 33 = \(\frac{6.5}{m}\)
m = \(\frac{6.5}{\tan 33}\)
m ≈ 10.009
Distance m is approximately 10.009 cm.
Question 9.
Let sin θ = \(\frac{1}{m}\) where 1, m > 0. Express tan θ and cos θ in terms of l and m.
Answer:

Eureka Math Geometry Module 2 Lesson 30 Exit Ticket Answer Key
Question 1.
If sin β = \(\frac{4 \sqrt{29}}{29}\), use trigonometric identities to find cos β and tan β.
Answer:
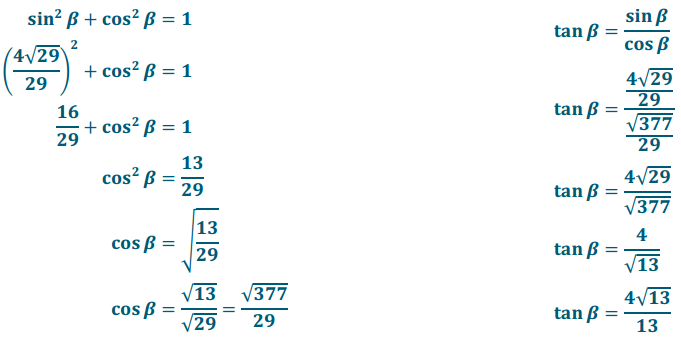
Question 2.
Find the missing side lengths of the following triangle using sine, cosine, and/or tangent. Round your answer to four decimal places.
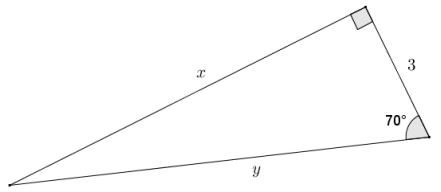
Answer:
cos 70 = \(\frac{3}{y}\)
y = \(\frac{3}{\cos 70}\) ≈ 8.7714
tan 70 = \(\frac{x}{3}\)
x = 3(tan 70) ≈ 8. 2424