Eureka Math Geometry Module 2 Lesson 24 Answer Key

Engage NY Eureka Math Geometry Module 2 Lesson 24 Answer Key

Eureka Math Geometry Module 2 Lesson 24 Exercise Answer Key

Exercise 1.
Find the length of the hypotenuse of a right triangle whose legs have lengths 50 and 100.
Answer:
c² = 50² + 100²
c² = 2500 + 10000
c² = 12500
√c² = √12500
c = \(\sqrt{2^{2} \cdot 5^{5}}\)
c = 2 · 5² √5
c = 50√5

Exercise 2.
Can you think of a simpler method for finding the length of the hypotenuse in Exercise 1? Explain.
Answer:
Accept any reasonable methods. Students may recall from Grade 8 that they can use what they know about similar triangles and scale factors to make their computations easier.

Exercise 3.
Find the length of the hypotenuse of a right triangle whose legs have lengths 75 and 225.
Answer:
A right triangle with leg lengths 75 and 225 has leg lengths that are 75 times longer than a triangle with leg lengths 1 and 3. A triangle with leg lengths 1 and 3 has a hypotenuse of length √10. Therefore, the length of the hypotenuse of a triangle with leg lengths 75 and 225 is 75√10.

Exploratory Challenge/Exercise 4-5

Exercise 4.
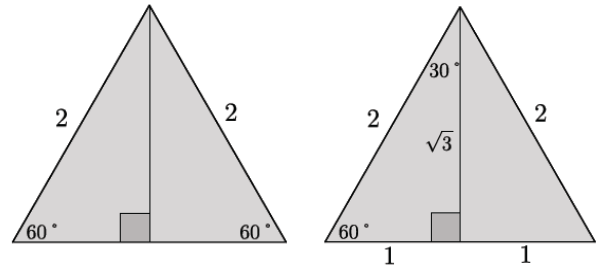
An equilateral triangle has sides of length 2 and angle measures of 60°, as shown below. The altitude from one vertex to the opposite side divides the triangle into two right triangles.
a. Are those triangles congruent? Explain.

Answer:
Yes, the two right triangles are congruent by ASA. Since the altitude is perpendicular to the base, then each of the right triangles has angles of measure 90° and 60°. By the triangle sum theorem, the third angle has a measure of 30°. Then, each of the right triangles has corresponding angle measures of 30° and 60°, and the included side length is 2.

b. What is the length of the shorter leg of each of the right triangles? Explain.
Answer:
Since the total length of the base of the equilateral triangle is 2, and the two right triangles formed are congruent, then the bases of each must be equal in length. Therefore, the length of the base of one right triangle is 1.

c. Use the Pythagorean theorem to determine the length of the altitude.
Answer:
Let h represent the length of the altitude.
1² + h² = 2²
h² = 2² – 1²
h² = 3
h = √3

d. Write the ratio that represents shorter leg: hypotenuse.
Answer:
1: 2

e. Write the ratio that represents longer leg: hypotenuse.
Answer:
√3: 2

f. Write the ratio that represents shorter leg: longer leg.
Answer:
1: √3

g. By the AA criterion, any triangles with measures 30 – 60 – 90 will be similar to this triangle. If a 30 – 60 – 90 triangle has a hypotenuse of length 16, what are the lengths of the legs?

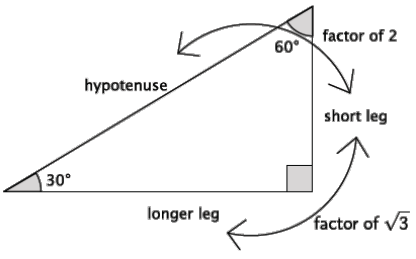
Answer:
Consider providing the following picture for students:
Let a represent the length of the shorter leg.
\(\frac{a}{16}=\frac{1}{2}\)
a = 8

Let b represent the length of the longer leg.
\(\frac{b}{16}=\frac{\sqrt{3}}{2}\)
2b = 16√3
b = 8√3

The length a = 8, and the length b = 8√3.

Note: After finding the length of one of the legs, some students may have used the ratio shorter leg: longer leg to determine the length of the other leg.

Exercise 5.
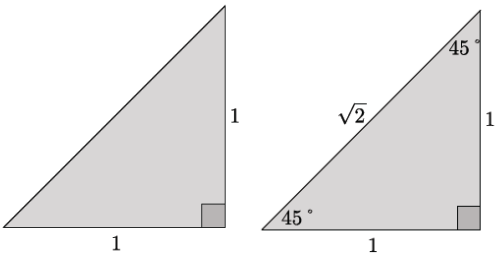
An isosceles right triangle has leg lengths of 1, as shown.
a. What are the measures of the other two angles? Explain.

Answer:
Base angles of an isosceles triangle are equal; therefore, the other two angles have a measure of 45°.

b. Use the Pythagorean theorem to determine the length of the hypotenuse of the right triangle.
Answer:
Let c represent the length of the hypotenuse.
1² + 1² = c²
2 = c²
√2 = c

c. Is It necessary to write all three ratios: shorter leg: hypotenuse, longer leg: hypotenuse, and shorter leg: longer leg? Explain.
Answer:
No, it is not necessary to write all three ratios. The reason is that the shorter leg and the longer leg are the same length. Therefore, the ratios shorter leg: hypotenuse and longer leg: hypotenuse will be the same. Additionally, the shorter leg: longer leg ratio would be 1: 1, which is not useful since we are given that the right triangle is an isosceles right triangle.

d. Write the ratio that represents leg: hypotenuse.
Answer:
1: √2

e. By the AA criterion, any triangles with measures 45 – 45 – 90 will be similar to this triangle. If a 45 – 45 – 90 triangle has a hypotenuse of length 20, what are the lengths of the legs?
Answer:
Let a represent the length of the leg.

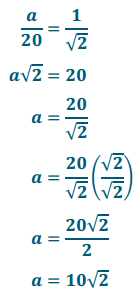
Eureka Math Geometry Module 2 Lesson 24 Problem Set Answer Key

Question 1.
In each row of the table below are the lengths of the legs and hypotenuses of different right triangles. Find the missing side lengths In each row, In simplest radical form.

Leg1	Leg2	Hypotenuse
15		25
15	36
3		7
100	200

Answer:

Leg1	Leg2	Hypotenuse
15	20	25
15	36	39
3	2√10	7
100	200	100√5

Answers provided in table
By the Pythagorean theorem:
leg₁² + leg₁² = hyp²
15² + y² = 25²
225 + y² = 625
y² = 400
y = 20 or y = – 20
The case where y = – 20 does not make sense since it represents a length of a side of a triangle and Is, therefore, disregarded.

Alternative strategy:
Divide each side length by the greatest common factor to get the side lengths of a similar right triangle. Find the missing side length for the similar triangle, and multiply by the GCF.

Leg: 15, Hypotenuse: 25, GCF(15, 25) = 5
Consider the triangle with Leg: 3 and Hypotenuse: 5. This Is a 3-4-5 right triangle. The missing leg length is 5 · 4 = 20.

Legs: 100 and 200: GCF(100, 200) = 100
Consider the right triangle with Legs: 1 and 2. Hypotenuse = √5. The missing hypotenuse length is 100√5.

Question 2.
Claude sailed his boat due south for 38 miles and then due west for 25 miles. Approximately how far is Claude from where he began?
Answer:

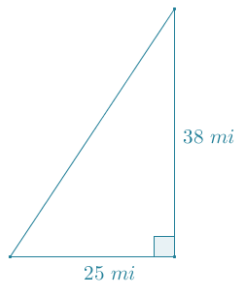
Claude’s path forms a right triangle since south and west are perpendicular to each other. His distance from where he began is a straight line segment represented by the hypotenuse of the triangle.
38² + 25² = hyp²
1444 + 625 = hyp2
2069 = hyp²
√2069 = hyp
Claude is approximately 45.5 miles from where he began.

Question 3.
Find the lengths of the legs in the triangle given the hypotenuse with length 100.

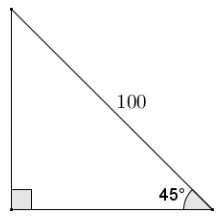
Answer:
By the Pythagorean theorem:
leg² + leg² = 100²
2 leg² 10000
leg² = 5000
leg = √5000
leg = √2500 √2
leg = 50√2

Alternative strategy:
The right triangle is an isosceles right triangle, so the leg lengths are equal. The hypotenuse of an isosceles right triangle can be calculated as follows:
hyp= leg · √2
100 = leg√2
\(\frac{100}{\sqrt{2}}\) = leg
\(\frac{100 \sqrt{2}}{2}\) = 50√2 = leg
The legs of the 45 – 45 – 90 right triangle with a hypotenuse of 100 are 50√2.

Question 4.
Find the length of the hypotenuse in the right triangle given that the legs have lengths of 100.

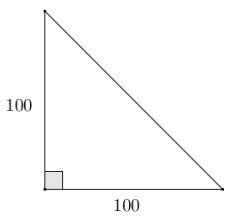
Answer:
By the Pythagorean theorem:
100² + 100² = hyp²
10000 + 10000 = hyp²
20000 = hyp²
√20000 = hyp
√10000 √2 = hyp²
100√2 = hyp

Alternative strategy:
The given right triangle is a 45 – 45 – 90 triangle. Therefore, the ratio of the length of its legs to the length of its hypotenuse is 1: √2
hyp = leg · √2
hyp = 100√2
The hypotenuse of the right triangle with legs of length 100 is 100√2.

Question 5.
Each row in the table below shows the side lengths of a different 30 – 60 – 90 right triangle. Complete the table with the missing side lengths in simplest radical form. Use the relationships of the values in the first three rows to complete the last row. How could the expressions in the last row be used?

Shorter Leg	Longer Leg	Hypotenuse
25		50
15
	3	2√3
x

Answer:

Shorter Leg	Longer Leg	Hypotenuse
25	25√3	50
15	15√3	30
√3	3	2√3
x	x√3	2x

The last row of the table shows that the sides of a 30 – 60 – 90 right triangle are multiples of 1, 2, and √3 by some constant x, with 2x being the longest and, therefore, the hypotenuse. The expressions could be used to find two unknown sides of a 30 – 60 – 90 triangle where only one of the sides is known.

Question 6.
In right triangle ABC with ∠C a right angle, an altitude of length h is dropped to side \(\overline{A B}\) that splits the side \(\overline{A B}\) into segments of length x and y. Use the Pythagorean theorem to show h² = xy.

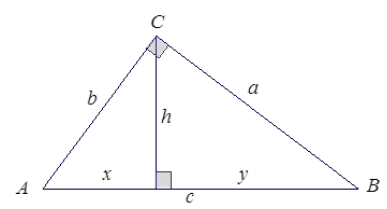
Answer:
By the Pythagorean theorem, a² + b² = C².
Since c = x + y, we have
a² + b² = (x + y)²
a² + b² = x² + 2xy + y².
Also by the Pythagorean theorem,
a² = h² + y², and b² = h² + x², so
a² + b² = h² + y² + h² + x²
a² + b² = 2h² + x² + y².
Thus, by substitution,
x² + 2xy + y² = 2h² + x² + y²
2xy = 2h²
xy = h².

Question 7.
In triangle ABC, the altitude from ∠C splits side \(\overline{A B}\) into two segments of lengths x and y. If h denotes the length of the altitude and h² = xy, use the Pythagorean theorem and its converse to show that triangle ABC is a right triangle with ∠C a right angle.

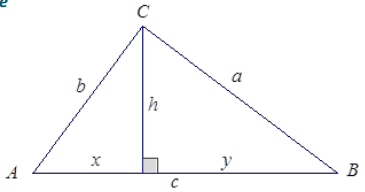
Answer:
Let a, b, and c be the lengths of the sides of the triangle opposite and ∠C, respectively. By the Pythagorean theorem:
a² = h² + y² and b² = h² + x², so
a² + b² = h² + y² + h² + x²
a² + b² = x² + 2h² + y²
a² + b² = x² + 2xy + y²
a² + b² = (x + y)²
a² + b² = c².
So, by the converse of the Pythagorean theorem, ∆ ABC is a right triangle, a and b are the lengths of legs of the triangle, and c is the hypotenuse, which lies opposite the right angle. Therefore, ∠C is the right angle of the right triangle.

Eureka Math Geometry Module 2 Lesson 24 Exit Ticket Answer Key

A right triangle has a leg with a length of 18 and a hypotenuse with a length of 36. Bernie notices that the hypotenuse is twice the length of the given leg, which means it is a 30 – 60 – 90 triangle. If Bernie is right, what should the length of the remaining leg be? Explain your answer. Confirm your answer using the Pythagorean theorem.
Answer:
A right angle and two given sides of a triangle determine a unique triangle. All 30 – 60 – 90 triangles are similar by AA criterion, and the lengths of their sides are 1c, 2c, and c√3 for some positive number c. The given hypotenuse is twice the length of the given leg of the right triangle, so Bernie’s conclusion is accurate. The ratio of the length of the short leg to the length of the longer leg of any 30 – 60 – 90 triangle is 1: √3 The given leg has a length of 18, which is \(\frac{1}{2}\) of the hypotenuse and, therefore, must be the shorter leg of the triangle.