Eureka Math Geometry Module 2 Lesson 22 Answer Key

Engage NY Eureka Math Geometry Module 2 Lesson 22 Answer Key

Eureka Math Geometry Module 2 Lesson 22 Exercise Answer Key

Simplify as much as possible.

Exercise 1.
√17² =
Answer:
√17² = 17

Exercise 2.
√5¹⁰ =
Answer:
\(\sqrt{5^{10}}=\sqrt{5^{2}} \times \sqrt{5^{2}} \times \sqrt{5^{2}} \times \sqrt{5^{2}} \times \sqrt{5^{2}}\)
= 5 × 5 × 5 × 5 × 5
= 5

Exercise 3.
√4x⁴ =
Answer:
\(\sqrt{4 x^{4}}=\sqrt{4} \times \sqrt{x^{2}} \times \sqrt{x^{2}}\)
= 2 × x × x
= 2|x|²

Exercise 4.
Complete parts (a) through (c). radical.
a. Compare the value of √36 to the value of √9 × √4.
Answer:
The value of the two expressions is equal. The square root of 36 is 6, and the product of the square roots of 9 and 4 is also 6.

b. Make a conjecture about the validity of the following statement: For nonnegative real numbers a and b, √ab = √a · √b. Explain.
Answer:
Answers will vary. Students should say that the statement √ab = √a · √b is valid because of the problem that was just completed: √36 = √9 × √4 = 6.

c. Does your conjecture hold true for a = – 4 and b = – 9?
Answer:
No. The conjecture is not true when the numbers are negative because we cannot take the square root of a negative number. \(\sqrt{(-4)(-9)}=\sqrt{36}\) = 6, but we cannot calculate \(\sqrt{-4} \times \sqrt{-9}\) in order to compare.

Exercise 5.
Complete parts (a) through (c).
a. Compare the value of \(\sqrt{\frac{100}{25}}\) to the value of \(\frac{\sqrt{100}}{\sqrt{25}}\).
Answer:
The value of the two expressions is equal. The fraction \(\frac{100}{25}\) simplifies to 4, and the square root of 4 is 2. The square root of 100 divided by the square root of 25 is equal to \(\frac{10}{5}\), which is equal to 2.

b. Make a conjecture about the validity of the following statement: For nonnegative real numbers a and b, when b ≠ 0, \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) . Explain.
Answer:
Answers will vary. Students should say that the statement \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) is valid because of the problem that was just completed: \(\sqrt{\frac{100}{25}}=\frac{\sqrt{100}}{\sqrt{25}}\) = 2.

c. Does your conjecture hold true for a = – 100 and b = – 25?
Answer:
No. The conjecture is not true when the numbers are negative because we cannot take the square root of a negative number. \(\sqrt{\frac{-100}{-25}}\) = √4 = 2, but we cannot calculate \(\frac{\sqrt{-100}}{\sqrt{-25}}\) in order to compare.

Simplify each expression as much as possible, and rationalize denominators when applicable.

Exercise 6.
√72 =
Answer:
√72 = √36 · √2
= 6√2

Exercise 7.
\(\sqrt{\frac{17}{25}}\) =
Answer:
\(\sqrt{\frac{17}{25}}=\frac{\sqrt{17}}{\sqrt{25}}\)
= \(\frac{\sqrt{17}}{5}\)

Exercise 8.
√32x =
Answer:
√32x = √16 √2x
= 4√2x

Exercise 9.
\(\sqrt{\frac{1}{3}}\)
Answer:

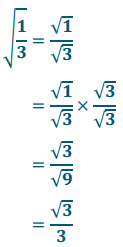
Exercise 10.
√54x² =
Answer:
√54x²= √9√6√x²
= 3|x|√6

Exercise 11.
\(\frac{\sqrt{36}}{\sqrt{18}}\) =
Answer:
\(\frac{\sqrt{36}}{\sqrt{18}}=\sqrt{\frac{36}{18}}\)
= √2

Exercise 12.
\(\sqrt{\frac{4}{x^{4}}}\) =
Answer:
\(\sqrt{\frac{4}{x^{4}}}=\frac{\sqrt{4}}{\sqrt{x^{4}}}\)
= \(\frac{2}{x^{2}}\)

Exercise 13.
\(\frac{4 x}{\sqrt{64 x^{2}}}\) =
Answer:
\(\frac{4 x}{\sqrt{64 x^{2}}}=\frac{4 x}{8 x}\)
= \(\frac{1}{2}\)

Exercise 14.
\(\frac{5}{\sqrt{x^{7}}}\) =
Answer:

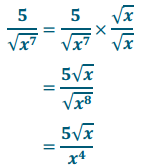
Exercise 15.
\(\sqrt{\frac{x^{5}}{2}}\)
Answer:

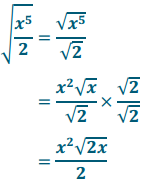
Exercise 16.
\(\frac{\sqrt{18 x}}{3 \sqrt{x^{5}}}\) =
Answer:

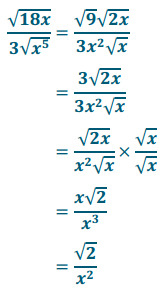
Exercise 17.
The captain of a ship recorded the ship’s coordinates, then sailed north and then west, and then recorded the new coordinates. The coordinates were used to calculate the distance they traveled, √578 km. When the captain asked how far they traveled, the navigator said, “About 24 km.” Is the navigator correct? Under what conditions might he need to be more precise in his answer?
Answer:
Sample student responses:
The number √578 is close to the perfect square √576. The perfect square √576 = 24; therefore, the navigator is correct in his estimate of the distance traveled.

When the number √578 is simplified, the result is 17√2. The number 578 has factors of 289 and 2. Then:
√578 = √289 √2
= 17√2
= 24.04163…
≈ 24
Yes, the navigator is correct in his estimate of the distance traveled.

A more precise answer may be needed if the captain were looking for a particular location, such as the location of a shipwreck or buried treasure.

Eureka Math Geometry Module 2 Lesson 22 Problem Set Answer Key

Question 1.
√6 · √60 =
Answer:
√6 · √60 = √6 · √6 · √10
= 6√10

Question 2.
√108 =
Answer:
√108 = √9 · √4 · √3
= 3 · 2√3
= 6√3

Question 3.
Pablo found the length of the hypotenuse of a right triangle to be √45. Can the length be simplified? Explain.
Answer:
√45 = √9√5
= 3√5
Yes, the length can be simplified because the number 45 has a factor that is a perfect square.

Question 4.
√12x⁴ =
Answer:
√12x⁴ = √4√3√x⁴
= 2x²√3

Question 5.
Sarahi found the distance between two points on a coordinate plane to be Can this answer be simplified? Explain.
Answer:
The number 74 can be factored, but none of the factors are perfect squares, which are necessary to simplify. Therefore, √74 cannot be simplified.

Question 6.
√16x³ =
Answer:
√16x³ = √16√x²√x
= 4x√x

Question 7.
\(\frac{\sqrt{27}}{\sqrt{3}}\) =
Answer:
\(\frac{\sqrt{27}}{\sqrt{3}}=\sqrt{\frac{27}{3}}\)
= √9
= 3

Question 8.
Nazem and Joff rey are arguing about who got the right answer. Nazem says the answer is \(\frac{1}{\sqrt{3}}\) and Joffrey says the answer is \(\frac{\sqrt{3}}{3}\). Show and explain that their answers are equivalent.
Answer:
\(\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{\sqrt{3}}{3}\)
If Nazem were to rationalize the denominator in his answer, he would see that it is equal to Joffrey’s answer.

Question 9.
\(\sqrt{\frac{5}{8}}\) =
Answer:

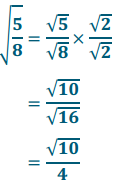
Question 10.
Determine the area of a square with side length 2√7 in.
Answer:
A = (2√7)²
= 2²(√7)²
= 4(7)
= 28
The area of the square is 28 in².

Question 11.
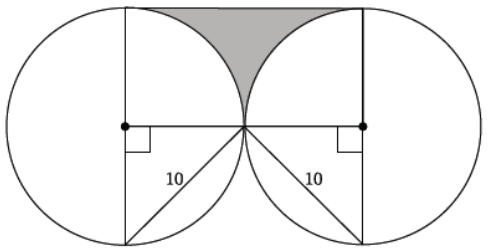
Determine the exact area of the shaded region shown below.

Answer:
Let r be the length of the radius.
By special triangles or the Pythagorean theorem, r = 5√2.
The area of the rectangle containing the shaded region is
A = 2(5√2) (5√2) = 2(25)(2) = 100.
The sum of the two quarter circles in the rectangular region is
A = \(\frac{1}{2}\)π(5√2)²
= \(\frac{1}{2}\) π(25)(2)
= 25π.
The area of the shaded region is 100 – 25π square units.

Question 12.
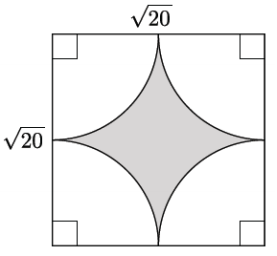
Determine the exact area of the shaded region shown to the right.

Answer:
The radius of each quarter circle is \(\frac{1}{2}\)(√20) = \(\frac{1}{2}\) (2√5) = √5.
The sum of the area of the four circular regions is A = π(√5)² = 5π.
The area of the square is A = (√20)² = 20.
The area of the shaded region is 20 – 5π square units.

Question 13.
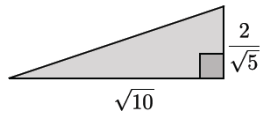
Calculate the area of the triangle to the right.

Answer:

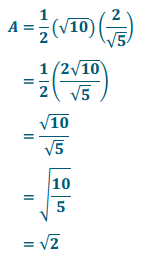
The area of the triangle is √2 square units.

Question 14.
\(\frac{\sqrt{2 x^{3}} \cdot \sqrt{8 x}}{\sqrt{x^{3}}}\) =
Answer:

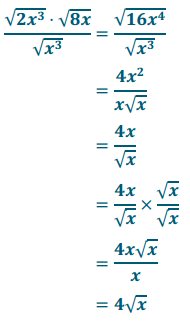
Question 15.
Prove Rule 2 for square roots: \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) (a ≥ 0, b > 0)
Let p be the nonnegative number so that p² = a, and let q be the nonnegative number so that q² = b. Then,
Answer:

Eureka Math Geometry Module 2 Lesson 22 Exit Ticket Answer Key

Question 1.
√243 =
Answer:
√243 = √81 · √3
= 9√3

Question 2.
\(\sqrt{\frac{7}{5}}\)
Answer:

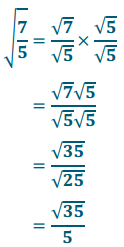
Question 3.
Teja missed class today. Explain to her how to write the length of the hypotenuse in simplest radical form.

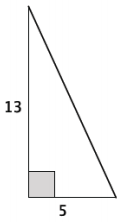
Answer:
Use the Pythagorean theorem to determine the length of the hypotenuse, C:
5² + 13² = c²
25 + 169 = c²
194 = c²
√194 = c
To simplify the square root, rewrite the radicand as a product of its factors. The goal is to find a factor that is a perfect square and can then be simplified. There are no perfect square factors of the radic and; therefore, the length of the hypotenuse in simplest radical form is √194.