Engage NY Eureka Math Geometry Module 2 Lesson 20 Answer Key
Eureka Math Geometry Module 2 Lesson 20 Example Answer Key
a. If the circumference of the earth is about 25,000 miles, what is the earth’s diameter in miles?
Answer:
\(\frac{25000}{\pi}\) ≈ 8000
The earth’s diameter is approximately 8,000 miles.
b. Using part (a), what is the moon’s diameter in miles?
Answer:
\(\frac{2}{7} \cdot \frac{25000}{\pi}\) ≈ 2300
The moon’s diameter is approximately 2,300 miles.
c. How far away is the moon in miles?
Answer:
\(108 \cdot \frac{2}{7} \cdot \frac{25000}{\pi}\) ≈ 246 000
The moon is approximately 246,000 miles from the earth.
Eureka Math Geometry Module 2 Lesson 20 Opening Exercise Answer Key
What is a solar eclipse? What is a lunar eclipse?
Answer:
A solar eclipse occurs when the moon passes between the earth and the sun, and a lunar eclipse occurs when the earth passes between the moon and the sun.
Discussion
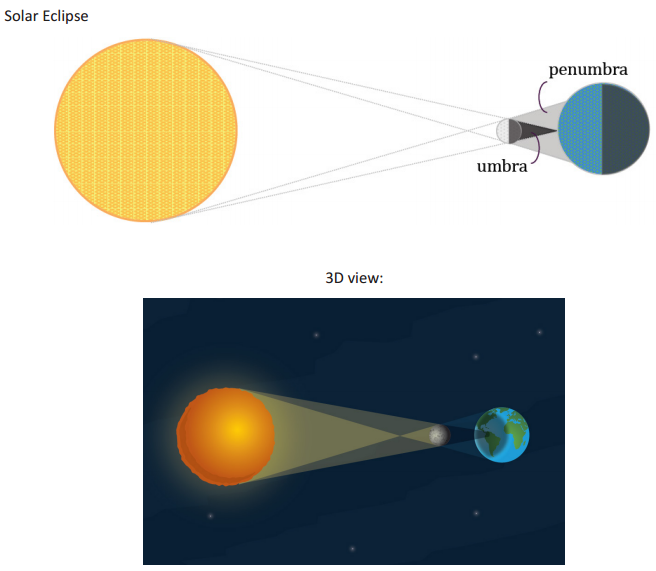
Answer:
Lead students through a conversation regarding the details of solar and lunar eclipses.
→ A total solar eclipse lasts only a few minutes because the sun and moon appear to be the same size.
→ How would appearances change if the moon were closer to the earth?
The moon would appear larger.
→ The moon would appear larger, and the eclipse would last longer. What if the moon were farther away from the earth? Would we experience a total solar eclipse?
The moon would appear smaller, and it would not be possible for a total solar eclipse to occur, because the moon would appear as a dark dot blocking only part of the sun.
→ Sketch a diagram of a solar eclipse.
Students’ knowledge on eclipses varies. This is an opportunity for students to share what they know regarding eclipses. Allow a minute of discussion, and then guide them through a basic description of the moon’s shadow and how it is conical (in 3D view), but on paper in a profile view, the shadow appears as an isosceles triangle whose base coincides with the diameter of the earth. Discuss what makes the shadows of celestial bodies similar. Describe the two parts of the moon’s shadow, the umbra and penumbra.
Note that the distances are not drawn to scale in the following image.
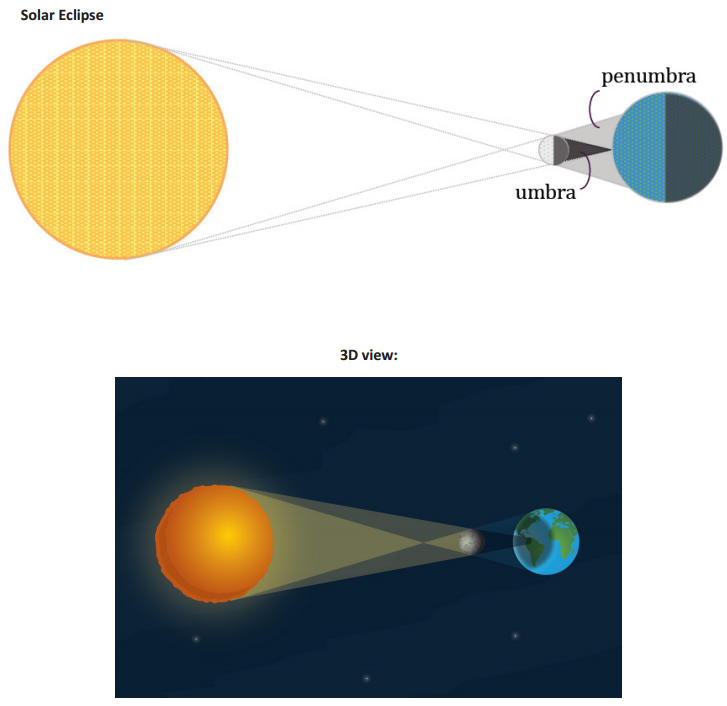
→ The umbra is the portion of the shadow where all sunlight is blocked, while the penumbra is the part of the shadow where light is only partially blocked. For the purposes of our discussion today, we will be simplifying the situation and considering only the umbra.
→ What is remarkable about the full shadow caused by the eclipse? That is, what is remarkable about the umbra and the portion of the moon that is dark? Consider the relationship between the 3D and 2D image of it.
If a cone represents the portion of the moon that is dark as well as the umbra, then the part that is entirely dark in the 2D image is an isosceles triangle.
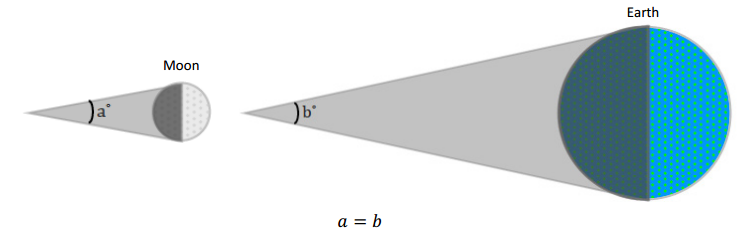
→ We assume that shadows from the moon and the earth are all similar isosceles triangles.
This is, in fact, not the case for all planetary objects, as the shadow formed depends on how far away the light source is from the celestial body and the size of the planet. For the sake of simplification as well as approximation, this assumption is made. Then, shadows created by the moon and the earth will have the following relationship:
→ You can imagine simulating a solar eclipse using a marble that is one inch in diameter. If you hold it one arm length away, it will easily block (more than block) the sun from one eye. Do not try this; you will damage your eye!
→ To make the marble just barely block the sun, it must be about 9 feet (i.e., 108 inches) away from your eye. So the cone of shadow behind the marble tapers to a point, which is where your eye is, and at this point, the marble just blocks out the sun. This means that the ratio of the length of the shadow of the marble to the diameter of the marble is about 108: 1.
→ In fact, by experimenting with different-size spheres, we find that this ratio holds true regardless of the size of the sphere (or circular object) as long as the sphere is at the point where it just blocks the sun from our vantage point. In other words, whether you are using a marble, a tennis ball, or a basketball to model the eclipse, the distance the sphere must be held from the eye is 108 times the diameter of the sphere.
→ We conclude that this ratio also holds for the moon and the earth during a solar eclipse. Since the moon and sun appear to be the same size in the sky (the moon just blocks the sun in a solar eclipse), we can conclude that the distance from the earth to the moon must also be roughly 108 times the diameter of the moon because the earth is at the tip of the moon’s shadow.
→ Let us now consider what is happening in a lunar eclipse. A lunar eclipse occurs when the moon passes behind the earth. Once again, the earth, sun, and moon lie on a straight line, but this time the earth is between the moon and the sun.
→ Consequently, during a lunar eclipse, the moon is still faintly visible from the earth because of light reflected off the earth.
→ Sketch a diagram of a lunar eclipse.
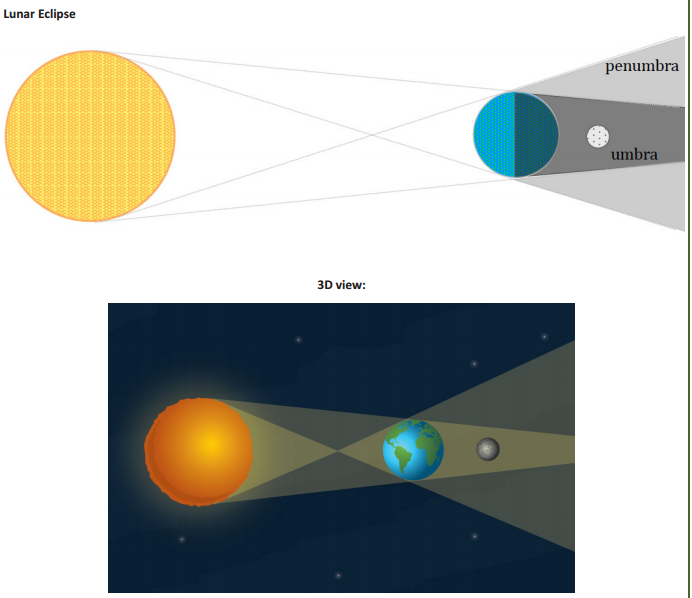
→ Based on what we know about the ratio of distances for an object to just block the sun, we can conclude that the moon must be within 108 earth diameters; if it were not within that distance, it would not pass through the earth’s shadow, and the earth could not block the sun out completely.
→ Studying total lunar eclipses was critical to finding the distance to the moon. Other types of eclipses exist, but they involve the penumbra. The following measurement required a total eclipse, or one involving the umbra.
→ By carefully examining the shadow of the earth during a total lunar eclipse, it was determined that the width, or more specifically, the diameter of the cross section of the earth’s conical shadow at the distance of the moon, is about 2\(\frac{1}{2}\). moon diameters.
→ With this measurement, a diagram like the following was constructed, where the shadow of the moon was reversed along the shadow of the earth:
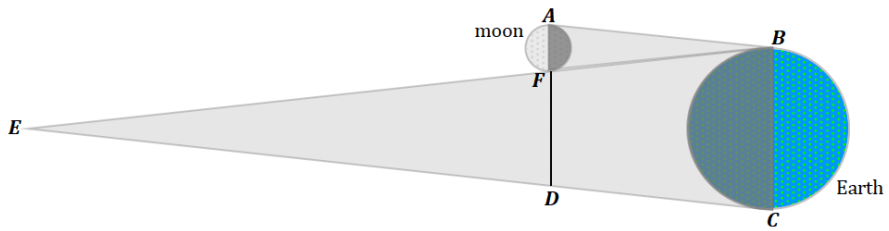
→ What length and angle relationships can we label in this diagram?
Pose the following questions one at a time, and allow students to discuss and mark their diagrams.
→ Based on what is known about the shadows of the moon and the earth, what do we know about the measures of ∠ABF and ∠BEC?
The angle measures are equal since we are assuming the shadows can be modeled by similar isosceles triangles.
→ What is the relationship between AF and AB?
Since the distance an object must be from the eye to block out the sun is 108 times the object’s diameter, the length of AB must be 108 times that of AF.
→ What is the relationship between AF and FD?
We know that the diameter of the cross section of the earth’s conical shadow at the distance of the moon is about 2\(\frac{1}{2}\) moon diameters, so the length of FD is 2.5 times the length of AF.
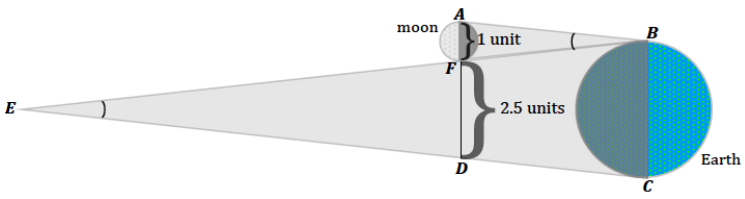
→ Reversing the moon’s shadow completes parallelogram ABCD. How can we be sure that ABCD is a parallelogram?
Allow students time to discuss why this must be true, using the relationships determined in the diagram. Share out ideas
before explaining further.
→ \(\overline{A D}\) must be parallel to \(\overline{B C}\) by construction. The diameter of the earth is parallel to the segment formed by the moon’s diameter and the diameter of the shadow at the distance of the moon.
→ We know that mz.ABF mz.BEC since the shadows are similar triangles. This means that \(\overline{A B}\) is parallel to \(\overline{D C}\) (alternate interior angles).
→ Since we know that ABCD is a parallelogram, then AD = BC, or BC = 3.5 units.
→ From our work in Lesson 19, we know the Greeks had the circumference of the earth at this time, which means they also had the earth’s diameter. Then, it was known that BC ≈ 8000 miles. With this information, we
conclude:
3.5 units ≈ 8000
1 unit ≈ 2300.
→ We already know that the distance from the moon to the earth is 108 times the diameter of the moon. If the moon has a diameter of approximately 2,300 miles, then the distance from the moon to the earth is roughly (2300 × 108) miles, or 248,000 miles.
→ With some careful observation and measurement (that of a lunar eclipse) and basic geometry, Aristarchus was able to determine a fairly accurate measure of the distance from the earth to the moon.
Eureka Math Geometry Module 2 Lesson 20 Problem Set Answer Key
Question 1.
If the sun and the moon do not have the same diameter, explain how the sun’s light can be covered by the moon during a solar eclipse.
Answer:
The farther away an object is from the viewer, the smaller that object appears. The moon is closer to the earth than the sun, and it casts a shadow where it blocks some of the light from the sun. The sun is much farther away from the earth than the moon, and because of the distance, it appears much smaller in size.
Question 2.
What would a lunar eclipse look like when viewed from the moon?
Answer:
The sun would be completely blocked out by the earth for a time because the earth casts an umbra that spans a greater distance than the diameter of the moon, meaning the moon would be passing through the earth’s shadow.
Question 3.
Suppose you live on a planet with a moon, where during a solar eclipse, the moon appears to be half the diameter of the sun.
a. Draw a diagram of how the moon would look against the sun during a solar eclipse.
Answer:
Sample response:

b. A 1-inch diameter marble held 100 inches away on the planet barely blocks the sun. How many moon diameters away Is the moon from the planet? Draw and label a diagram to support your answer.
Answer:
If the diameter of the moon appears to be half the diameter of the sun as viewed from the planet, then the moon will not cause a total eclipse of the sun. In the diagram, PQ is the diameter of the moon, and TU is the diameter of the sun as seen from the planet at point I.
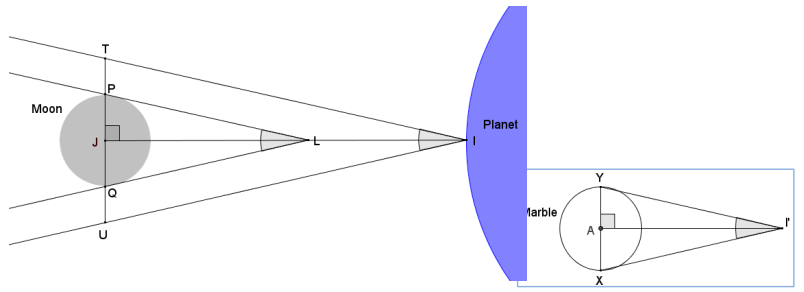
The diameter of the moon is represented by distance PQ. For me to view a total eclipse, where the sun is just blocked by the moon, the moon would have to be twice as wide, so TU = 2 (P Q). ∆ TIU and ∆ YI’X are both isosceles triangles, and their vertex angles are the same, so the triangles are similar by the SAS criterion.
If the triangles are similar, then their altitudes are in the same ratio as their bases. This means = \(\frac{I J}{T U}=\frac{I^{\prime} A}{Y X}\). By substituting values, \(\frac{I J}{2 P Q}=\frac{100}{1}\), so Ij = 200(PQ). The moon is approximately 200 moon diameters from the planet.
c. If the diameter of the moon is approximately \(\frac{3}{5}\) of the diameter of the planet and the circumference of the planet is 185,000 miles, approximately how far is the moon from the planet?
Answer:
The diameter of the planet:
dplanet = \(\frac{185000}{\pi}\)
dplanet = \(\frac{185000}{\pi}\)
The diameter of the planet is approximately 58,887 miles.
The diameter of the moon:
dmoon = \(\frac{3}{5}\) dplanet
dmoon = \(\frac{3}{5}\left(\frac{185000}{\pi}\right)\)
dmoon = \(\frac{111000}{\pi}\)
The diameter of the moon is approximately 35,332 miles.
The distance of the moon from the planet:
IJ = 200(PQ)
IJ = 200\(\left(\frac{111000}{\pi}\right)\)
IJ = \(\frac{22200000}{\pi}\)
The planet’s moon is approximately 7,066,479 miles from the planet.
Eureka Math Geometry Module 2 Lesson 20 Exit Ticket Answer Key
Question 1.
On Planet A, a\(\frac{1}{4}\)-inch diameter ball must be held at a height of 72 inches to just block the sun. If a moon orbiting
Planet A just blocks the sun during an eclipse, approximately how many moon diameters is the moon from the planet?
Answer:
The ratio of the diameter of the ball to the specified height is \(\frac{\frac{1}{4}}{72}=\frac{1}{288}\). The moon’s distance in order to just block the sun would be proportional since the shadows formed are similar triangles, so the moon would orbit approximately 288 moon diameters from Planet A.
Question 2.
Planet A has a circumference of 93,480 miles. Its moon has a diameter that is approximately \(\frac{1}{8}\) that of Planet A. Find the approximate distance of the moon from Planet A.
Answer:
To find the diameter of Planet A:
\(\frac{93480}{\pi}\) = dplanet A
The diameter of Planet A is approximately 29,756 miles.
To find the diameter of the moon:
dmoon = dp1anetA
dmoon = \(\frac{1}{8}\left(\frac{93480}{\pi}\right)\)
dmoon = \(\frac{93480}{8 \pi}=\frac{11685}{\pi}\)
The diameter of the moon is approximately 3,719 miles.
To find the distance of the moon from Planet A:
distancemoon = 288(dmoon)
distancemoon = 288\(\left(\frac{11685}{\pi}\right)\)
distancemoon = \(\frac{3365280}{\pi}\)
The distance from Planet A to its moon is approximately 1,071,202 miles.