Eureka Math Geometry Module 2 Lesson 18 Answer Key

Engage NY Eureka Math Geometry Module 2 Lesson 18 Answer Key

Eureka Math Geometry Module 2 Lesson 18 Opening Exercise Answer Key

a. What is an angle bisector?
Answer:
The bisector of an angle is a ray in the Interior of the angle such that the two adjacent angles formed by it have equal measures.

b. Describe the angle relationships formed when parallel lines are cut by a transversal.
Answer:
When parallel lines are cut by a transversal, the corresponding, alternate interior, and alternate exterior angles are all congruent; the same-side interior angles are supplementary.

c. What are the properties of an isosceles triangle?
Answer:
An isosceles triangle has at least two congruent sides, and the angles opposite to the congruent sides (i.e., the base angles) are also congruent.

Discussion

In the diagram below, the angle bisector of ∠A in ∆ ABC meets side \(\overline{B C}\) at point D. Does the angle bisector create any observable relationships with respect to the side lengths of the triangle?

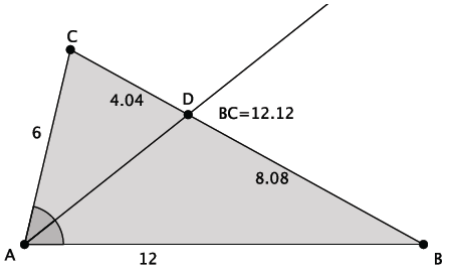
Answer:
Acknowledge any relationships students may find, but highlight the relationship BD: CD = BA: CA. Then, continue the discussion below that proves this relationship.

Eureka Math Geometry Module 2 Lesson 18 Exercise Answer Key

Exercise 1.
The sides of a triangle are 8, 12, and 15. An angle bisector meets the side of length 15. Find the lengths x and y. Explain how you arrived at your answers.

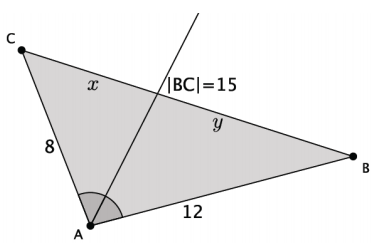
Answer:
\(\frac{y}{x}=\frac{12}{8}\)                  x = 15 – 9
x= 15 – y                 x = 6
8y = 12x
8y = 12(15 – y)
8y = 180 – 12y
20y = 180
y = 9
The length x is 6, and the length y is 9.

Since I know that ∠A is bisected, i applied what I knew about the angle bisector theorem to determine the lengths x and y. Specifically, the angle bisector cuts the side that is opposite the bisected angle so that y: x = 12:8. I set up an equation using the values of the ratios, which could be solved once I rewrote one of the variables x or y. I rewrote x as 15 – y and then solved for y. Once I had a value for y, I could replace it in the equation x = 15 – y to determine the value of X.

Exercise 2.
The sides of a triangle are 8, 12, and 15. An angle bisector meets the side of length 12. Find the lengths x and y.

Answer:
y = 12- x                  y = 12 – 4\(\frac{4}{23}\)
\(\frac{x}{12-x}=\frac{8}{15}\)                  y = 7\(\frac{19}{23}\)
15x = 8(12 – x)
15x = 96 – 8x
23x = 96
x = \(\frac{96}{23}=4 \frac{4}{23}\)
The length of x is 4\(\frac{4}{23}\) and the length of y is 7\(\frac{19}{23}\).

Exercise 3.
The sides of a triangle are 8, 12, and 15. An angle bisector meets the side of length 8. Find the lengths x and y.

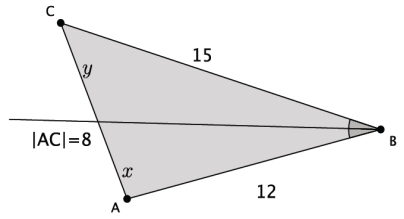
Answer:
\(\frac{y}{x}=\frac{15}{12}\)                  y = 8 – 3\(\frac{5}{9}\)
y = 8 – x                  y = 4\(\frac{4}{9}\)
15x = 12y
15x = 12(8-x)
15x = 96 – 12x
27x = 96
x =\(\frac{96}{27}\) = 3\(\frac{15}{27}\) = 3\(\frac{5}{9}\)
The length of x is 3\(\frac{5}{9}\) and the length of y is 4\(\frac{5}{9}\).

Exercise 4.
The angle bisector of an angle splits the opposite side of a triangle into lengths 5 and 6. The perimeter of the triangle is 33. Find the lengths of the other two sides.
Answer:
Let z be the scale factor of a similarity. By the angle bisector theorem, the side of the triangle adjacent to the segment of length 5 has length of 5z, and the side of the triangle adjacent to the segment of length 6 has length of 6z. The sum of the sides is equal to the perimeter.
5 + 6 + 5z + 6z = 33
11 + 11z = 33
11z = 22
z = 2
5(2) = 10, and 6(2) = 12 The lengths of the other two sides are 10 and 12.

Eureka Math Geometry Module 2 Lesson 18 Problem Set Answer Key

Question 1.
The sides of a triangle have lengths of 5, 8, and 6\(\frac{1}{2}\). An angle bisector meets the side of length 6\(\frac{1}{2}\). Find the lengths X and y.
Answer:
Using the angle bisector theorem, \(\frac{x}{y}=\frac{5}{8}\) and y = 6 \(\frac{1}{2}\) – x so

Question 2.
The sides of a triangle are 10\(\frac{1}{2}\), 16\(\frac{1}{2}\) and 9. An angle bisector meets the side of length 9. Find the lengths x and y.

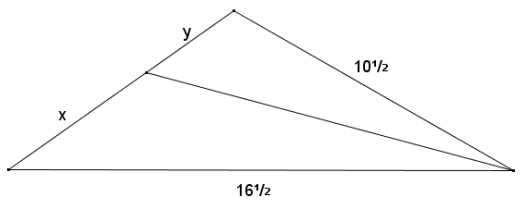
Answer:
By the angle bisector theorem, \(\frac{x}{y}=\frac{16 \frac{1}{2}}{10 \frac{1}{2}}\), and y = 9 – x, so
\(\frac{x}{9-x}=\frac{16.5}{10.5}\)                     y = 9 – x
10.5x = 16.5(9 – x)                  y = 9 – 5.5
10.5x = 148.5 – 16.5x                  y = 3.5
27x = 148.5
x = 5.5

Question 3.
In the diagram of triangle DEF below, \(\overline{D G}\) is an angle bisector, DE = 8, DF = 6, and EF = 8\(\frac{1}{6}\). Find FG and EG.

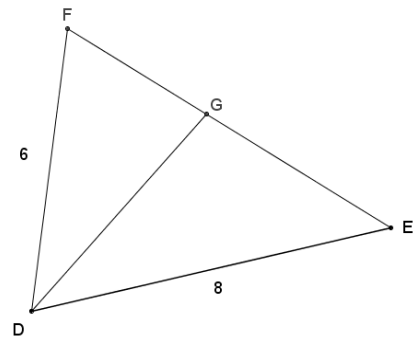
Answer:

Question 4.
Given the diagram below and ∠BAD ≅ ∠DAC, show that BD: BA = CD: CA.

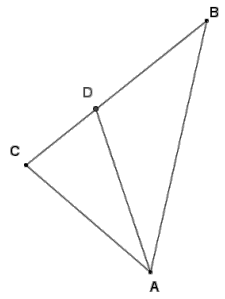
Answer:
Using the given information, Th is the angle bisector of angle A. By the angle bisector theorem, BD : CD = BA : CA, so

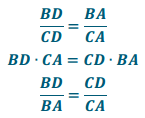
Question 5.
The perimeter of triangle LMN is 32 cm. \(\overline{N X}\) is the angle bisector of angle N, LX = 3 cm, and XM = 5 cm. Find LN and MN.
Answer:
Since \(\overline{N X}\) is an angle bisector of angle N, by the angle bisector theorem, XL: XM = LN: MN; thus, LN: MN = 3: 5.
Therefore, LN = 3x and MN = 5x for some positive number x. The perimeter of the triangle is 32 cm, so
XL + XM + MN + LN = 32
3 + 5 + 3x + 5x = 32
8 + 8x = 32
8x = 24
x = 3
3x = 3(3) = 9 and 5x = 5(3) = 15
LN = 9cm and MN = 15cm

Question 6.
Given CD = 3, DB = 4, BF = 4, FE = 5, AB = 6, and ∠CAD ≅∠DAB ≅ ∠BAF ≅ ∠FAE, find the perimeter of quadrilateral AEBC.

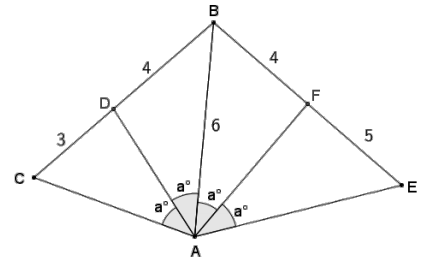
Answer:
\(\overline{A D}\) is the angle bisector of angle CAB, so by the angle bisector theorem, CD: BD = CA: BA.
\(\frac{3}{4}=\frac{C A}{6}\)
4 · CA = 18
CA = 4.5
\(\overline{A D}\) is the angle bisector of angle BAE, so by the angle bisector theorem, BF: EF = BA: EA.
\(\frac{4}{5}=\frac{6}{E A}\)
4 · EA = 30
EA = 7.5
The perimeter of quadrilateral AEBC:
AEBC = CD + DB + BF + FE + EA + AC
AEBC = 3 + 4 + 4 + 5 + 7.5 + 4.5
AEBC = 28

Question 7.
If \(\overline{A E}\) meets \(\overline{B C}\) at D such that CD: BD = CA: BA, show that ∠CAD ≅ ∠BAD. Explain how this proof relates to the angle bisector theorem.

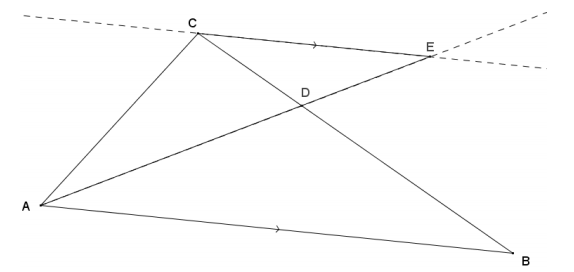
Answer:

Question 8.
In the diagram below, \(\overline{E D}\) ≅ \(\overline{D B}\), \(\overline{B E}\) bisects ∠ABC, AD = 4, and DC = 8. Prove that ∆ ADB ~ ∆ CEB.

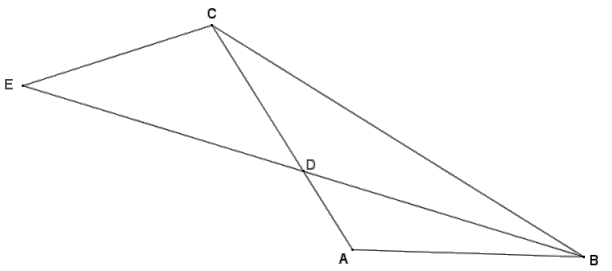
Answer:
Using given information, ED = DB, so it follows that EB = 2DB. Since \(\overline{B E}\) bisects ∠ABC, ∠ABD ≅ ∠CBD. Also, by the angle bisector theorem, \(\frac{C D}{A D}=\frac{B C}{B A}\), which means \(\frac{B C}{B A}=\frac{8}{4}=\frac{2}{1}\).

Since \(\frac{E B}{D B}=\frac{C B}{A B}=\frac{2}{1}\), and ∠ABD ≅ ∠CBD, ∆ ADB ~ ∆ CEB by the SAS criterion for showing similar triangles.

Eureka Math Geometry Module 2 Lesson 18 Exit Ticket Answer Key

Question 1.
The sides of a triangle have lengths of 12, 16, and 21. An angle bisector meets the side of length 21. Find the lengths x and y.

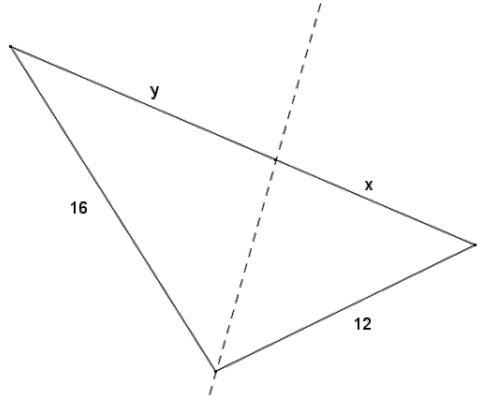
Answer:
By the angle bisector theorem, \(\), and y = 21 – x, so
\(\frac{21-x}{x}=\frac{16}{12}\)                     y = 21 – x
12(21 – x) = 16x                   y = 21 – 9
252 – 12x = 16x                   y = 12
252 = 28x
9 = x

Question 2.
The perimeter of ∆ UVW is 22\(\frac{1}{2}\). \(\overrightarrow{W Z}\) bisects ∠UWV, UZ = 2, and VZ = 2\(\frac{1}{2}\). Find UW and VW.

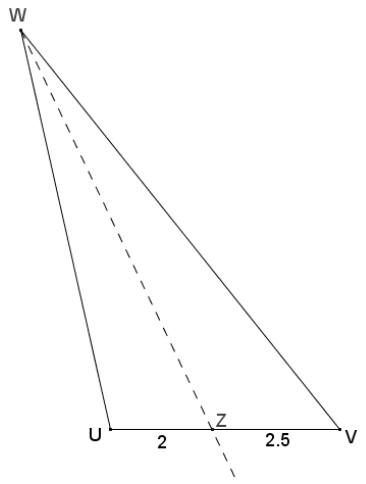
Answer:
By the angle bisector theorem, \(\frac{2}{2.5}=\frac{U W}{V W}\) so UW = 2x and VW = 2. 5x for some positive number x. The perimeter of the triangle is 22\(\frac{1}{2}\), s0
2 + 2.5 + 2x + 2.5x = 22.5
4.5 + 4.5x = 22.5
4.5x = 18
x = 4
UW = 2x = 2(4) = 8
VW = 2.5x = 2.5(4) = 10