Engage NY Eureka Math Geometry Module 2 Lesson 17 Answer Key
Eureka Math Geometry Module 2 Lesson 17 Opening Exercise Answer Key
a. Choose three lengths that represent the sides of a triangle. Draw the triangle with your chosen lengths using construction tools.
Answer:
Answers will vary. Sample response: 6 cm, 7 cm, and 8 cm.
b. Multiply each length in your original triangle by 2 to get three corresponding lengths of sides for a second triangle. Draw your second triangle using construction tools.
Answer:
Answers will be twice the lengths given in part (a). Sample response: 12 cm, 14 cm, and 16 cm.
c. Do your constructed triangles appear to be similar? Explain your answer.
Answer:
The triangles appear to be similar. Their corresponding sides are given as having lengths in the ratio 2: 1, and the corresponding angles appear to be equal in measure. (This can be verified using either a protractor or patty paper.)
d. Do you think that the triangles can be shown to be similar without knowing the angle measures?
Answer:
Answers will vary.
Eureka Math Geometry Module 2 Lesson 17 Exploratory Challenge/Exercise Answer Key
Exercise 1.
Examine the figure, and answer the questions to determine whether or not the triangles shown are similar.
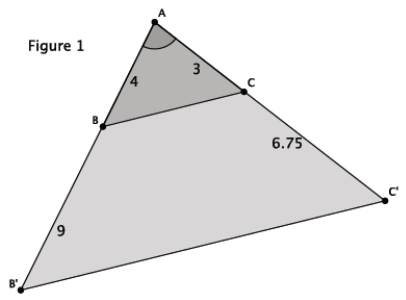
a. What information is given about the triangles in Figure 1?
Answer:
We are given that ∠A is common to both ∆ ABC and ∆ AB’C’. We are also given information about some of the side lengths.
b. How can the information provided be used to determine whether ∆ ABC is similar to ∆ AB’C’?
Answer:
We know that similar triangles will have ratios of corresponding sides that are proportional; therefore, we can use the side lengths to check for proportionality.
c. Compare the corresponding side lengths of ∆ ABC and ∆ AB’C’. What do you notice?
Answer:
\(\frac{4}{13}=\frac{3}{9.75}\)
39 = 39
The cross-products are equal; therefore, the side lengths are proportional.
d. Based on your work in parts (a)-(c), draw a conclusion about the relationship between ∆ ABC and ∆ AB’C’. Explain your reasoning.
Answer:
The triangles are similar. By the triangle side splitter theorem, I know that when the sides of a triangle are cut proportionally, then \(\overline{B C}\) || \(\overline{B^{\prime} C^{\prime}}\). Then, I can conclude that the triangles are similar because they have two pairs of corresponding angles that are equal.
Exercise 2.
Examine the figure, and answer the questions to determine whether or not the triangles shown are similar.
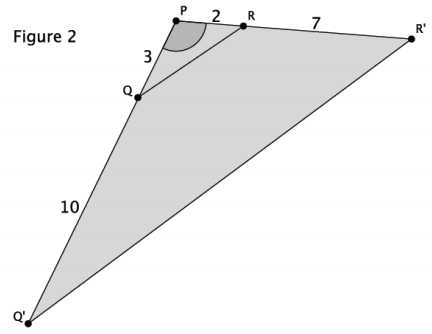
a. What information is given about the triangles in Figure 2?
Answer:
We are given that ∠P is common to both ∆ PQR and ∆ PQ’R’. We are also given information about some of the side lengths.
b. How can the information provided be used to determine whether ∆ PQR is similar to ∆ PQ’R’?
Answer:
We know that similar triangles will have ratios of corresponding sides that are proportional; therefore, we can use the side lengths to check for proportionality.
c. Compare the corresponding side lengths of ∆ PQR and ∆ PQ’R’. What do you notice?
Answer:
\(\frac{3}{13} \neq \frac{2}{9}\)
27 ≠ 26
The side lengths are not proportional.
d. Based on your work in parts (a)-(c), draw a conclusion about the relationship between ∆ PQR and ∆ PQ’R’. Explain your reasoning.
Answer:
The triangles are not similar. The side lengths are not proportional, which is what I would expect in similar triangles. I know that the triangles have one common angle, but I cannot determine from the information given whether there is another pair of equal angles. Therefore, I conclude that the triangles are not similar.
Exercise 3.
Examine the figure, and answer the questions to determine whether or not the triangles shown are similar.
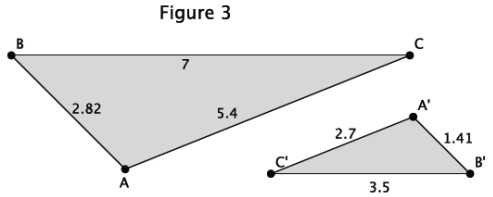
a. What information is given about the triangles in Figure 3?
Answer:
We are only given information related to the side lengths of the triangles.
b. How can the information provided be used to determine whether ∆ ABC is similar to ∆ A’B’C’?
Answer:
We know that similar triangles will have ratios of corresponding sides that are proportional; therefore, we can use the side lengths to check for proportionality.
c. Compare the corresponding side lengths of ∆ ABC and ∆ A’B’C’. What do you notice?
Answer:
\(\frac{1.41}{2.82}=\frac{3.5}{7}=\frac{2.7}{5.4}=\frac{1}{2}\)
The side lengths are proportional.
d. Based on your work in parts (a)-(c), make a conjecture about the relationship between ∆ ABC and ∆ A’B’C’. Explain your reasoning.
Answer:
I think that the triangles are similar. The side lengths are proportional, which is what I would expect in similar triangles.
Exercise 4.
Examine the figure, and answer the questions to determine whether or not the triangles shown are similar.
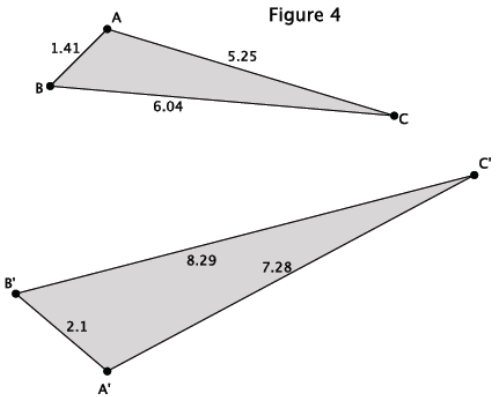
a. What information is given about the triangles in Figure 4?
Answer:
We are only given information related to the side lengths of the triangles.
b. How can the information provided be used to determine whether ∆ ABC is similar to ∆ A’B’C’?
Answer:
We know that similar triangles will have ratios of corresponding sides that are proportional; therefore, we can use the side lengths to check for proportionality.
c. Compare the corresponding side lengths of ∆ ABC and ∆ A’B’C’. What do you notice?
Answer:
\(\frac{2.1}{1.41} \neq \frac{8.29}{6.04} \neq \frac{7.28}{5.25}\)
The side lengths are not proportional.
d. Based on your work in parts (a)-(c), make a conjecture about the relationship between ∆ ABC and ∆ A’B’C’. Explain your reasoning.
Answer:
I think that the triangles are not similar. I would expect the side lengths to be proportional if the triangles were similar.
Exercise 5.
Are the triangles shown below similar? Explain. If the triangles are similar, write the similarity statement.
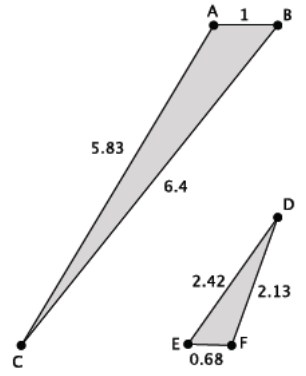
Answer:
\(\frac{1}{0.68} \neq \frac{6.4}{2.42} \neq \frac{5.83}{2.13}\)
There is no information about the angle measures, so we cannot use AA or SAS to conclude the triangles are similar. Since the side lengths are not proportional, we cannot use SSS to conclude the triangles are similar. Therefore, the triangles shown are not similar.
Exercise 6.
Are the triangles shown below similar? Explain. If the triangles are similar, write the similarity statement.
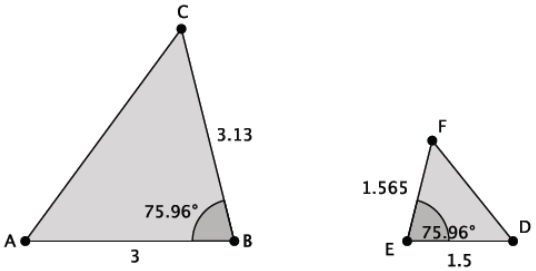
Answer:
\(\frac{3.13}{1.565}=\frac{3}{1.5}\)
Yes, the triangles shown are similar. ∆ ABC ~ ∆ DEF by SAS because m∠B = m∠E, and the adjacent sides are proportional.
Exercise 7.
Are the triangles shown below similar? Explain. If the triangles are similar, write the similarity statement.
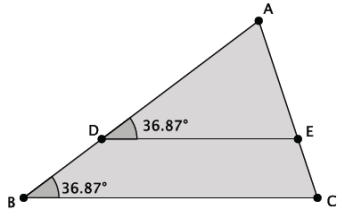
Answer:
Yes, the triangles shown are similar. ∆ ABC ~ ∆ ADE by AA because m∠ADE = m∠ABC, and both triangles share LA.
Exercise 8.
Are the triangles shown below similar? Explain, lithe triangles are similar, write the similarity statement.
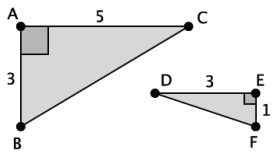
Answer:
\(\frac{5}{3} \neq \frac{3}{1}\)
There is no information about the angle measures other than the right angle, so we cannot use AA to conclude the triangles are similar. We only have information about two of the three side lengths for each triangle, so we cannot use SSS to conclude they are similar. If the triangles are similar, we would have to use the SAS criterion, and since the side lengths are not proportional, the triangles shown are not similar. (Note that students could also utilize the Pythagorean theorem to determine the lengths of the hypotenuses and then use SSS similarity criterion to answer the question.)
Exercise 9.
Are the triangles shown below similar? Explain. If the triangles are similar, write the similarity statement.
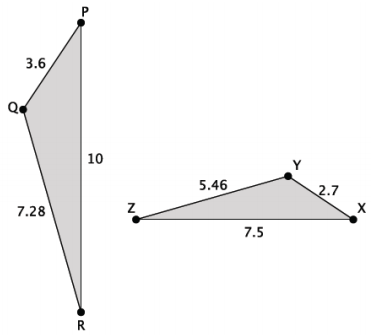
Answer:
\(\frac{3.6}{2.7}=\frac{7.28}{5.46}=\frac{10}{7.5}\)
Yes, the triangles are similar. ∆ PQR ~ ∆ XYZ by SSS.
Exercise 10.
Are the triangles shown below similar? Explain. If the triangles are similar, write the similarity statement.
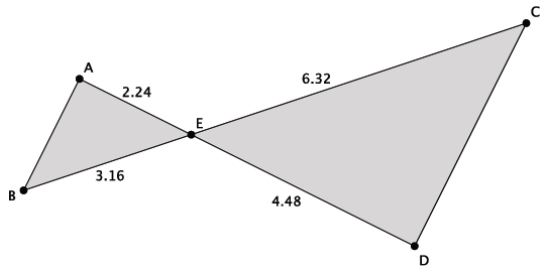
Answer:
\(\frac{2.24}{4.48}=\frac{3.16}{6.32}\)
Yes, the triangles are similar. ∆ ABE ~ ∆ DCE by SAS because m∠AEB = m∠DEC (vertical angles are congruent), and the sides adjacent to those angles are proportional.
Eureka Math Geometry Module 2 Lesson 17 Problem Set Answer Key
Question 1.
For parts (a) through (d) below, state which of the three triangles, if any, are similar and why.
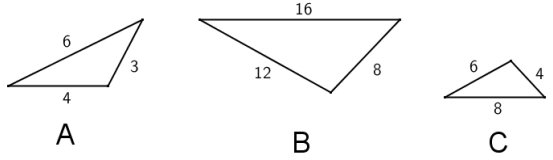
Answer:
Triangles B and C are similar because they share three pairs of corresponding sides that are in the same ratio.
\(\frac{4}{8}=\frac{6}{12}=\frac{8}{16}=\frac{1}{2}\)
Triangles A and B are not similar because the ratios of their corresponding sides are not in the same ratio.
\(\frac{6}{16} \neq \frac{4}{12}\)
Further, if triangle A is not similar to triangle B, then triangle A is not similar to triangle C
b.
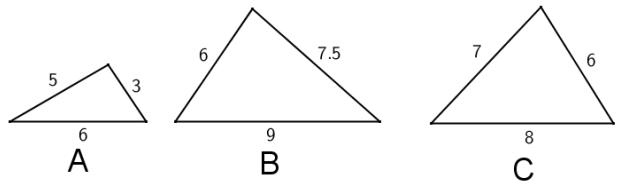
Answer:
Triangles A and B are not similar because their corresponding sides are not oil in the same ratio. Two pairs of corresponding sides are proportional, but the third pair of corresponding sides is not.
\(\frac{3}{6} \neq \frac{5}{7.5}=\frac{6}{9}\)
Triangles B and C are not similar because their corresponding sides are not in the same ratio.
\(\frac{6}{6} \neq \frac{7}{7.5} \neq \frac{8}{9}\)
Triangles A and C are not similar because their corresponding sides are not in the same ratio.
\(\frac{3}{6} \neq \frac{5}{7} \neq \frac{6}{8}\)
c.
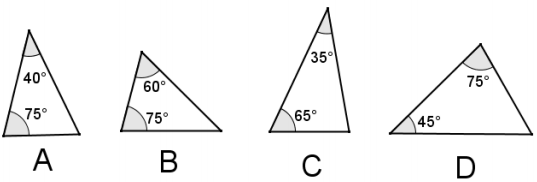
Answer:
Triangles B and D are the only similar triangles because they have the same angle measures. Using the angle sum of a triangle, both triangles B and D have angles of 75°, 60°, and 45°.
d.
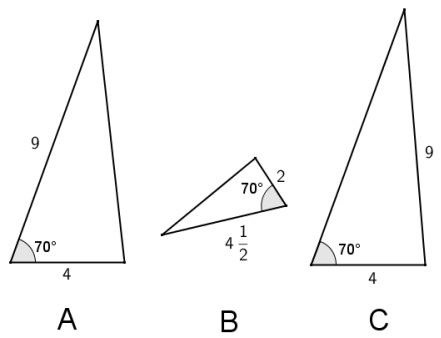
Answer:
Triangles A and B are similar because they have two pairs of corresponding sides that are in the same ratio, and their included angles are equal measures. Triangle C cannot be shown to be similar because, even though it has two sides that are the same length as two sides of triangle A, the 70° angle in triangle C is not the included angle and, therefore, does not correspond to the 70° angle in triangle A.
Question 2.
For each given pair of triangles, determine If the triangles are similar or not, and provide your reasoning. If the triangles are similar, write a similarity statement relating the triangles.
a.
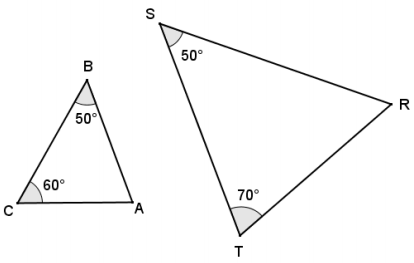
Answer:
The triangles are similar because, using the angle sum of a triangle, each triangle has angle measures of 50°, 60°, and 70°. Therefore, ∆ ABC ~ ∆ TSR.
b.
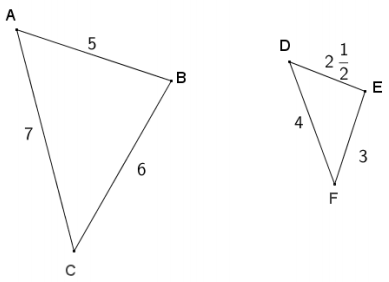
Answer:
The triangles are not similar, because the ratios of corresponding sides are not all in proportion.
\(\frac{A B}{D E}=\frac{B C}{E F}\) = 2; however, \(\frac{A C}{D F}=\frac{7}{4}\) ≠ 2.
c.
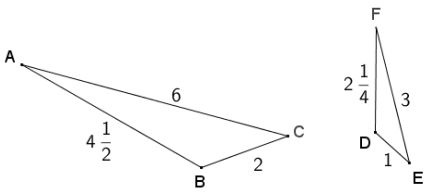
Answer:
∆ ABC ~ ∆ FDE by the SSS criterion for showing similar triangles because the ratio of all pairs of corresponding sides \(\frac{A C}{F E}=\frac{A B}{F D}=\frac{B C}{D E}\) = 2.
d.
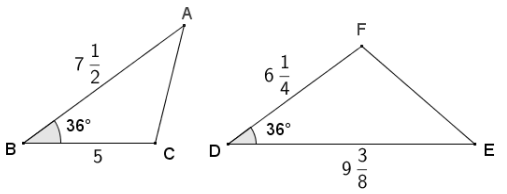
Answer:
\(\frac{A B}{D E}=\frac{B C}{D F}=\frac{4}{5}\), and included angles B and D are both 36° and, therefore, congruent, so ∆ ABC ~ ∆ EDF by the SAS criterion for showing similar triangles.
Question 3.
For each pair of similar triangles below, determine the unknown lengths of the sides labeled with letters.
a.
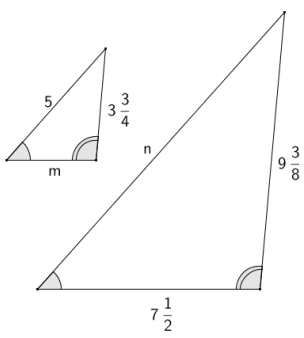
Answer:
The ratios of corresponding sides must be equal, so \(\frac{5}{n}=\frac{3 \frac{3}{4}}{9 \frac{3}{8}}\), giving n = 12\(\frac{1}{2}\). Likewise, \(\frac{m}{7 \frac{1}{2}}=\frac{3 \frac{3}{4}}{9 \frac{3}{8}}\), giving m = 3
b.

Answer:
The ratios of corresponding sides must be equal, so = \(\frac{8}{6}=\frac{s}{6 \frac{3}{4}}\), giving s = 9.
Likewise, = \(\frac{8}{6}=\frac{7}{t}\), giving t = 5\(\frac{1}{4}\).
Question 4.
Given that \(\overline{A D}\) and \(\overline{B C}\) intersect at E and \(\overline{A D}\) || \(\overline{B C}\), show that ∆ ABE ~ ∆ DCE.
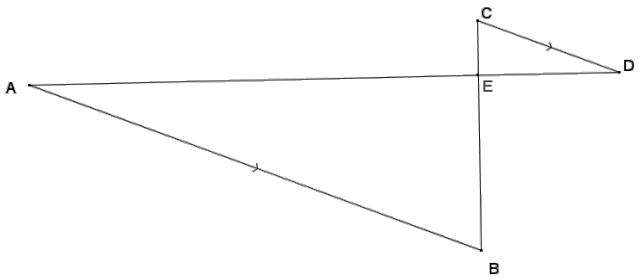
Answer:
∠AEB and ∠DEC are vertically opposite angles and,
therefore, congruent. ∠A ≅ ∠D by alt. int. ∠’s, \(\overline{A D}\) || \(\overline{B C}\). Therefore, ∆ ABE ~ ∆ DCE by the AA criterion for showing similar triangles.
Question 5.
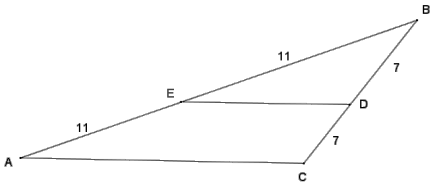
Given BE = 11, EA = 11, BD = 7, and DC = 7, show that ∆ BED ~ t BAC.
Answer:
Both triangles share angle B, and by the reflexive property, ∠B ≅ ∠B. BA = BE + EA, so BA = 22, and BC = BD + DC, so BC = 14. The ratios of corresponding sides \(\frac{B E}{B A}=\frac{B D}{B C}=\frac{1}{2}\). Therefore, ∆ BED ~ ∆ BAC by the SAS criterion for triangle similarity.
Question 6.
Given the diagram below, X is on \(\overline{R S}\) and Y is on \(\overline{R T}\), XS = 2, XY = 6, ST = 9, and YT = 4.
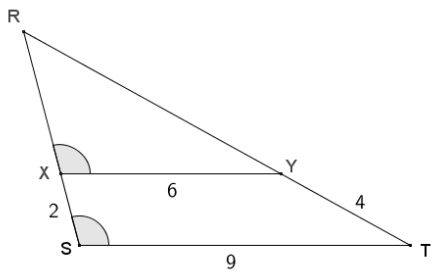
a. Show that ∆ RXY ~ ∆ RST.
Answer:
The diagram shows ∠RST ≅ ∠RXY. Both triangle RXY and RST share angle R, and by the reflexive property, ∠R ≅ ∠R, so ∆ RXY ~ ∆ RST by the AA criterion show triangle similarity.
b. Find RX and RY.
Answer:
Since the triangles are similar, their corresponding sides must be in the same ratio.
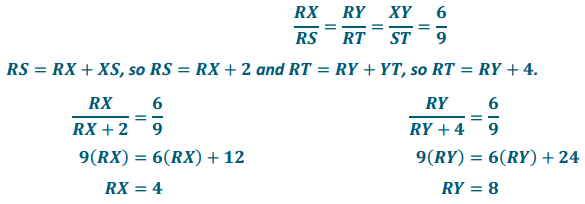
Question 7.
One triangle has a 120° angle, and a second triangle has a 65° angle. Is it possible that the two triangles are similar? Explain why or why not.
Answer:
No The triangles cannot be similar because in the first triangle, the sum of the remaining angles is 60°, which mean that it is not possible for the triangle to have a 65° angle. For the triangles to be similar, both triangles would have to have angles measuring 120° and 65°, but this is impossible due to the angle sum of a triangle.
Question 8.
A right triangle has a leg that is 12 cm, and another right triangle has a leg that is 6 cm. Can you tell whether the two triangles are similar? If so, explain why. If not, what other information would be needed to show they are similar?
Answer:
The two triangles may or may not be similar. There is not enough information to make this claim. If the second leg of the first triangle is twice the length of the second leg of the first triangle, then the triangles are similar by SAS criterion for showing similar triangles.
Question 9.
Given the diagram below, JH = 7. 5, HK = 6, and KL = 9, is there a pair of similar triangles? If so, write a similarity statement, and explain why. If not, explain your reasoning.
Answer:
∆ LKJ ~ ∆ HKL by the SAS criterion for showing triangle similarity. Both triangles share ∠K, and by the reflexive property, ∠K ≅ ∠K. Furthermore, \(\frac{L K}{J K}=\frac{H K}{L K}=\frac{2}{3}\), giving two pairs of corresponding sides in the same ratio and included angles of the same size.
Eureka Math Geometry 2 Module 2 Lesson 17 Exit Ticket Answer Key
Question 1.
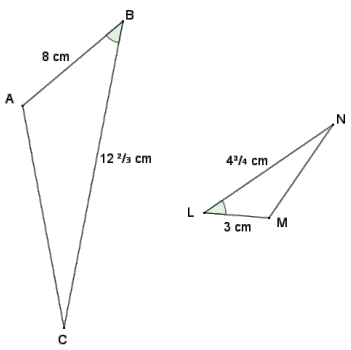
Given ∆ ABC and ∆ MLN in the diagram below, determine if the triangles are similar. If so, write a similarity statement, and state the criterion used to support your claim. B
Answer:
In comparing the ratios of sides between figures, I found that \(\frac{A B}{M L}=\frac{C B}{N L}\) because the cross-products of the proportion \(\frac{8}{3}=\frac{12 \frac{2}{3}}{4 \frac{3}{4}}\) are both 38. We are given that ∠L ≅ ∠B. Therefore, ∆ ABC ~ ∆ MLN by the SAS criterion for proving similar triangles.
Question 2.
Given ∆ DEF and ∆ EGF in the diagram below, determine if the triangles are similar. If so, write a similarity statement, and state the criterion used to support your claim.
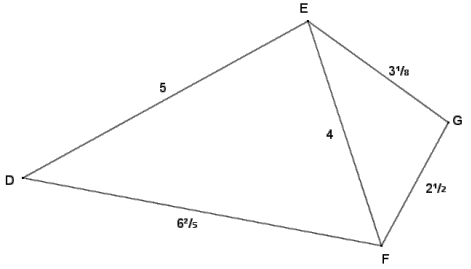
By comparison, if the triangles are in fact similar, then the longest sides of each triangle will correspond, and likewise the shortest sides will correspond. The corresponding sides from each triangle are proportional since
\(\frac{5}{3 \frac{1}{8}}=\frac{4}{2 \frac{1}{2}}=\frac{6 \frac{2}{5}}{4}=\frac{8}{5}\), so \(\frac{D E}{E G}=\frac{E F}{G F}=\frac{D F}{E F}\)
Therefore, by the SSS criterion for showing triangle similarity, ∆ DEF ~ ∆ EGF.