Engage NY Eureka Math Geometry Module 2 Lesson 12 Answer Key
Eureka Math Geometry Module 2 Lesson 12 Example Answer Key
Example 1
Figure Z’ is similar to Figure Z. Describe a transformation that maps Figure Z onto Figure z’.
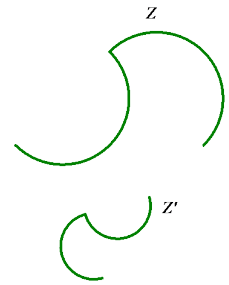
Answer:
→ We are not looking for specific parameters (e.g., scale factor or degree of rotation of each transformation); rather, we want to identify the series of transformations needed to map Figure Z to Figure Z’.
→ Step 1: The dilation has a scale factor of r < 1 since Z’ is smaller than Z.
→ Step 2: Notice that Z’ is flipped from Z1. So, take a reflection of Z1 to get Z2 over a line 1.
→ Step 3: Translate the plane such that a point of Z2 maps to a corresponding point in Z’. Call the new figure Z3.
→ Step 4: Rotate until Z3 coincides with Z’.
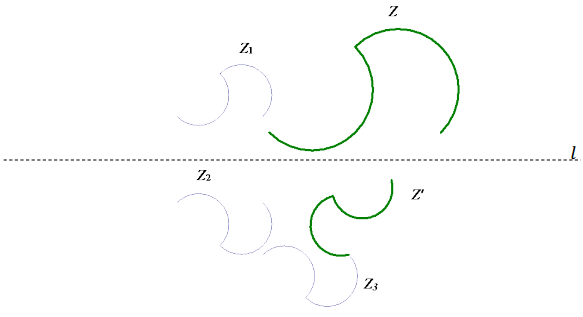
Figure Z maps to Figure Z’ by first dilating by a scale factor of r until the corresponding lengths are equal in measurement and then reflecting over line I to ensure that both figures have the same orientation. Next, translate along a vector so that one point of the image corresponds to Z’. Finally, a rotation around a center C of degree θ orients Figure Z so that it coincides with Figure Z’.
Example 2.
Show that no sequence of basic rigid motions and dilations takes the small figure to the large figure. Take measurements as needed.
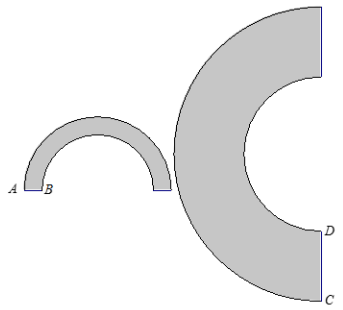
Answer:
A similarity transformation that maps the small outer circle to the large outer circle would need to have scale factor of about 2. A similarity transformation that maps the small line segment AB to the large line segment CD would need to have scale factor of about 4. So, there is no similarity transformation that maps the small figure onto the large figure.
Eureka Math Geometry Module 2 Lesson 12 Opening Exercise Answer Key
Observe Figures 1 and 2 and the images of the intermediate figures between them. Figures 1 and 2 are called similar.
What observations can we make about Figures 1 and 2?

Answer:
Answers will vary; students might say that the two figures look alike in terms of shape but not size. Accept reasonable answers at this point to start the conversation, and move on to filling out the chart below.
Definition:
A __________ ___________ (or ) ___________) is a composition of a finite number of dilations or basic rigid motions. The scale factor of a similarity transformation is the product of the scale factors of the dilations in the composition. If there are no dilations in the composition, the scale factor is defined to be 1.
Answer:
Similarity transformation, similarity
Definition:
Two figures in a plane are _____________ if there exists a similarity transformation taking one figure onto the other figure.
Answer:
Similar
Answer:
Eureka Math Geometry Module 2 Lesson 12 Exercise Answer Key
Exercise 1.
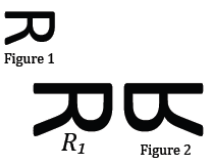
Figure 1 is similar to Figure 2. Which transformations compose the similarity transformation that maps Figure 1 onto Figure 2?
Answer:
First, dilate Figure 1 by a scale factor of r > 1 until the corresponding lengths are equal in measurement, and then reflect over a line iso that Figure 1 coincides with Figure 2.
Exercise 2.
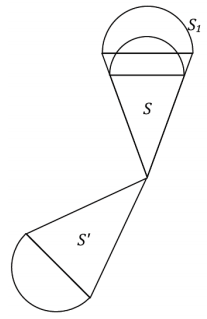
Figure S is similar to Figure S’. Which transformations compose the similarity transformation that maps S onto S’?
Answer:
First, dilate S by a scale factor of r > 1 until the corresponding segment lengths are equal in measurement to those of S’. Then, S must be rotated around a center C of degree θ so that S coincides with S’.
Exercise 3.
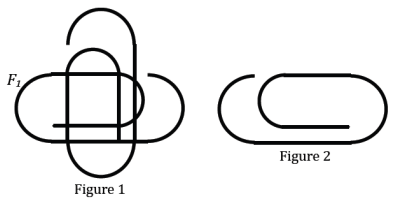
Figure 1 is similar to Figure 2. Which transformations compose the similarity transformation that maps Figure 1 onto Figure 2?
Answer:
It is possible to only use two transformations: a rotation followed by a reflection. However, to do this, the correct center must be found. The solution image reflects this approach, but students may say to first rotate Figure 1 around a center C by 90° in the clockwise direction. Then, reflect Figure 1 over a vertical line t. Finally, translate Figure 1 by a vector so that Figure 1 coincides with Figure 2.
Exercise 4.
Is there a sequence of dilations and basic rigid motions that takes the large figure to the small figure? Take measurements as needed.
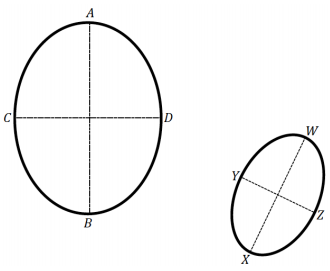
Answer:
A similarity transformation that maps segment AB to segment WX would need to have scale factor of about \(\frac{2}{3}\), but a similarity transformation that maps the small segment CD to segment YZ would need to have scale factor of about \(\frac{1}{2}\). So, there is no similarity transformation that maps the large figure onto the small figure.
Exercise 5.
What purpose do transformations serve? Compare and contrast the application of rigid motions to the application of similarity transformations.
Answer:
We use all the transformations to compare figures in the plane. Rigid motions are distance preserving while dilations, integral to similarity transformations, are not distance preserving. We use compositions of rigid motions to determine whether two figures are congruent, and we use compositions of rigid motions and dilations, specifically similarity transformations, to determine whether figures are similar.
Eureka Math Geometry Module 2 Lesson 12 Problem Set Answer Key
Question 1.
What is the relationship between scale drawings, dilations, and similar figures?
a. How are scale drawings and dilations alike?
Answer:
Scale drawings and dilated figures are alike in that all corresponding angles are congruent and all corresponding distances are in the equivalent ratio, r, called the scale factor. A dilation of a figure produces a scale drawing of that figure.
b. How can scale drawings and dilations differ?
Answer:
Dilations are a transformation of the plane in which all corresponding points from the image and pre-image are mapped along rays that originate at the center of dilation. This is not a requirement for scale drawings.
c. What is the relationship of similar figures to scale drawings and dilations?
Answer:
Similar figures are scale drawings because they can be mapped together by a series of dilations and rigid motions.
Question 2.
Given the diagram below, identify a similarity transformation, if one exists, that maps Figure A onto Figure B. If one does not exist, explain why.
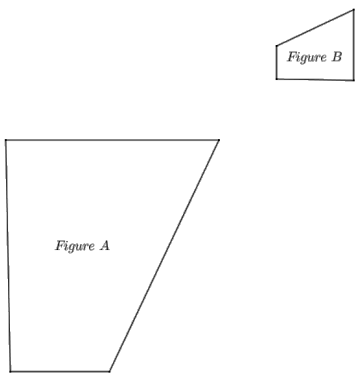
Answer:
(Note to the teacher: The solution below is only one of many valid solutions to this problem.)
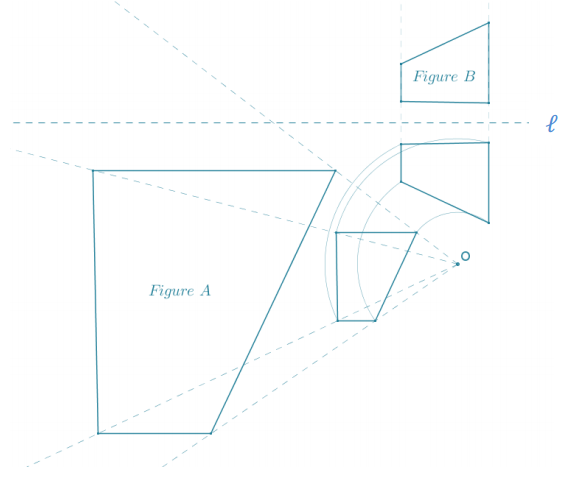
Question 3.
Teddy correctly identified a similarity transformation with at least one dilation that maps Figure I onto Figure II. Megan correctly identified a congruence transformation that maps Figure I onto Figure II. What must be true about Teddy’s similarity transformation?
Answer:
If Megan correctly identified a congruence transformation that maps Figure I onto Figure II, then Figure 1 and Figure II must be congruent. Therefore, Teddy’s similarity transformation must have either included a single dilation with a scale factor of 1 or must have included more than one dilation of which the product of all scale factors was 1 because it included at least one dilation.
Question 4.
Given the coordinate plane shown, identify a similarity transformation, if one exists, that maps X onto Y. If one does not exist, explain why.
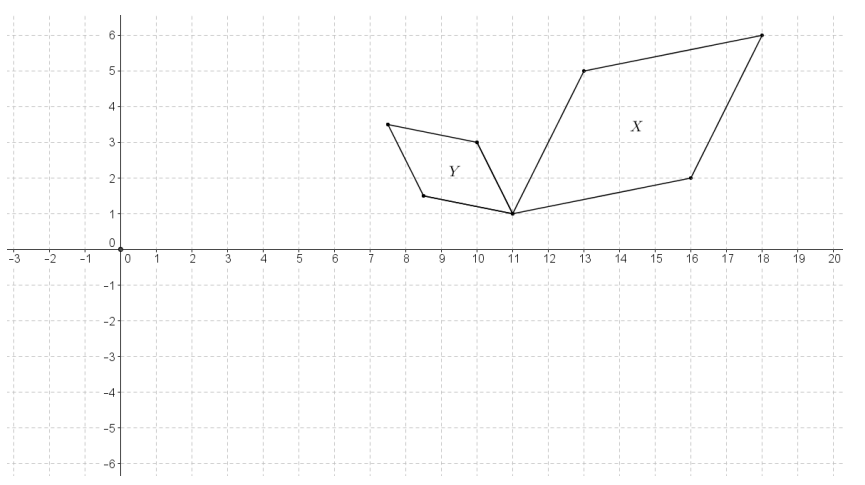
Answer:
(Note to the teacher: The solution below is only one of many valid solutions to this problem.)
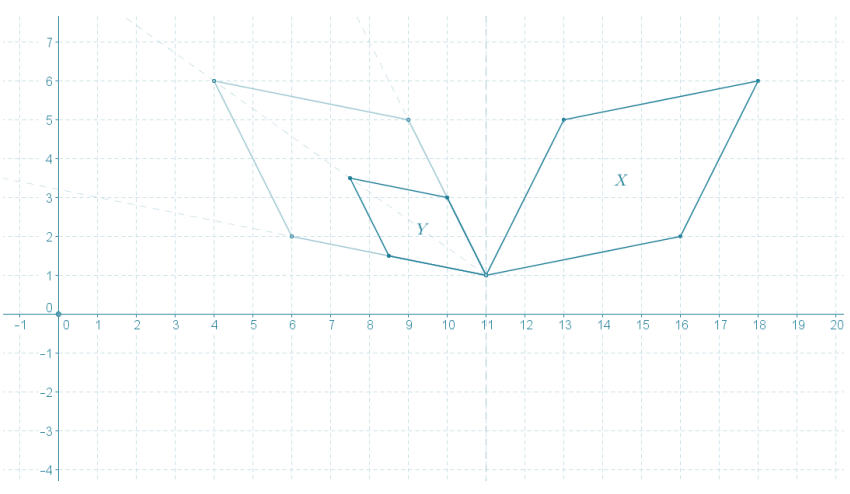
First, reflect X over line x = 11. Then, dilate the image from center (11, 1) with a scale factor of \(\frac{1}{2}\) to obtain Y.
Question 5.
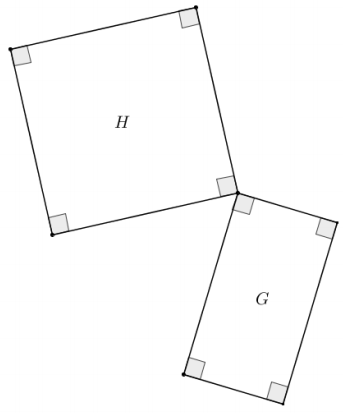
Given the diagram below, identify a similarity transformation, if one exists, that maps G onto H. If one does not exist, explain why. Provide any necessary measurements to justify your answer.
Answer:
A similarity transformation does not exist that maps G onto H because the side lengths of the figures are not all proportional. Figure G Is a rectangle (not a square), whereas Figure H is a square.
Question 6.
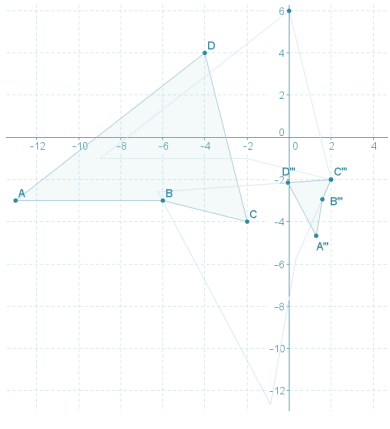
Given the coordinate plane shown, identify a similarity transformation, if one exists, that maps ABCD onto A”’B”’C”’D”’. If one does not exist, explain why.
Answer:
(Note to the teacher: Students need to use a protractor to obtain the correct degree measure of rotation. The solution below Is only one of many valid solutions to this problem.)
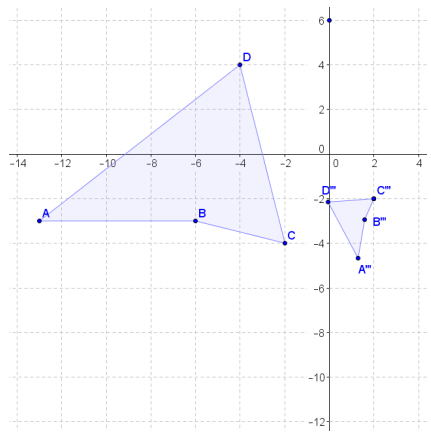
ARCD can be mapped onto A”’B”’C”’D”’ by first translating along the vector \(\overrightarrow{C C^{\prime \prime \prime}}\), then rotating about point C” by 80°, and finally dilating from point C” using a scale factor of \(\frac{1}{4}\).
Question 7.
The diagram below shows a dilation of the plane … or does it? Explain your answer.
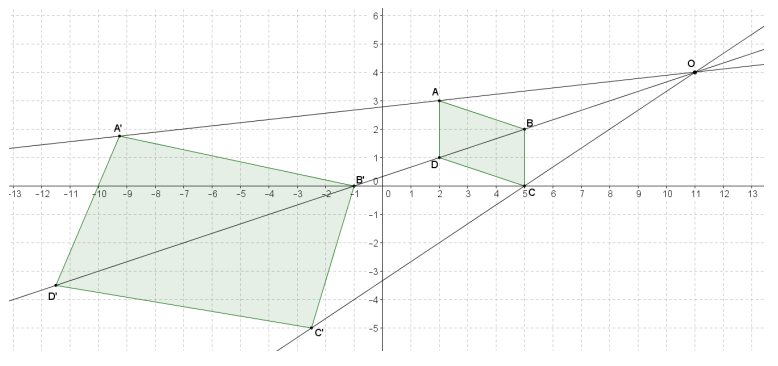
Answer:
The diagram does not show a dilation of the plane from point O, even though the corresponding points are collinear with the center O. To be a dilation of the plane, a constant scale factor must be used for all points from the center of dilation; however, the scale factor relating the distances from the center in the diagram range from 2 to 2.5.
Eureka Math Geometry Module 2 Lesson 12 Exit Ticket Answer Key
Question 1.
Figure A’ is similar to Figure A. Which transformations compose the similarity transformation that maps Figure A onto Figure A’?
Answer:
One possible solution: We first take a dilation of Figure A with a scale factor of r < 1 and center O, the point where the two line segments meet, until the corresponding lengths are equal to those in Figure A Next, take a rotation (180°) about O, and then, finally, take a reflection over a (vertical) line t.
Question 2.
Is there a sequence of dilations and basic rigid motions that takes the small figure to the large figure? Take measurements as needed.

Answer:
No similarity transformation exists because the circled corresponding distances and the corresponding distances marked by the arrows on Figure B are not in the same ratio.