Eureka Math Geometry Module 2 Lesson 10 Answer Key

Engage NY Eureka Math Geometry Module 2 Lesson 10 Answer Key

Eureka Math Geometry Module 2 Lesson 10 Opening Exercise Answer Key

Use a compass to mark off equally spaced points C, D, E, and F so that AB, BC, CD, DE, and EF are equal in length. Describe the steps you took.
$Eureka Math Geometry Module 2 Lesson 10 Exercise Answer Key 1$
I adjust the compass to the length of Ã and then place the point of the compass on B and use the adjustment to make a mark so that it intersects with the ray. This is the location of C, and i repeat these steps until I locate point F.
$Eureka Math Geometry Module 2 Lesson 10 Exercise Answer Key 2$

Eureka Math Geometry Module 2 Lesson 10 Exercise Answer Key

Exercise 1.
Divide segment AB into five segments of equal lengths.
$Eureka Math Geometry Module 2 Lesson 10 Exercise Answer Key 3$
Answer:
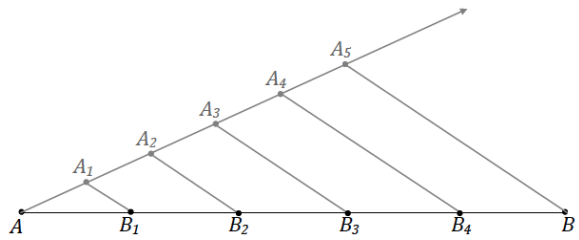
$Eureka Math Geometry Module 2 Lesson 10 Exercise Answer Key 4$

Exercise 2.
On a piece of poster paper, draw a segment AB with a measurement of 1 foot. Use the dilation method to divide Ã into twelve equal-length segments, or into 12 inches.
Answer:
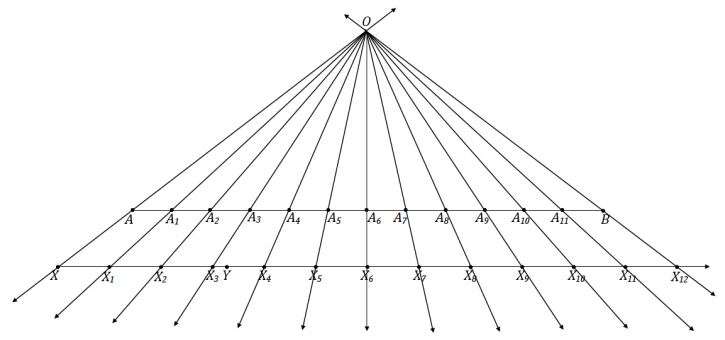
$Eureka Math Geometry Module 2 Lesson 10 Exercise Answer Key 5$

Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key

Question 1.
Pretend you are the king or queen and that the length of your foot is the official measurement for one foot. Draw a line segment on a piece of paper that is the length of your foot. (You may have to remove your shoe.) Use the method above to find the length of 1 inch in your kingdom.
Answer:
I drew $\overline{A B}$ representing the length of my foot. I then divided $\overline{A B}$ into twelve equal pieces using the dilation method as follows:

I constructed $\overleftrightarrow{D E}$ parallel to $\overline{A B}$ and, using a compass, marked off twelve consecutive segments on $\overleftrightarrow{D E}$ each having length DC. (Note that because $\overline{A B}$ is a large segment, students will likely choose a length DC so that the total length of all of the segments constructed on $\overleftrightarrow{D E}$ is noticeably shorter than AB.)

I then constructed a ray from A and B through the endpoints of the composed segment, as shown in the diagram, to form a triangle ABO. Next, I constructed $\overrightarrow{O C}$, and then i marked its intersection with $\overline{A B}$ point I. This distance AI is the length of 1 inch in my kingdom.
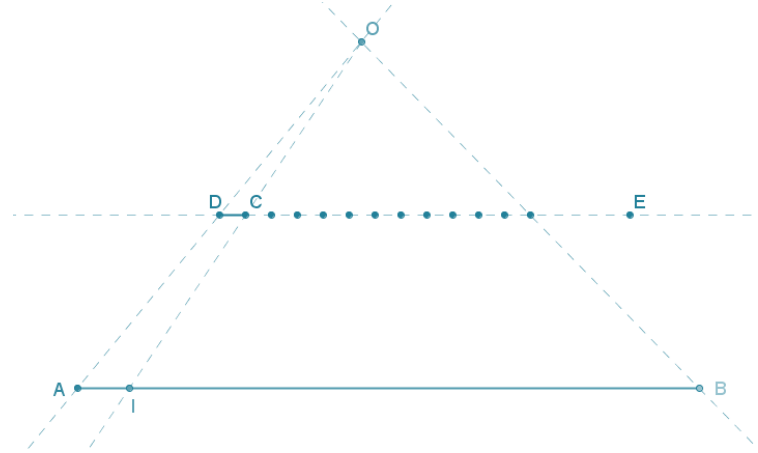
$Eureka Math Geometry Module 2 Lesson 10 Exercise Answer Key 6$

Question 2.
Using a ruler, draw a segment that is 10 cm. This length is referred to as a decimeter. Use the side splitter method to divide your segment into ten equal-sized pieces. What should be the length of each of those pieces based on your construction? Check the length of the pieces using a ruler. Are the lengths of the pieces accurate?
Answer:
Verify that students’ diagrams show the use of the side splitter method. The length of each piece should be 1 cm.

Question 3.
Repeat Problem 2 using the dilation method. What should be the length of each of those pieces based on your construction? Check the lengths of the pieces using a ruler. Are the lengths of the pieces accurate?
Answer:
Verify that students’ diagrams show the use of the dilation method. The length of each piece should be 1 cm.

Question 4.
A portion of a ruler that measured whole centimeters Is shown below. Determine the location of 5$\frac{2}{3}$ cm on the portion of the ruler shown.
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 7$
Answer:
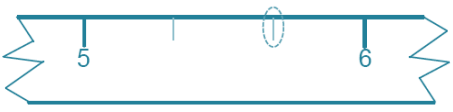
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 8$
Responses should show the segment between 5 and 6 divided into 3 equal pieces with the division point closest to 6 chosen as the location of 5$\frac{2}{3}$.

Question 5.
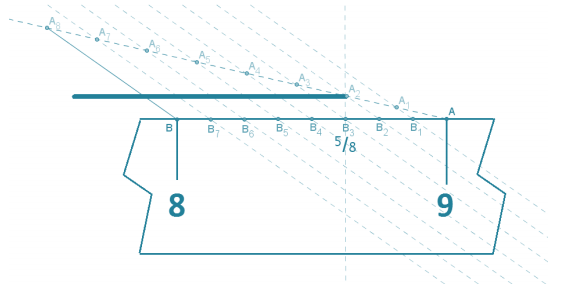
Merrick has a ruler that measures In inches only. He is measuring the length of a line segment that is between 8 in. and 9 in. Divide the one-inch section of Merrick’s ruler below into eighths to help him measure the length of the segment.
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 9$
Answer:
Using the side splitter method, I divided the one-inch interval into eighths, labeled as B₁, B₂, etc., on the diagram. The line segment that Merrick is measuring closely corresponds with B₃, which represents of the $\frac{5}{8}$ distance from 8 in. to 9 in. Therefore, the length of the line segment that Merrick is measuring is approximately 8$\frac{5}{8}$ in.
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 10$

Question 6.
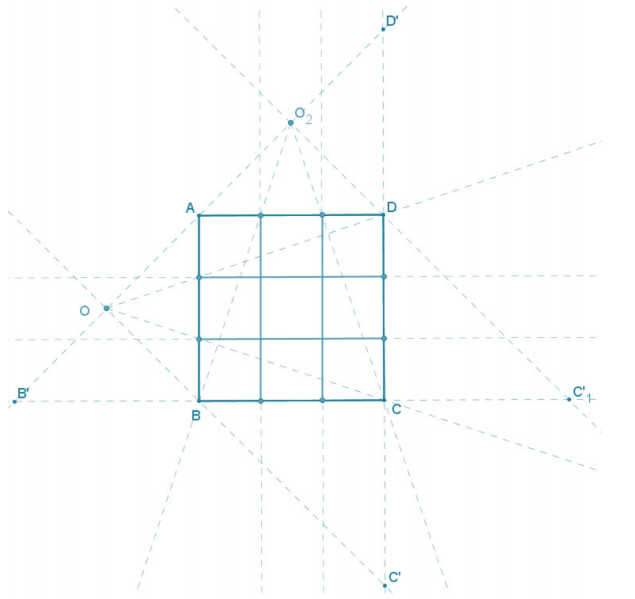
Use the dilation method to create an equally spaced 3 × 3 grid in the following square.
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 11$
Answer:
There are several ways to complete this construction. The sample below used the dilation method along two sides of the square with centers O and O₂ to divide the side into three equal-size segments. The sides of the square were extended such that DD’ = CD, CC’ = CD, BR’ = CB, and CC’₁ = CB.
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 12$

Question 7.
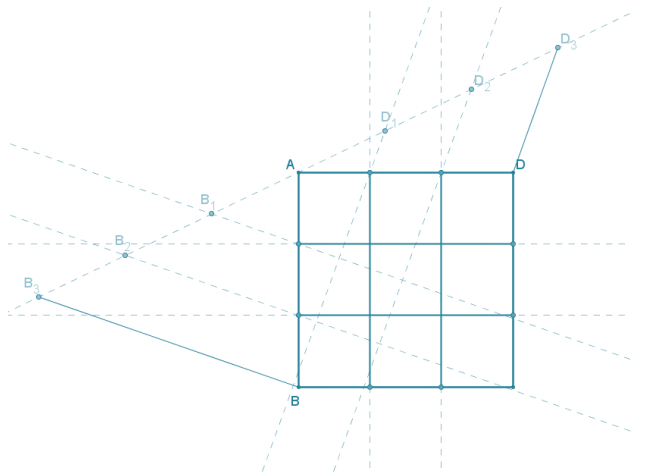
Use the side splitter method to create an equally spaced 3 × 3 grid In the following square.
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 13$
Answer:
There are several ways to complete this construction. The sample below used the side splitter method along two sides of the square to divide the side into three equal-size segments.
$Eureka Math Geometry Module 2 Lesson 10 Problem Set Answer Key 14$

Eureka Math Geometry Module 2 Lesson 10 Exit Ticket Answer Key

Question 1.
Use the side splitter method to divide $\overline{M N}$ into 7 equal-sized pieces.
Answer:
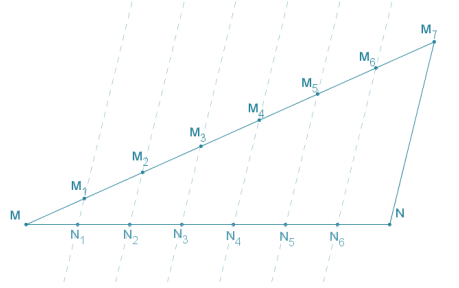
$Eureka Math Geometry Module 2 Lesson 10 Exit Ticket Answer Key 15$

Question 2.
Use the dilation method to divide $\overline{P Q}$ into 11 equal-sized pieces.
Answer:
$Eureka Math Geometry Module 2 Lesson 10 Exit Ticket Answer Key 16$

Question 3.
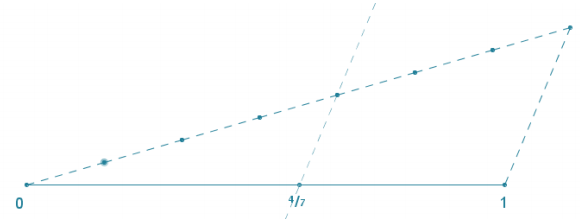
If the segment below represents the interval from zero to one on the number line, locate and label $\frac{4}{7}$.
$Eureka Math Geometry Module 2 Lesson 10 Exit Ticket Answer Key 17$
Answer:
Students may use either the side splitter method or the dilation method and need only find the location of the fourth equal-sized piece of the segment, as shown in the diagram below.
$Eureka Math Geometry Module 2 Lesson 10 Exit Ticket Answer Key 18$

Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key

Question 1.
Divide segment AB into three segments of equal lengths.
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 19$
Answer:
Draw each step of the Exploratory Challenge so that students can refer to the correct steps whether they are ahead or
working alongside the teacher.
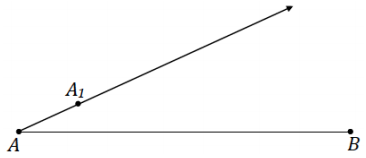
→ Pick a point A₁ not on $\overline{A B}$. Draw $\overrightarrow{A A_{1}}$.
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 20$

→ Mark points A₂ and A₃ on the ray so that AA₁ = AA₂ = A₂A₃.
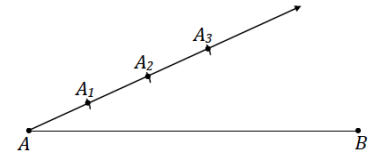
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 21$

→ Use a straightedge to draw $\overline{A_{3} B}$. Use a set square to draw segments parallel to $\overline{A_{3} B}$ through A₁ and A₂.
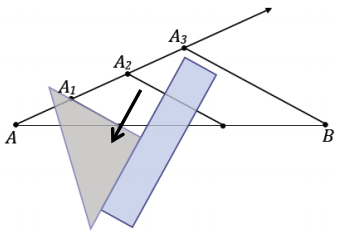
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 22$

→ Label the points where the constructed segments intersect $\overline{A B}$ as B₁ and B₂.
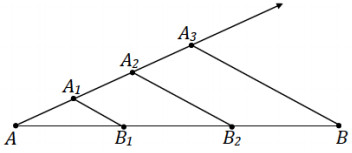
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 23$

Allow students time to discuss with each other why the construction divides AB into equal parts.
→ Did we succeed? Measure segments AB₁, B₁B₂, and B₂B. Are they all equal in measurement?
→ After the last step of the construction, answer the following: Why does this construction divide the segment AB into equal parts?

Allow students a moment to jot down their thoughts, and then take responses.
→ By construction, segments A₁B₁ and A₂B₂ are parallel to segment A₃B₃. By the triangle side splitter theorem, $\overline{A_{1} B_{1}}$ and $\overline{A_{2} B_{2}}$ are proportional side splitters of triangle ABA₃. So, $\frac{A B_{1}}{A B}=\frac{A A_{1}}{A A_{3}}=\frac{1}{3}$ and $\frac{A B_{2}}{A B}=\frac{A A_{2}}{A A_{3}}=\frac{2}{3}$. Thus, AB₁ = $\frac{1}{3}$AB and AB₂ = $\frac{2}{3}$AB, and we can conclude that B₁ and B₂ divide line segment AB into three equal pieces.

Question 2.
Divide segment AB into four segments of equal length.
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 24$
Answer:
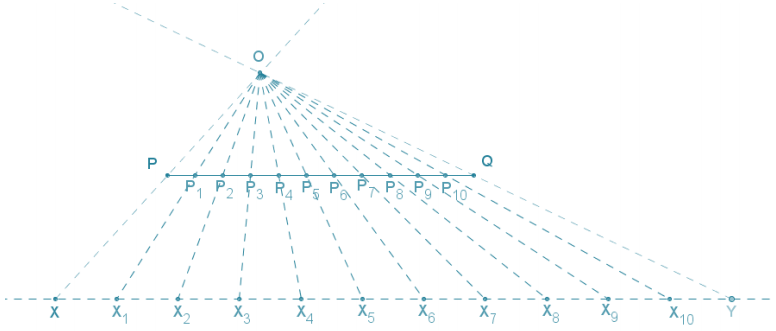
→ Use the set square to create a ray XY parallel to $\overline{A B}$. Select the location of the endpoint X so that it falls to the left of A; the location of Y should be oriented in relation to X in the same manner as B is in relation to A. We construct the parallel ray below $\overline{A B}$, but it can be constructed above the segment as well.
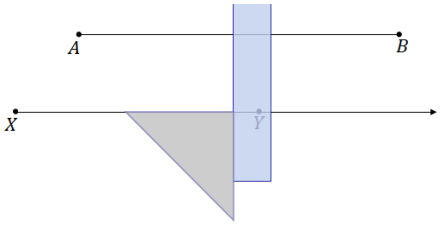
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 25$

→ From X, use the compass to mark off four equal segments along $\overrightarrow{X Y}$. Label each intersection as X₁, X₂, X₃, and X₄. It is important that XX₄ ≠ AB. In practice, XX₄ should be clearly more or clearly less than AB.
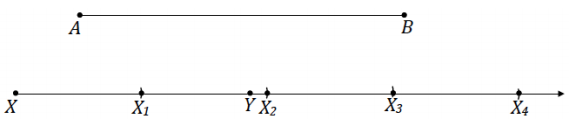
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 26$

→ Draw line XA and line X₄B. Mark the intersection of the two lines as O.
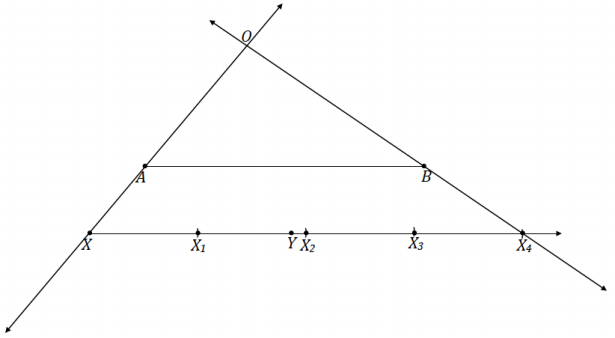
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 27$

→ Construct rays from O through X₁, X₂, and X₃. Label each intersection with $\overline{A B}$ as A₁, A₂, and A₃.
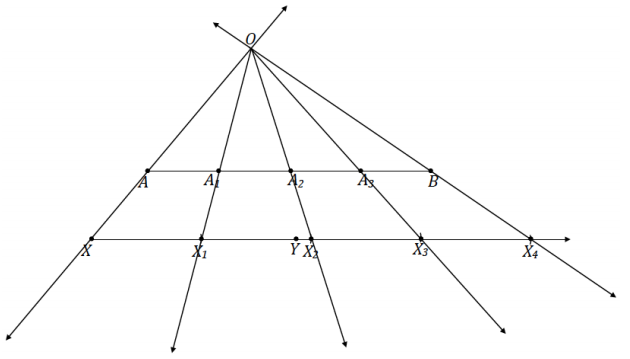
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 28$

→ $\overline{A B}$ should now be divided into four segments of equal length. Measure segments AA₁, A₁A₂, A₂A₃, and A₃B. Are they all equal in measurement?

→ Why does this construction divide the segment AB into equal parts?

Allow students time to discuss with each other why the construction divides $\overline{A B}$ into equal parts.

We constructed $\overline{A B}$ to be parallel to $\overrightarrow{X Y}$. In ∆ X OX4, since the side splitter $\overline{A B}$ is parallel to $\overline{X X_{4}}$, by the triangle side splitter theorem, it must also be a proportional side splitter. By the dilation theorem, this means that $\frac{A A_{1}}{X X_{1}}=\frac{A_{1} A_{2}}{X_{1} X_{2}}=\frac{A_{2} A_{3}}{X_{2} X_{3}}=\frac{A_{3} B}{X_{3} X_{4}}$. Since we know that the values of all four denominators are the same, the value of all four numerators must also be the same to make the equation true.
Therefore, $\overline{A B}$ has been divided into four segments of equal length.

→ We call this method of dividing the segment into equal lengths the dilation method, as the points that divide $\overline{A B}$ are by definition dilated points from center O with scale factor r = $\frac{O A}{O X}$ of the evenly spaced points on $\overrightarrow{X Y}$.

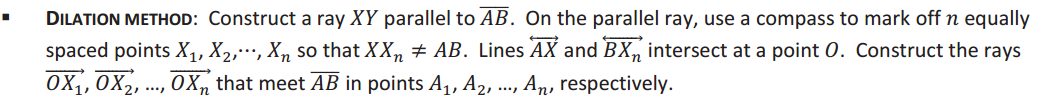
$Eureka Math Geometry Module 2 Lesson 10 Exploratory Challenge Answer Key 29$

→ What happens if line segments XX and AB are close to the same length?
The point O is very far away.

→ That is why it is best to make XX_n clearly more or less than AB. It is also best to keep line segments XX_n and AB centered, or the point O will also be far away.