Engage NY Eureka Math Geometry Module 1 Lesson 34 Answer Key
Eureka Math Geometry Module 1 Lesson 34 Review Exercise Answer Key
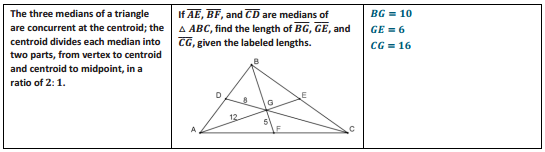
Review Exercise:
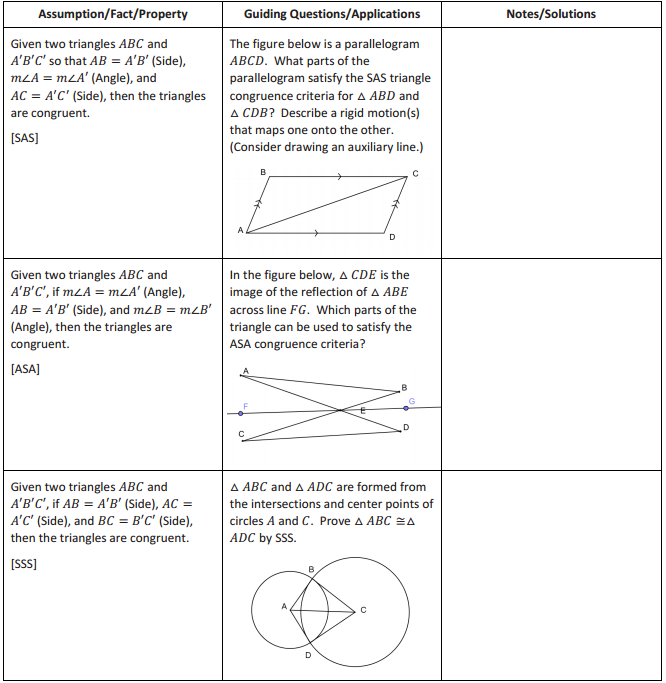
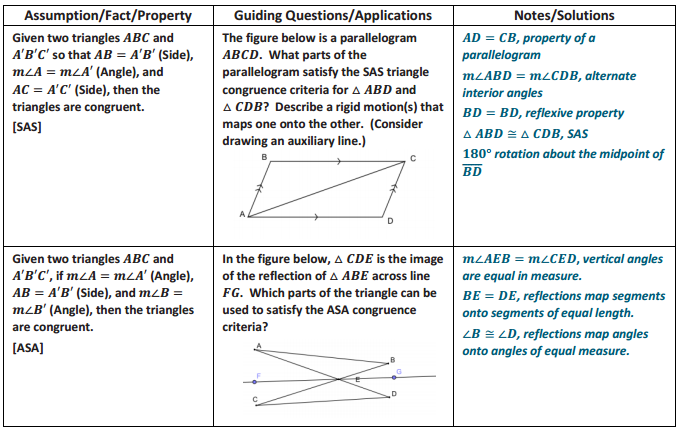
Answer:
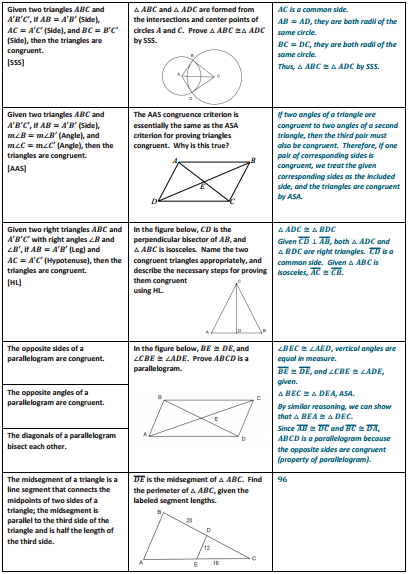
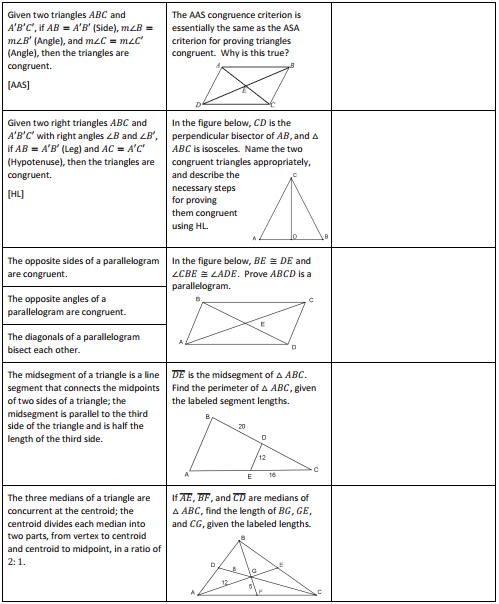
Eureka Math Geometry Module 1 Lesson 34 Problem Set Answer Key
Use any of the assumptions, facts, and/or properties presented in the tables above to find x and/or y in each figure below. Justify your solutions.
Question 1.
Find the perimeter of parallelogram ABCD. Justify your solution.
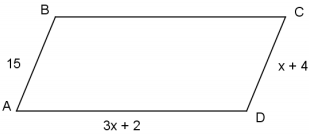
Answer:
100, 15 = x + 4, x = 11
Question 2.
AC = 34
AB = 26
BD = 28
Given parallelogram ABCD, find the perimeter of CED. Justify your solution.
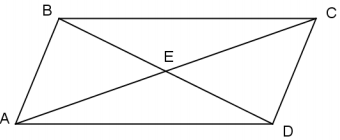
Answer:
57
CE = \(\frac{1}{2}\)AC; CE = 17
CD = AB; CE = 26
ED = \(\frac{1}{2}\)BD; ED = 14
Perimeter = 17 + 26 + 14 = 57
Question 3.
XY = 12
XZ = 20
ZY = 24
F, G, and H are midpoints of the sides on which they are located. Find the perimeter of FGH. Justify your solution.
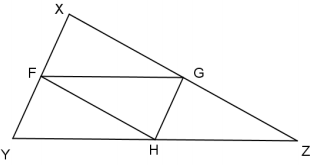
Answer:
28
The midsegment is half the length of the side of the triangle it is parallel to.
Question 4.
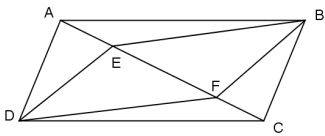
ABCD is a parallelogram with AE = CF. Prove that DEBF is a parallelogram.
Answer:
AE = CF – Given
AD = BC – Property of a parallelogram
m∠DAE = m∠BCF – If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
∆ADE ≅ ∆CBF – SAS
DE = BF – Corresponding sides of congruent triangles are congruent.
AB = DC – Property of a parallelogram
m∠BAE = m∠DCF – If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
∆BAE ≅ ∆DCF – SAS
BE = DF – Corresponding sides of congruent triangles are congruent.
∴ ABCD is a parallelogram. – If both sets of opposite sides of a quadrilateral are equal in length, then the quadrilateral is a parallelogram.
Question 5.
C is the centroid of RST. RC = 16. CL = 10. TJ = 21
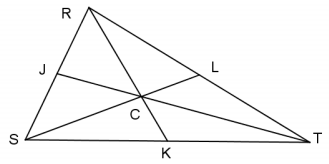
SC = __
TC = __
KC = __
Answer:
SC = 20
TC = 14
KC = 8
Eureka Math Geometry Module 1 Lesson 34 Exit Ticket Answer Key
Question 1.
The inner parallelogram in the figure is formed from the midsegments of the four triangles created by the outer parallelogram’s diagonals. The lengths of the smaller and larger midsegments are as indicated. If the perimeter of the outer parallelogram is 40, find the value of x.
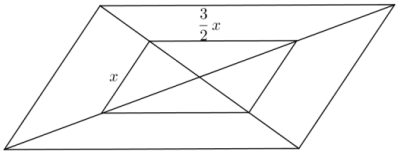
Answer:
x = 4